Determination of the Planck’s constant and the output work from the experimental data for Photoelectric effect
Task number: 4382
From the following values measured during the external photoelectric effect on lithium determine the Planck’s constant and the output work for lithium. Compare the obtained values with the table values.
| radiation wavelength λ [nm] | 433.9 | 404.7 | 365.0 | 312.5 | 253.5 |
| stopping voltage U [V] | 0.55 | 0.73 | 1.09 | 1.67 | 2.57 |
Hint
In order to solve this problem it is necessary to know the Einstein’s equation for photoelectric effect which determines the maximum kinetic energy Ek of emitted electrons
\[E_k=hf-W_v ,\]where the product of the Planck’s constant h and the radiation frequency f is equal to the energy of one a landing photon and Wv is the so-called output work (constant characterizing the used metal).
This equation tells us that there is a linear relation between the radiation frequency and the maximum kinetic energy of the emitted electrons. Therefore the easiest way to solve this would be to calculate frequencies from the wavelengths and kinetic energies from the stopping voltage, plot the values, fit the data with the linear fit and from its equation determine the desired constants.
Fitting of the plot – linear regression – can be done with paper and a calculator but we can also use some program for it such as MS Excel.
Analysis
During the photoelectric effect we observe that if the light (in general electromagnetic radiation) lands on a metal, it can emit electrons from the metal which creates the so-called photoelectric current during certain conditions. This effect was described by A. Einstein who also put together the Einstein’s equation for the photoelectric effect that determines the maximum kinetic energy Ek of emitted electrons.
Maximum kinetic energy of the electrons is measured with stopping voltage, i.e. measurement of the voltage which the electrons cannot overcome. The work done by the electric forces when the electron is passing through that voltage equals to the kinetic energy of the electron being released from the metal.
The output work and Planck’s constant in this law can be determined by comparing the measured data and the theoretical formula.
Solution
The Einstein’s equation of photoelectric effect that determines the maximum kinetic energy Ek of emitted electrons is stated as follows
\[E_k=hf-W_v ,\]where the product of the Planck’s constant h and the radiation frequency f is equal to the energy of one landing photon and Wv is the so-called output work (constant characterizing the metal).
Maximum kinetic energy of the electron Ek is equal to the work done by electric forces when the electron passes through the so-called breaking voltage. Electric work is given by the product of the electron charge e and the voltage U
\[E_k=eU ,\]where e = 1.6·10−19 C is an elementary charge.
We will calculate the kinetic energies of the electrons and radiation frequencies, i.e. values from the Einstein’s equation from the measured data
radiation wavelength λ [nm] 433.9 404.7 365.0 312.5 253.5 radiation frequency f [Hz] 6.914·1014 7.413·1014 8.219·1014 9.600·1014 11.834·1014 stopping voltage U [V] 0.55 0.73 1.09 1.67 2.57 max. kinetic energy of the electron Ek [J] 0.880·10−19 1.168·10−19 1.744·10−19 2.672·10−19 4.112·10−19 We will plot the calculated values into a graph
Source data file (MS Excel)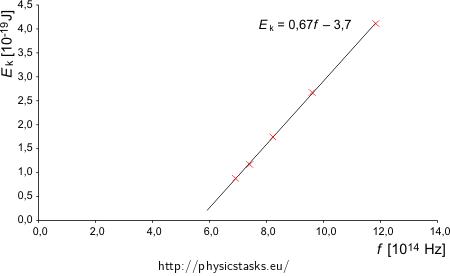
From the graph it is clear that the measured values indeed form a line, as the Einstein’s equation predicts (it is a linear function). We will use a linear fit and look at its equation (we can fit the data for example in MS Excel).
The frequency f is on the horizontal axis i.e. we will write f instead of x and kinetic energy Ek instead of y which is on the vertical axis. We obtain following equation
\[\frac{E_{\mathrm{k}}}{10^{-19}\,\mathrm{J}}=0.6616\frac{f}{10^{14}\,\mathrm{Hz}}-3.7039,\]we can simplify it by substitution of 1 Hz = 1 s−1
\[E_{\mathrm{k}}=\frac{0.6616{\cdot}10^{-19}\,\mathrm{J}}{10^{14}\,\mathrm{Hz}}f-3.7039{\cdot}10^{-19}\,\mathrm{J}\] \[E_{\mathrm{k}}=6.6{\cdot}10^{-34}\,\mathrm{Js}\,f-3{,}7{\cdot}10^{-19}\,\mathrm{J}.\]When we compare the obtained formula with general Einstein’s equation we can see that we have obtained
h = 6.6·10−34 JsWv = 3.7·10−19 J.Obtained Planck’s constant h satisfies the value from the tables.
Furthermore, in tables we can find that the output work Wv for lithium is 2.36 eV. If we use the conversion between eV and J where 1 eV = 1.6·10−19 J we get
Wv = 2.36 eV = 2.36·1,6·10−19 J = 3.8·10−19 J,Which also corresponds nicely to the measured value.
Answer
From the measured data we obtained the Planck’s constant h = 6.6·10−34 Js and output work for lithium Wv = 3.7·10−19 J. Both values correspond well to the table values.




