Zbiór rozwiązanych zadań i problemów fizycznych

Wyznaczenie stałej Plancka i pracy wyjścia z danych eksperymentalnych dla zjawiska fotoelektrycznego

Kod zadania: 1095

• Podpowiedź

  Do rozwiązania zadania niezbędna jest znajomość równania Einsteina dla zjawiska fotoelektrycznego, które określa maksymalną energię kinetyczną E_k uwalnianych elektronów:

  \[E_k=hf-W_v,\]

  gdzie iloczyn stałej Plancka h i częstotliwości promieniowania f określa energię pojedynczego padającego fotonu, a W_v to tzw. praca wyjścia (stała charakteryzująca dany metal).

  Równanie to mówi nam, że pomiędzy częstotliwością promieniowania a maksymalną energią kinetyczną wybijanych elektronów istnieje liniowa zależność. Najprościej będzie więc przeliczyć podane długości fali na częstotliwości, a z napięcia hamowania określić energię kinetyczną elektronów. Następnie wielkości te przedstawić graficznie, dopasować prostą, a z jej równania określić zadane stałe.

  Dopasowanie prostej – tzw. regresję liniową – można wykonać na wykresie, z użyciem kalkulatora, można też posłużyć się jednym z programów komputerowych, np. MS Excel.

• Analiza

  W zjawisku fotoelektrycznym zaobserwowano, że padające na powierzchnię metalu światło (czy też ogólniej: promieniowanie elektromagnetyczne) może w pewnych warunkach uwalniać z metalu elektrony, tworzące tzw. prąd fotoelektryczny. Zjawisko to wyjaśnił A. Einstein, podając odpowiednie równanie, określające maksymalną energię kinetyczną E_k uwalnianych elektronów.

  Maksymalną energię kinetyczną elektronów mierzymy przy pomocy napięcia hamowania, tj. poprzez pomiar napięcia, przy którym żaden uwolniony elektron nie zamyka już obwodu prądu (prąd przestaje płynąć). Praca, którą wykonują siły elektryczne, zatrzymując elektron, równa jest energii kinetycznej, którą posiadał on po uwolnieniu.

  W równaniu Einsteina występują praca wyjścia i stała Plancka; będziemy mogli określić te stałe, porównując podane zmierzone w zjawisku wielkości.

• Rozwiązanie

  Przypomnijmy równanie Einsteina dla zjawiska fotoelektrycznego, określające maksymalną energię kinetyczną E_k uwalnianych elektronów:

  \[E_k=hf-W_v,\]

  gdzie iloczyn stałej Plancka h i częstotliwości promieniowania f określa energię pojedynczego padającego fotonu, a W_v to tzw. praca wyjścia (stała charakteryzująca dany metal).

  Maksymalna energia kinetyczna elektronu E_k równa jest pracy, którą wykonają siły elektryczne, gdy elektron zatrzymany zostanie przez tzw. napięcie hamowania. Pracę w polu elektrycznym możemy określić jako iloczyn ładunku elektronu e i napięcia U, tj. zachodzi

  \[E_k=eU,\]

  gdzie e = 1,6·10⁻¹⁹ C to ładunek elementarny.

  Ze zmierzonych danych wyznaczymy energię kinetyczną elektronów i częstotliwość promieniowania, tj. wielkości, które występują w równaniu Einsteina:

  długość fali promieniowania λ [nm]	433,9	404,7	365,0	312,5	253,5
  częstotliwość promieniowania f [Hz]	6,914·1014	7,413·1014	8,219·1014	9,600·1014	11,834·1014
  napięcie hamowania U [V]	0,55	0,73	1,09	1,67	2,57
  maks. energia kinetyczna elektronu Ek [J]	0,880·10−19	1,168·10−19	1,744·10−19	2,672·10−19	4,112·10−19

  Obliczone wartości przedstawimy na wykresie:

  

  Plik źródłowy (MS Excel)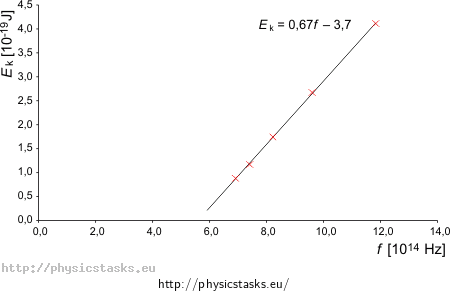

  Z wykresu widzimy, że zmierzone wielkości rzeczywiście leżą na prostej, jak przewiduje równanie Einsteina (funkcja liniowa). Spróbujmy określić równanie prostej (np. w programie MS Excel postulując trend liniowy).

  Na osi odciętych jest częstotliwość f, tj. zamiast x zapiszmy f, a zamiast y energię kinetyczną E_k na osi rzędnych. Pozostawmy takie rzędy jednostek, których używaliśmy przy sporządzaniu wykresu. Otrzymujemy równanie:

  \[\frac{E_{\mathrm{k}}}{10^{-19}\,\mathrm{J}}=0{,}6616\frac{f}{10^{14}\,\mathrm{Hz}}-3{,}7039\]

  Równanie to przekształcimy i podstawimy wyrażenie 1 Hz = 1 s⁻¹.

  \[E_{\mathrm{k}}=\frac{0{,}6616{\cdot}10^{-19}\,\mathrm{J}}{10^{14}\,\mathrm{Hz}}f-3{,}7039{\cdot}10^{-19}\,\mathrm{J}\] \[E_{\mathrm{k}}=6{,}6{\cdot}10^{-34}\,\mathrm{Js}\,f-3{,}7{\cdot}10^{-19}\,\mathrm{J}\]

  Porównując otrzymane równanie z równaniem Einsteina, otrzymujemy:

  h = 6,6·10⁻³⁴ Js

  W_v = 3,7·10⁻¹⁹ J

  Wyznaczona stała Plancka h zgadza się z wartością z tablic.

  Możemy też sprawdzić w tablicach, że praca wyjścia W_v dla litu wynosi 2,36 eV. Skorzystamy z przeliczenia jednostek energii 1 eV = 1,6·10⁻¹⁹ J, otrzymując

  W_v = 2,36 eV = 2,36·1,6·10⁻¹⁹ J = 3,8·10⁻¹⁹ J,

  co też zupełnie nieźle zgadza się z wyznaczoną wartością.

• Odpowiedź

  Ze zmierzonych danych wyznaczyliśmy stałą Plancka h = 6,6·10⁻³⁴ Js i pracę wyjścia dla litu W_v = 3,7·10⁻¹⁹ J. Obie wielkości zgadzają się z wartościami z tablic.