Výkon motoru pásového dopravníku
Úloha číslo: 1249
Uhlí padá ze zásobní násypky na vodorovný pásový dopravník, který jej transportuje ke kontrole a dalšímu zpracování.
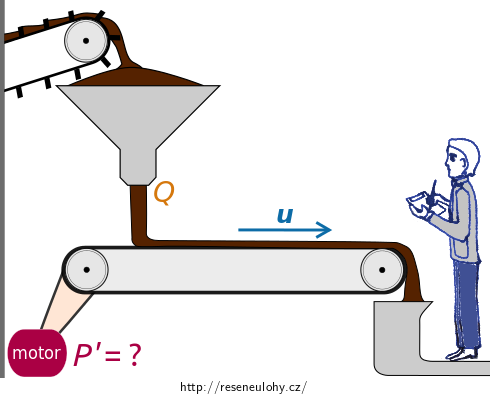
Určete výkon motoru pohánějícího dopravník, jestliže hmotnostní tok uhlí padajícího z násypky je \(375~\mathrm{kg\cdot s^{-1}}\) a pás s materiálem se pohybuje rychlostí \(3~\mathrm{m\cdot s^{-1}}\).
Předpokládejte, že \(5\,\mathrm{\%}\) celkového výkonu motoru připadá na překonávání tření (v ložiskách, řemenicích, pásu atd.).
Zápis
\(u = 3~\mathrm{m\cdot s^{-1}}\) rychlost dopravovaného materiálu na pásu \(Q = 375~\mathrm{kg\cdot s^{-1}}\) hmotnostní tok materiálu z násypky \(\frac{P'-P}{P'} = 5~\mathrm{\%}\) podíl celkového výkonu motoru \(P'\) připadající na ztráty třením
\(P'=\mathrm{?}\) Hledaný celkový výkon motoru Rozbor
Úlohu řešme z pohledu vnějšího pozorovatele, tedy kontrolora stojícího u pásu.
Na vodorovný dopravní pás z násypky spojitě dopadá materiál s konstantním hmotnostním tokem. Sledujme nyní malý hmotnostní element materiálu.
Bezprostředně po dopadu na pás se element hmotnosti dle prvního Newtonova zákona snaží setrvávat v pohybu. Ve vertikálním směru je mu setrvávání v pohybu zamezeno reakční silou pásu. Ve směru horizontálním má element před dopadem nulovou rychlost. Dopadem na pás začne na element působit třecí síla, která jej urychlí na rychlost pásu. Poté si sledovaný element svou rychlost drží, jeho hybnost se nemění a k udržení jeho pohybového stavu není třeba další síly, a tedy ani práce.
Uvažujme soustavu dopadajícího elementu a pásu a sledujme hybnost v horizontálním směru, tj. ve směru pásu. Při dopadu je hybnost v tomto směru nulová. Po určitém čase však element získá rychlost pásu, tedy i nenulovou hybnost. Hybnost soustavy vzroste. Původcem tohoto vzrůstu musí být dle první věty impulsové síla vnější.
Vnější síla je rovna časové změně hybnosti soustavy. Práce vnější síly závisí na její velikosti, směru a dráze, po které působí. Výkon příslušející mechanické práci potřebné na urychlení materiálu je pak časovou derivací této práce. Celkový vynaložený výkon motoru pak čítá i ztráty v podobě tření v ložiskách, prokluzování, smýkání atp.
Přepravuje-li pás daný hmotnostní tok materiálu, má motor příslušný hledaný výkon. V případě, že pás necháme běžet naprázdno, není konána žádná užitečná mechanická práce. Elektromotor však energii spotřebovává. Je to dáno tím, že se koná práce neužitečná v podobě tření v ložiskách, řemenicích, dochází k prokluzování, smýkání atp. Tyto ztráty dle zadání činí \(5\,\mathrm{\%} \) celkového výkonu motoru.
Je důležité si uvědomit následující. Poté, co přerušíme tok materiálu na pás a všechen dopadnutý materiál je urychlen na rychlost pásu, se již žádná (užitečná) práce nekoná! Materiál již má svou konstantní rychlost i hybnost a k setrvání tohoto pohybového stavu není třeba žádné vnější síly, tedy ani práce a výkonu. Celkový výkon motoru je, pomineme-li zvýšení tření díky zatížení pásu, stejný jako v případě, že pás běží naprázdno.
Průpravná rukojeť
Hybnost tělesa
Hybnost tělesa představuje míru setrvačnosti tělesa. Má-li hmotnost \(m\) a rychlost \(\vec v\), je jeho hybnost \(\vec p\) dána vztahem \[\vec p = m \vec v.\]Zákon zachování hybnosti
Celková hybnost izolované soustavy je konstantní. Pozor, hybnost je vektor, nutno ji sčítat vektorově. Platí tedy \[\vec{p}_\mathrm{soustavy} = \sum_{i=1}^{n} \vec p_i = \sum_{i=1}^{n} m_i\vec v_i = \overset{\longrightarrow}{konst.}\] Jedná se o vektorovou rovnici, zákon zachování musí platit i ve složkách vektorů. Budeme-li se například pohybovat v soustavě \(Oxy\), platí: \[ \sum_{i=1}^{n} p_x = \mathrm{konst}_x, \qquad \sum_{i=1}^{n} p_y = \mathrm{konst}_y.\]První věta impulsová
Mění-li se celková hybnost soustavy, působí na ni nějaké vnější síly. První věta impulsová říká, že celková časová změna hybnosti soustavy je rovna výslednici vnějších sil na ni působících. Tedy \[\vec{F_\mathrm{ex}} = \frac{\mathrm{d}\vec{p}}{\mathrm{d}t} = \lim_{\Delta t\to 0} \frac{\Delta \vec{p}}{\Delta t} .\]Práce síly
Práce síly \(\vec{F}(\vec{r})\) po křivce \(\Sigma\) je dána obecně vztahem \[W = \int_\Sigma \vec{F}\left(\vec{r}\right)\cdot \mathrm{d}\vec{r}. \] Dojde-li působením konstantní síly \(\vec F\) k posunu tělesa po vektoru posunutí \(\vec a\), vztah se nám zjednoduší na \[W = \vec{F}\cdot \vec{a} = Fa\cos \alpha.\] Ve speciálním případě, kdy konstantní síla koná práci ve směru pohybu po dráze \(a\) \((\cos 0^\mathrm{\circ} = 1)\), lze jednoduše psát \[W = Fa.\]Výkon
Abychom mohli posuzovat „pracovitost“ strojů, hodí se nám znát, kolik práce vykonají za jednotku času. Za tím účelem zavádíme výkon jako práci dělenou časem, který je třeba k jejímu vykonání. Během takového času může stroj pracovat nerovnoměrně, proto vztah \[\bar{P} = \frac{\Delta W}{\Delta t}\] představuje střední výkon za čas \(\Delta t\). Zajímá-li nás výkon okamžitý, budeme „kontrolní“ čas, po který kontrolujeme vykonanou práci, limitně zmenšovat, tj. \[P = \lim_{\Delta t \to 0} \frac{\Delta W}{\Delta t} = \frac{\mathrm{d}W}{\mathrm{d}t}.\] Okamžitý výkon je tedy derivací vykonané práce podle času, tj. je roven okamžitému časovému vzrůstu vykonané práce.Nápověda 1 – změna hybnosti elementu, urychlovací síla
Zaveďme soustavu souřadnic dle obrázku. Budeme sledovat pouze jeden malý element hmotnosti \(\Delta m\).
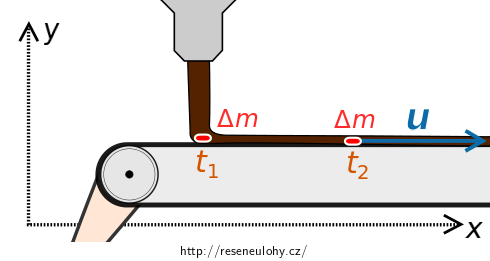
Jak se změní hybnost tohoto elementu ve směru osy \(x\) od dopadu na pás po urychlení na rychlost pásu?
Vyjádřete vektor působící vnější síly, která zapřičiňuje tuto změnu hybnosti, pomocí hmotnostního toku \(Q\) a rychlosti pásu s materiálem \(\vec u\) .
Nápověda 2 – práce externí urychlující síly
V předchozí části jsme vyjádřili sílu potřebnou k urychlení materiálu na rychlost pásu. Vyjádřete nyní celkovou práci této síly na dráze dané vektorem posunutí pásu \(\vec{s}\). Při výpočtu vycházejte z obecného vztahu pro práci \(W = \int_\Sigma \vec F \cdot \mathrm{d}\vec r\).Nápověda 3 – výkon síly urychlující materiál
Výkon motoru je určen množstvím práce vykonané za jednotku času. Okamžitý výkon je derivací konané práce podle času.
Nalezněte výkon jako časovou derivaci práce, kterou vyjadřuje vztah (5).
Nápověda 4 – celkový výkon motoru
Vypočítejte celkový výkon motoru \(P'\), ztrácí-li se \(5\,\mathrm{\%}\) celkového výkonu třením v ložiskách, řemenicích atp.
To znamená, že \(95\,\mathrm{\%}\) celkového výkonu připadá na užitečné transportování hmoty materiálu, tedy na právě vypočítáný výkon \(P\).
Poznámka
Vypočítaný výkon \(P' = 3{,}7~\mathrm{kW}\) odpovídá z pohledu motoru stále „užitečné“ práci, neobsahuje ztráty energie v motoru. Neztrátovost motoru charakterizuje jeho účinnost \[\eta = \frac{P'}{P_0},\] kde \(P'\) je výstupní výkon motoru (odpovídá momentu síly potřebnému k udržení funkce aktivního pásového dopravníku) a \(P_0\) příkon motoru odpovídající spotřebě energie ze sítě. Účinnost běžných elektromotorů bývá kolem \(90\,\mathrm{\%}\).Vinutí třífázových motorů, které se pro bezproblémovost chodu a údržby v průmyslových aplikacích hojně využívají, tvoří cívky, které kolem sebe vytvářejí točivé magnetické pole roztáčející rotor. Cívky nejsou ničím jiným než vodiči a průchodem proudu se zahřívají. Ztráty motoru tedy odpovídají Jouleovu teplu generovanému na jeho vinutí.
Se vzrůstem teploty vodiče roste jeho odpor. Z těchto důvodů je motor zpravidla chlazen. Na ose rotoru je umístěna vrtule, která motorem, respektive žebrováním jeho kovového šasi, prohání vzduch (viz fotografie).
Celkové řešení
Zavedeme soustavu souřadnic dle obrázku. Budeme sledovat pouze jeden malý element hmotnosti \(\Delta m\).
Při dopadu sledovaného elementu hmotnosti \(\Delta m\) materiálu na pás je jeho rychlost, a tedy i hybnost ve směru osy \(x\) nulová. Po styku s pásem je element urychlen na rychlost pásu \(\vec{u}\). Změnu hybnosti elementu \(\Delta m\) ve směru osy \(x\) od dopadu po urychlení na rychlost pásu \(\vec{u}\) můžeme matematicky vyjádřit \[\Delta \vec{p_{x}} = \vec{p_{{x}_2}} - \vec{p_{{x}_1}} = \Delta m \,\vec{u} -\Delta m \cdot \vec{0} = \Delta m\,\vec{u}.\tag{1}\] Časová změna hybnosti tělesa je dle první věty impulsové rovna působící vnější síle. Vektor síly zodpovědný za urychlení elementu je tedy s použitím (1) \[\vec{F_\mathrm{ex}} = \lim_{\Delta t \to 0} \frac{\Delta p_{x}}{\Delta t} = \lim_{\Delta t \to 0} \frac{\Delta m\,\vec u}{\Delta t}. \tag{2}\] Hmotnostní tok materiálu z násypky je \(Q\). Tato veličina představuje časovou změnu hmotnosti, matematicky zapsáno \[Q = \frac{\mathrm{d}m}{\mathrm{d}t}=\lim_{\Delta t \to 0}\frac{\Delta m}{\Delta t}.\tag{3}\] Protože je vektor rychlosti \(\vec u\) v limitě rovnice (2) konstantní, lze jej vytknout před limitu. Zbylá limita je pak přímo vyjádřením hmotnostního toku \(Q\) dle rovnice (3): \[\vec{F_\mathrm{ex}} = \lim_{\Delta t \to 0} \frac{\Delta m\,\vec u}{\Delta t} = \vec u \lim_{\Delta t \to 0} \frac{\Delta m}{\Delta t} = \vec u\, Q. \tag{4}\]
Vyjádřili jsme sílu potřebnou k urychlení materiálu na rychlost pásu. Nyní vyjádříme celkovou práci této síly na dráze dané vektorem posunutí pásu \(\vec{s}\). Při výpočtu budeme vycházet z obecného vztahu pro práci \(W = \int_\Sigma \vec F \cdot \mathrm{d}\vec r\).
Do obecného vyjádření práce \(W\) externí síly \(\vec{F_\mathrm{ex}}\) dosadíme z rovnice (4): \[W = \int \vec{F_\mathrm{ex}}\cdot \mathrm{d}\vec{r} = \int Q\,\vec{u}\cdot \mathrm{d}\vec{r}.\] Hmotnostní tok \(Q\) a vektor rychlosti \(\vec{u}\) jsou konstantní, lze je tedy vytknout před integrál: \[\int Q\,\vec{u}\cdot \mathrm{d}\vec{r}= Q\,\vec{u} \cdot \int \mathrm{d}\vec{r}. \] Integrací elementárních posunutí \(\mathrm{d}\vec{r}\) dostaneme celkové posunutí \(\vec{s}\): \[Q\,\vec{u} \cdot \int \mathrm{d}\vec{r} = Q\,\vec{u} \cdot \vec{s}. \] Díky rovnoběžnosti vektorů přejde jejich skalární součin v součin jejich velikostí: \[Q\,\vec{u} \cdot \vec{s} = Qus. \]
Práce síly urychlující materiál je tedy \[W = Qus,\tag{5}\]kde \(Q\) je hmotnostní tok materiálu, \(u\) velikost rychlosti pásu a \(s\) posunutí pásu.
Poznámka: Vztah byl odvozen při existenci hmotnostního toku \(Q\). Pokud by materiál přestal padat, byla by tato práce po urychlení poslední dopadnuté hmoty nulová!Výkon síly, která materiál urychluje, je dán časovou derivací její vykonané práce. Práci síly vyjadřuje vztah (5):
\[P = \frac{\mathrm{d}W}{\mathrm{d}t} = \frac{\mathrm{d}}{\mathrm{d}t}\left(Q u s \right).\]Hmotnostní tok \(Q\) a vektor rychlosti posunu pásu \(\vec u\) jsou s časem neměnné, lze je tedy vytknout před derivaci:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(Q u s \right) = Qu\frac{\mathrm{d}s}{\mathrm{d}t}.\]Derivace velikosti vektoru posunutí pásu podle času není nic jiného, než velikost rychlosti jeho pohybu, tj. \(u\):
\[Qu\frac{\mathrm{d}s}{\mathrm{d}t} = Qu^2.\]
Výkon potřebný k urychlování hmotnostního toku \(Q\) materiálu na rychlost pásu \(u\) je roven \[P = Q u^2.\tag{6}\]Připadá-li \(5\,\mathrm{\%}\) celkového výkonu motoru na překonávání tření, připadá \(95\,\mathrm{\%}\) na vypočítaný výkon \(P\) potřebný k transportu materiálu. Označíme-li celkový výkon motoru \(P'\), lze psát
\[\frac{P}{P'} = 0{,}95 = 95\,\mathrm{\%}.\]Odtud a s použitím rovnice (6) pro hledaný výkon pišme
\[P' = \frac{P}{0{,}95} = \frac{Qu^2}{0{,}95} = \frac{375{\cdot} 3^2}{0{,}95}~\mathrm{kW} \doteq 3{,}7~\mathrm{kW}.\]Odpověď
Výkon motoru pohánějící pásový dopravník závisí na hmotnostím toku v první mocnině a na rychlosti pohybu pásu v mocnině druhé. Chceme-li zvýšit rychlost přepravy materiálu nebo hmotnostní tok, musíme použít motor s vyšším výkonem.
Pro daný hmotnostní tok a rychlost pásu je výkon motoru přibližně \(3{,}7~\mathrm{kW}\).




