Jojo
Úloha číslo: 2306
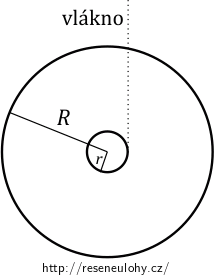
Jojo je vyrobeno ze dvou plechových kotoučů o hustotě \(\rho\), tloušťce \(d\) a poloměru \(R\) spojených krátkou osičkou o poloměru \(r\).
Určete moment setrvačnosti joja vzhledem k rotační ose symetrie. Moment setrvačnosti i hmotnost osičky zanedbejte.
Vlákno navinuté na osičce má délku \(L\) a zanedbatelnou tloušťku. S jakým zrychlením se odvaluje jojo dolů podél vlákna?
Jak velkou tahovou silou působí vlákno na jojo?
Rozbor
Zanedbáváme-li hmotnost a moment setrvačnosti osičky, můžeme se na jojo dívat jako na dva disky stejné hmotnosti. Ze známého vztahu pro moment setrvačnosti disku lze odvodit moment setrvačnosti joja. Hmotnost jednoho disku spočítáme z jeho hustoty a objemu.
Zrychlení, se kterým se jojo odvaluje dolů podél vlákna, souvisí se silami působícími na jojo, tedy s tíhovou silou a tahovou silou vlákna. (Uvažujeme, že je jojo volně puštěné, tedy že na něj hráč nepůsobí silou.) Pohyb joja je složen ze zrychleného posuvného pohybu a pohybu rotačního okolo osy symetrie. Abychom zjistili zrychlení posuvného pohybu (zrychlení těžiště joja), napíšeme pohybovou rovnici pro působící síly a pro momenty působících sil vzhledem k těžišti.
Situaci lze také zkoumat z pohledu zákona zachování mechanické energie. V tom případě zvolíme nulovou hladinu potenciální energie a vybereme dvě situace, ve kterých srovnáme celkovou mechanickou energii joja.
Nápověda a)
Jelikož zanedbáváme hmotnost a moment setrvačnosti osičky, můžeme si jojo představit jako dva homogenní tlusté disky. Zkuste si vzpomenout, jak se počítá moment setrvačnosti obyčejného disku, a upravte jej pro náš případ. Pozor na správné hmotnosti.
Řešení a)
Moment setrvačnosti jednoho homogenního disku o hmotnosti \(m_1\) a poloměru \(R\) je
\[J_\mathrm{disk}=\frac{1}{2} m_1R^2.\]
Jojo se skládá ze dvou takových disků, moment setrvačnosti \(J_\mathrm{disk}\) tedy budeme uvažovat dvakrát. Hmotnost jednoho disku můžeme vyjádřit pomocí součinu jeho objemu a hustoty, která je stejná jako hustota joja \(\rho\). Dostáváme
\[J=2\,J_\mathrm{disk}= m_1R^2=\rho\,V_\mathrm{disk}R^2.\]
Disk považujeme za válec, pro jehož objem platí:
\[V_\mathrm{disk}=\pi R^2 d,\]
kde \(d\) je tloušťka (nebo také výška) disku joja.
Pro moment setrvačnosti joja pak dostáváme:
\[J=\rho\,\pi R^2 dR^2= \pi \rho R^4d. \]
Chceme-li vyjádřit moment setrvačnosti pomocí hmotnosti joja \(m\), dosadíme do získaného vztahu za hustotu \(\rho\), která je rovna podílu hmotnosti joja \(m\) a jeho celkového objemu \(V\) (objemu dvou kotoučů):
\[J=\pi R^4 d \frac{m}{2\pi R^2 d}.\]
Výraz na pravé straně upravíme a získáme výsledný tvar pro moment setrvačnosti joja:
\[J= \frac{1}{2}mR^2.\]
Nápověda b)
Zrychlení, se kterým se jojo odvaluje dolů podél vlákna, můžeme určit z působících sil. Nakreslete obrázek s vyznačením všech sil působících na jojo. (Uvažujeme, že je jojo volně puštěné, tedy že na něj hráč nepůsobí silou.) Sestavte pohybovou rovnici pro posuvný i rotační pohyb joja.
Druhou možností je využít zákon zachování mechanické energie. V tom případě nejprve zvolte nulovou hladinu potenciální energie, dále vyberte dvě situace a srovnejte celkovou mechanickou energii joja v těchto situacích.
Řešení b) – Pohybové rovnice
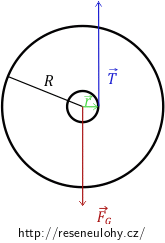
Chceme-li určit zrychlení pomocí rozboru působících sil a sestavení pohybových rovnic, nakreslíme si nejprve obrázek a vyznačíme působící síly. Těmi jsou tíhová síla \(\vec {F_\mathrm{G}}\), která působí v těžišti, a tahová síla vlákna \(\vec T\), která působí směrem vzhůru v místě, kde se vlákno odvíjí od osičky joja.
Jojo se pohybuje zrychleně směrem dolů, to znamená, že výslednice sil je nenulová. Platí
\[\vec {F_\mathrm{G}}+\vec {T} = m\vec a,\]
kde \(a\) je velikost hledaného zrychlení. Pohybovou rovnici můžeme přepsat skalárně
\[F_\mathrm{G}-T=ma.\]
Dosadíme vyjádření tíhové síly:
\[mg-T=ma.\tag{1}\]
Tahovou sílu vlákna zatím neumíme vyjádřit, zůstává nám v rovnici jako neznámá. Potřebujeme ještě jednu rovnici, kterou nám dodá druhá věta impulsová. Momenty sil budeme určovat vzhledem k těžišti joja, neboť je to zároveň působiště tíhové síly \(\vec {F_\mathrm{G}}\). Jelikož velikost polohového vektoru tíhové síly \(F_\mathrm{G}\) je nulová, je i moment této síly nulový. Zbývá tedy moment tahové síly vlákna. Platí tedy
\[\vec r × \vec T = J \vec\epsilon,\]kde \(\vec r\) je polohový vektor spojující těžiště joja a působiště tahové síly, \(J\) je moment setrvačnosti joja a \(\vec \epsilon\) je jeho úhlové zrychlení.
Jelikož síla \(\vec T\) má směr tečny k osičce, je úhel mezi vektorem \(\vec r\) a silou \(\vec T\) pravý a pro velikost vektorového součinu platí
\[|\vec r × \vec T|=rT sin{\alpha}=rT.\]
Získáme následující skalární vyjádření druhé impulsové věty:
\[Tr=J\epsilon.\]
Úhlové zrychlení můžeme vyjádřit jako
\[\epsilon = \frac{a}{r}.\]
Pak:
\[Tr=J\frac{a}{r}.\tag{2}\]
Dosadíme-li za tahovou sílu \(T\) z rovnice (2) do rovnice (1) , získáme
\[mg-ma=J\frac{a}{r^2}.\]
Vyjádříme zrychlení \(a\) a dosadíme za moment setrvačnosti joja \(J\):
\[a\left (m+\frac{J}{r^2} \right)=mg,\]
\[a=\frac {mg}{\left (m+\frac{J}{r^2} \right)},\]
\[a=\frac {g}{\left (1+\frac{J}{mr^2} \right)}=\frac {g}{\left (1+\frac{mR^2}{2mr^2} \right)}=\frac {g}{\left (1+\frac{R^2}{2r^2} \right)}.\]
Úpravou získáme
\[a=\frac {2gr^2}{2r^2+R^2}.\]
Řešení b) – ZZME
Vyjdeme ze zákona zachování mechanické energie. Vybereme dvě situace, v nichž srovnáme mechanické energie: První z nich zvolíme pro jojo v klidu, těsně před tím, než jej hráč volně pustí, druhou situaci zvolíme po odmotání délky \(l\) vlákna (tehdy má jojo největší kinetickou energii). Nulovou hladinu potenciální energie zvolíme ve druhé situaci v úrovni těžiště (kdy se těžiště joja bude nacházet nejníž nad zemí). Pro energie pak platí
\[E_\mathrm{p} = E_\mathrm{t}+E_\mathrm{r},\tag{3}\]
kde \(E_\mathrm{p}\) je potenciální energie, \(E_\mathrm{t}\) je kinetická energie posuvného (translačního) pohybu a \(E_\mathrm{r}\) je kinetická energie rotačního pohybu.
Pro jednotlivé typy energií platí:
\[E_\mathrm{p}=mgl,\]
\[E_\mathrm{t}=\frac{1}{2}mv^2,\]
\[E_\mathrm{r}=\frac{1}{2}J\omega^2,\]
kde rychlost \(v\) představuje rychlost posuvného pohybu a \(\omega\) je rychlost rotačního pohybu joja.
Úhlovou rychlost můžeme vyjádřit jako podíl rychlosti \(v\) a poloměru otáčení \(r\).
Výše získané poznatky dosadíme do rovnice (3):
\[mgl=\frac{1}{2}mv^2+\frac{1}{2}J\frac{v^2}{r^2}.\tag{4}\]
Nyní potřebujeme vyjádřit rychlost v rovnici pomocí zrychlení. Víme, že těžiště joja se pohybuje rovnoměrně zrychleným pohybem a (v námi pozorovaných situacích) urazí dráhu \(l\). Pro dráhu a rychlost rovnoměrně zrychleného pohybu platí:
\[v=at,\]
\[l=\frac{1}{2}at^2.\]
Odtud pro kvadrát rychlosti \(v^2\) dostáváme
\[v^2=2la.\]
Dosazením do rovnice (4) za \(v^2\) získáme rovnici o jedné neznámé \(a\). Rovnici upravíme a zrychlení \(a\) vyjádříme:
\[mgl=\frac{1}{2}m2la+\frac{1}{2}J\frac{2la}{r^2},\]
\[mg=ma+a\frac{J}{r^2},\]
\[mg=a\left(m+\frac{J}{r^2}\right),\]
\[a=\frac{g}{1+\frac{J}{mr^2}}.\]
Dosadíme-li za moment setrvačnosti \(J\) z první části úlohy, můžeme zrychlení vyjádřit též následujícím způsobem:
\[a=\frac{g}{1+\frac{R^2}{2r^2}}=\frac {2gr^2}{2r^2+R^2}.\]
Nápověda c)
Podívejte se na pohybovou rovnici, kterou jsme sestavili v řešení b). S její pomocí již tahovou sílu vlákna \(T\) snadno určíte.
Řešení c)
V řešení b) jsme sestavili pohybovou rovnici (1) pro působící síly. V té samé části úlohy jsme vyjádřili zrychlení \(a\), se kterým se jojo odvaluje dolů podél vlákna. Z pohybové rovnice (1) vyjádříme hledanou sílu \(T\) a dosadíme za zrychlení \(a\):
\[mg-ma=T,\]
\[T=m\left(g-a\right)=m\left(g-\frac{2gr^2}{2r^2+R^2}\right)=\left(\frac{mgR^2}{2r^2+R^2}\right).\]
Tahovou sílu vlákna můžeme vyjádřit v závislosti na momentu setrvačnosti \(J\):
\[T=\frac{mg}{1+\frac{mr^2}{J}}.\]
Odpověď a)
Moment setrvačnosti joja je
\[ J=\pi \rho R^4d.\]Vztah můžeme vyjádřit v závislosti na hmotnosti joja \(m\) a jeho poloměru \(R\):
\[J= \frac{1}{2}mR^2.\]
Odpověď b)
Podél vlákna se jojo odvaluje se zrychlením
\[a=\frac {2gr^2}{2r^2+R^2}.\]
Odpověď c)
Vlákno působí na jojo tahovou silou o velikosti
\[T=\left(\frac{mgR^2}{2r^2+R^2}\right)=\frac{mg}{1+\frac{mr^2}{J}}.\]



