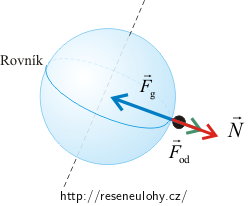
Odstředivá síla na rovníku
Úloha číslo: 200
Může člověk stojící na rovníku „uletět“ vlivem odstředivé síly?
Poloměr Země na rovníku je 6378 km, úhlová rychlost rotace Země je 7,29·10−5 s−1. Hmotnost člověka předpokládejte 80 kg.
Zápis
R = 6378 km poloměr Země ω = 7,29·10−5 s−1 úhlová rychlost rotace Země m = 80 kg hmotnost člověka Fod = ? odstředivá síla Z tabulek:
Mz = 5,97·1024 kg hmotnost Země κ = 6,67·10−11 N m2 kg−2 gravitační konstanta Nápověda 1
Úlohu řešte z hlediska soustavy rotující spolu se Zemí. Jaké síly působí na člověka? Co platí pro jejich výslednici?
Nápověda 2 – velikosti sil
Rozmyslete si, co by muselo platit pro velikosti působích sil, aby člověk odletěl.
Spočítejte velikost gravitační a odstředivé síly působící na člověka na rovníku.
Celkové řešení
Úlohu budeme počítat z hlediska soustavy rotující spolu se Zemí.
Na člověka stojícího na Zemi působí z hlediska neinerciální vztažné soustavy spojené s rotující Zemí gravitační síla, kterou ho přitahuje Země. Dále do něj tlačí země, na které stojí, a působí na něj odstředivá síla.
Vzhledem k rotující Zemi je člověk v klidu, takže výslednice těchto sil je nulová:
\[\vec{F}_\mathrm{g}\,+\,\vec{N}\,+\,\vec{F}_\mathrm{od}\,=\,\vec{o}.\]Pro velikost sil platí:
\[F_\mathrm{g} - N - F_\mathrm{od} = 0,\]a tedy:
\[F_\mathrm{g} = N + F_\mathrm{od}.\]Kdyby měl člověk „odletět“, znamenalo by to, že ztratí kontakt se Zemí a ta do něj přestane tlačit. Velikost gravitační síly by v tomto okamžiku byla rovna velikosti odstředivé síly. Spočítejme tedy velikosti obou sil.
Velikost odstředivé síly:
\[F_\mathrm{od} = m\frac{v^{2}}{R} = m\omega^{2}R = 80\,\cdot\, \left(7{,}29{\cdot}10^{-5}\right)^{2}\,\cdot \, 6378{\cdot}10^{3} \,\mathrm{N}\dot{=} 2{,}7\,\mathrm{N}.\]Velikost gravitační síly:
\[F_\mathrm{g} = \kappa \frac{mM_\mathrm{z}}{R^{2}} = 6{,}67{\cdot}10^{-11}\,\cdot\,\frac{80\, \cdot \, 5{,}97{\cdot}10^{24}}{\left(6378{\cdot}10^{3}\right)^{2}}\,\mathrm{N} \dot{=} 783{,}1\,\mathrm{N}.\]Porovnáme-li velikosti těchto sil, vyjde nám, že člověk vlivem odstředivé síly uletět nemůže.
Odpověď
Člověk vlivem odstředivé síly uletět nemůže. Jeho tíha (síla, kterou tlačí na zem) se vlivem odstředivé síly sníží jen asi o 0,3 %.Poznámka
Zkusme spočítat, jaká by musela být úhlová rychlost otáčení Země, aby člověk vlivem odstředivé síly „uletěl“. Aby se to stalo, musejí být gravitační a odstředivá síla stejně velké:
\[F_\mathrm{od} = F_\mathrm{g},\] \[m\omega^{2}R = \kappa\frac{mM_\mathrm{Z}}{R^{2}}.\]Nyní vyjádříme omega a číselně dosadíme:
\[\omega = \sqrt{\kappa\frac{M_\mathrm{Z}}{R^{3}}} = \sqrt{6{,}67{\cdot}10^{-11}\,\cdot\,\frac{5{,}97{\cdot}10^{24}}{\left( 6378{\cdot}10^{3}\right)^{3}}}\, \mathrm{s^{-1}}\dot{=} 1{,}24{\cdot}10^{-3}\,\mathrm{s^{-1}}.\]
Obvodová rychlost na rovníku je: \[v = \omega R = 1{,}24{\cdot}10^{-3}\,\cdot\, 6378{\cdot}10^{3}\,\mathrm{m \cdot s^{-1}}\dot{=}\,7909\,\mathrm{m \cdot s^{-1}}.\]Spočítejme ještě délku jednoho dne (tj. periodu otáčení):
\[T = \frac{2\pi}{\omega} = \frac{2\pi}{1{,}24{\cdot}10^{-3}}\,\mathrm{s}\, \dot{=}\, 5067\,\mathrm{s}\, \dot{=}\, 1{,}4\,\mathrm{h}. \]Tíhová a gravitační síla
1) Rozdíl mezi tíhovou a gravitační silou:
Tíhová síla se říká síle, která je výslednicí gravitační a odstředivé síly – míří tedy nepatrně jiným směrem než do středu Země a má nepatrně jinou velikost. Protože ale rozdíl velikostí a směrů tíhové a gravitační síly je velmi malý, často se zaměňují (např. v tomto příkladě činí odstředivá síla jen asi 0,3 % gravitační síly).
2) Jak jsme řekli, je tíhová síla výslednicí gravitační a odstředivé síly. Odstředivá síla závisí na poloměru rotace, který je jiný na rovníku a u nás na 50° s. š. (viz obrázek), takže je její velikost v každé zeměpisné šířce trochu jiná.
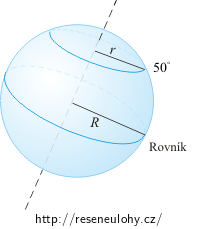
(Viz také řešení úlohy Pružinové váhy na pólu a na rovníku.)
Z tohoto důvodu není velikost tíhové síly v každém místě zemského povrchu stejná a není tedy všude stejné ani tíhové zrychlení –. Proto bylo jako konstanta přijato tzv. normální tíhové zrychlení: gn = 9,80665 m·s−2 (přesně) – odpovídá hodnotě tíhového zrychlení na 45° s. š. na úrovni mořské hladiny. Bylo přijato na 2. generální konferenci pro míry a váhy v roce 1901.Odkaz na podobnou úlohu