Valící se skruž
Úloha číslo: 2288
Betonová válcová skruž o hmotnosti \(M\) se valí bez smýkání dolů po svahu, který svírá s vodorovnou rovinou úhel \(\alpha\).
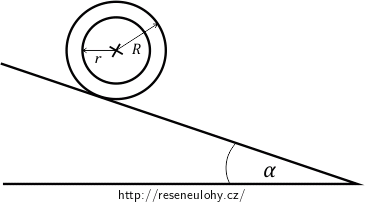
Rozbor
Válcovou skruž si můžeme představit jako dutý válec s tlustou stěnou. Předpokládáme, že skruž je homogenní (její hmota je rozmístěna rovnoměrně). Moment setrvačnosti můžeme určit buď z definice pomocí integrálu \(\int_V \rho r^2\mathrm{d}V\), nebo vyjít ze znalosti momentu setrvačnosti válce.
Zrychlení hmotného středu lze hledat pomocí zákona zachování mechanické energie. Platí, že celková mechanická energie skruže na vrcholu svahu je stejná jako její celková mechanická energie poté, co hmotný střed skruže urazí dráhu \(s\). Druhou možností, jak určit zrychlení hmotného středu, je udělat rozbor působících sil a jejich momentů a následně sestavit pohybové rovnice. Skruž se z vrcholu svahu, kde je v klidu, valí rovnoměrně zrychleným pohybem. Hmotný střed se pohybuje po přímce a urazí dráhu \(s\). Skruž nicméně koná pohyb jak posuvný, tak rotační. Výslednice sil i momentů sil působících na skruž je nenulová.
Nápověda a)
Vyjděte z obecného vztahu pro moment setrvačnosti a rozmyslete si, zda je možné si představit skruž rozsekanou na dílčí vrstvy, které budou vhodné pro počítání integrálu. Šikovné je volit vrstvu tak, aby byly všechny její části stejně vzdálené od osy otáčení. Nakreslete obrázek, vyznačte jednu takovou vrstvu a napište vyjádření momentu setrvačnosti této vrstvy.
Řešení a)
Moment setrvačnosti je definován integrálem
\[J = \int_{V} \rho r^2 \mathrm{d}V,\]
kde \(\rho\) je hustota tuhého tělesa a \(V\) jeho objem.
Skruž si představíme rozsekanou na jednotlivé slupky (viz obr. níže).
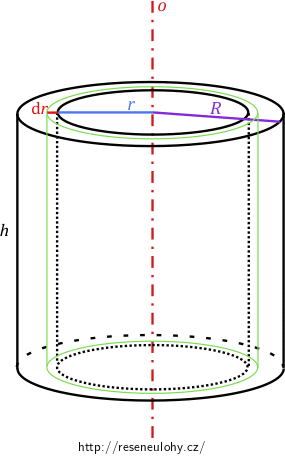
Pro moment setrvačnosti jedné takové slupky (na obrázku označené zelenou barvou) platí
\[\mathrm{d}J = r^2 \mathrm{d}m,\]
kde \(\mathrm{d}m\) je hmotnost slupky. Tu můžeme určit pomocí jejího objemu \(\mathrm{d}V\) a hustoty skruže \(\rho\):
\[\mathrm{d}m = \rho \mathrm{d}V = \rho 2h\pi r \mathrm{d}r.\]
Pro jednu slupku o poloměru \(r\) je tedy moment setrvačnosti roven
\[\mathrm{d}J = \rho 2h\pi r^3 \mathrm{d}r.\]
Abychom určili celkový moment setrvačnosti, stačí sečíst dílčí momenty setrvačnosti přes všechny slupky. Sčítat budeme od poloměru \(r\) do poloměru \(R\):
\[J = \int_{r}^{R}2\rho h \pi r^3 \mathrm{d}r = 2\rho h \pi\left [ \frac{r^4}{4}\right ]_{r}^{R} = \frac{\rho h \pi}{2}\left(R^4-r^4\right ). \]
Vyjádříme ještě hustotu \(\rho\) celé skruže pomocí celkové hmotnosti \(M\) a celkového objemu \(V\). Celkový objem vyjádříme jako rozdíl objemů dvou válců o poloměrech podstav \(R\) a \(r\):
\[\rho =\frac{M}{V}= \frac{M}{\pi R^2 h-\pi r^2 h}=\frac{M}{\pi h \left (R^2 -r^2\right )}.\]
Takto určenou hustotu dosadíme do integrálu, výraz upravíme a dostaneme konečný vztah pro moment setrvačnosti skruže. Využíváme úpravy vztahu podle matematického vzorce \(A^2-B^2=\left(A-B\right)\left(A+B\right)\):
\[J = \frac{M}{\pi h \left (R^2 -r^2\right )} \frac{h \pi}{2}\left(R^4-r^4\right )=\frac{M}{ 2} \frac{\left(R^2-r^2\right) \left(R^2+r^2\right)}{\left (R^2 -r^2\right )} = \frac{1}{2} M \left(R^2+r^2\right).\]
Poznámka
Moment setrvačnosti skruže lze také určit tak, že vyjdeme ze znalosti vztahu pro moment setrvačnosti válce
\[J=\frac{1}{2}MR^2\]
a od momentu setrvačnosti „plné“ skruže (válce s poloměrem \(R\)) odečteme moment setrvačnosti „díry“ (válce s poloměrem \(r\)):
\[J_\mathrm{skruže} = J_\mathrm{plné \ skruže} - J_\mathrm{díry},\] \[J_\mathrm{skruže} = \frac{1}{2}M_\mathrm{plné \ skruže}R^2 - \frac{1}{2}M_\mathrm{díry}r^2,\] \[J_\mathrm{skruže} = \frac{1}{2}\rho\pi R^2hR^2 - \frac{1}{2}\rho\pi r^2hr^2 = \frac{1}{2}\rho\pi h (R^4-r^4),\] \[J_\mathrm{skruže} = \frac{1}{2}\frac{M}{\pi h (R^2 - r^2)} \pi h(R^4-r^4),\] \[J_\mathrm{skruže} = \frac{1}{2}M (R^2+r^2).\]Nápověda b)
Zrychlení hmotného středu skruže lze určit dvěma způsoby: buď vyjdeme ze zákona zachování mechanické energie (ZZME), nebo si pomůžeme rozborem působících sil a vyřešíme pohybové rovnice. Rozmyslete si, ve kterých dvou situacích budete mechanické energie srovnávat, zvolte nulovou hladinu potenciální energie a příslušné energie zapište. V případě druhé metody načrtněte obrázek situace a vyznačte působící síly. Pokud vám nějaký údaj (vzdálenost, úhel…) chybí, můžete jej obecně zavést.
Řešení b) – ZZME
K řešení využijeme zákona zachování mechanické energie. Uvažujme dvě situace:
První, kdy se skruž nachází na vrcholu svahu (resp. hmotný střed je v nejvyšším bodě). Skruž stojí, neotáčí se, pouze potenciální energie \(E_\mathrm{p}\) má nenulovou hodnotu.
Druhou situaci zvolíme poté, co hmotný střed skruže urazí dráhu \(s\). V tento okamžik se skruž pohybuje nenulovou rychlostí, má tedy nenulovou kinetickou energii posuvného (translačního) pohybu \(E_\mathrm{t}\). Kromě posuvného pohybu hmotného středu kupředu se skruž otáčí, musíme tedy započítat také energii rotačního pohybu \(E_\mathrm{r}\).
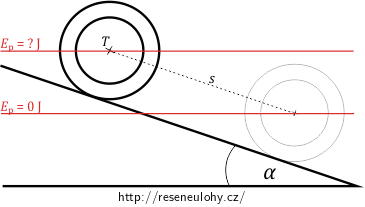
Nulovou hladinu potenciální energie zvolíme v místě, kde se nachází hmotný střed po uražení dráhy \(s\). Potenciální energie ve druhé situaci je tedy nulová. Ze zákona zachování mechanické energie víme, že celková mechanická energie v první situaci (skruž stojí na vrcholu svahu) musí být stejná jako v druhé situaci (skruž urazila dráhu \(s\)):
\[E_1=E_2,\]
\[E_\mathrm{p} = E_\mathrm{t} + E_\mathrm{r}.\tag{1}\]
Nyní se zaměříme na určení jednotlivých energií. Pro potenciální energii obecně platí
\[E_\mathrm{p}=mgh,\]
kde \(m\) je hmotnost tělesa, \(g\) tíhové zrychlení (zde jej uvažujeme rovno \(g=10\,\mathrm{m \cdot s^{-2}}\)) a \(h\) výška, ve které se těleso nachází vzhledem k nulové hladině potenciální energie. Tuto výšku snadno určíme z pravoúhlého trojúhelníku s přeponou \(s\) a s jedním ostrým úhlem o velikosti \(\alpha\) (viz obr. níže).
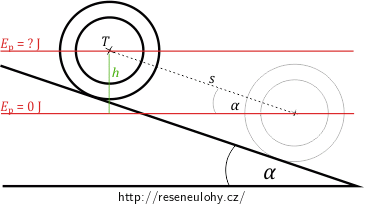
Tedy
\[h=s\,\sin{\alpha}.\]
Odtud dosazením do obecného vztahu pro potenciální energii získáme
\[E_\mathrm{p}=Mgs\,\sin{\alpha}.\]
Tím jsme vyjádřili levou stranu rovnice (1).
Pro kinetickou energii posuvného pohybu skruže platí
\[E_\mathrm{t}=\frac{1}{2}Mv^2,\]
kde \(M\) je hmotnost skruže a \(v\) je rychlost hmotného středu skruže (rychlost posuvného pohybu skruže), kterou chceme určit.
Zbývá vyjádřit energii rotačního pohybu, pro kterou obecně platí
\[E_\mathrm{r} = \frac{1}{2}J{\omega}^2,\]
kde \(J\) představuje moment setrvačnosti tělesa vzhledem k ose procházející hmotným středem a \(\omega\) je úhlová rychlost. Moment setrvačnosti skruže jsme určili v předchozí části úkolu. Víme tedy, že
\[J_\mathrm{skruž}=\frac{M(R^2+r^2)}{2}.\]
Protože chceme v rovnici pouze jednu neznámou, vyjádříme úhlovou rychlost rotačního pohybu pomocí okamžité rychlosti hmotného středu \(v\) (rychlosti posuvného pohybu skruže):
\[\omega=\frac{v}{R}.\]
Rotační energii tedy můžeme pro náš případ zapsat jako
\[E_\mathrm{r}=\frac{1}{2}\frac{M(R^2+r^2)}{2}{\left (\frac{v}{R}\right )}^2.\]
Nyní můžeme dosadit do rovnice (1) za obě strany:
\[Mgs\,\sin{\alpha} = \frac{1}{2}Mv^2 + \frac{M(R^2+r^2)}{4}\frac{v^2}{R^2}.\tag{2}\]
Ještě potřebujeme vyjádřit rychlost pomocí zrychlení. Víme, že hmotný střed urazí dráhu \(s\) za čas \(t\) a že se pohybuje rovnoměrně zrychleným pohybem se zrychlením \(a\). Víme, že pro takový pohyb platí:
\[s=\frac{1}{2}at^2,\]
\[v=at.\]
Odtud dosazením za čas do rovnice dráhy dostaneme vztah pro kvadrát rychlosti v závislosti na zrychlení:
\[v^2=2as.\tag{3}\]
Nyní můžeme dosadit z rovnice (3) do rovnice (2), upravit ji a vyjádřit zrychlení \(a\) hmotného středu skruže:
\[Mgs\,\sin{\alpha} = \frac{1}{2}2Mas + \frac{M(R^2+r^2)}{4}\frac{2sa}{R^2}, \]
\[g\,\sin{\alpha} = a + \frac{a(R^2+r^2)}{2R^2}, \]
\[g\,\sin{\alpha} = a\frac{(3R^2+r^2)}{2R^2},\]
\[a=\frac{2R^2 g\,\sin{\alpha}}{3R^2+r^2}.\]
Řešení b) – Pohybové rovnice
Načrtněme si situaci do obrázku. Tíhová síla \(\vec {F_\mathrm{G}}\) působí v hmotném středu skruže svisle dolů, tlaková síla svahu (podložky) \(\vec N\) působí v bodě dotyku skruže a svahu kolmo na podložku a třecí síla \(\vec {F_\mathrm{t}}\) působí proti pohybu skruže (který se děje směrem dolů ze svahu).
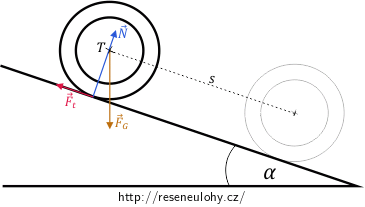
Skruž se pohybuje zrychleně, výslednice působících sil je tedy nenulová. Podle druhého Newtonova zákona platí:
\[\vec {F_\mathrm{výsledná}}=m\vec a,\]
kde \(a\) je velikost hledaného zrychlení hmotného středu.
Pohybovou rovnici potřebujeme přepsat skalárně. Soustavu souřadnic zvolíme podle obrázku. Tíhovou sílu rozložíme do směru souřadných os.
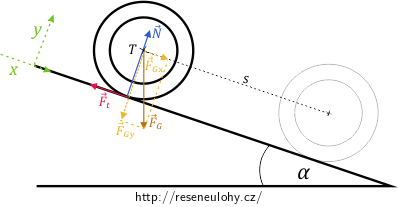
Nyní sestavme rovnice pro síly působící ve směru (či proti směru) příslušných os. Zrychlený pohyb způsobují pouze síly ve směru osy x, tímto směrem se skruž valí. Ve směru osy y skruž nijak neskáče, výslednice sil je v tomto směru rovna nule. Máme:
\[x: F_\mathrm{Gx}-F_\mathrm{t}=Ma,\]
\[y: N-F_\mathrm{Gy}=0.\]
Složky tíhové síly umíme vyjádřit pomocí pravoúhlého trojúhelníku s přeponou o velikosti \(F_\mathrm{G}\) a jedním ostrým úhlem o velikosti \(\alpha\):
\[F_\mathrm{Gx}=F_\mathrm{G}\,\sin{\alpha}=Mg\,\sin{\alpha},\]
\[F_\mathrm{Gy}=F_\mathrm{G}\,\cos{\alpha}=Mg\,\cos{\alpha}.\]
Rovnice pro směr y nám nedává žádnou důležitou informaci, dále tedy budeme pracovat pouze s rovnicí pro osu x. Dosazením získáváme
\[Mg\,\sin{\alpha}-F_t=Ma.\tag{4}\]
Abychom se dokázali „zbavit“ neznámé třecí síly, využijeme druhou impulsovou větu. Vyjádříme výsledný moment působících sil vzhledem ke středu otáčení skruže, tedy hmotnému středu. Tento bod je výhodný, protože je zároveň působištěm tíhové síly a také známe moment setrvačnosti skruže vzhledem k ose procházející tímto bodem. Pro velikost momentu síly (podle vztahu pro velikost vektorového součinu) máme
\[M=Fr_0\,\sin{\phi},\]
kde \(\phi\) je úhel, který svírají vektor síly \(\vec {F}\) a její polohový vektor \(\vec {r_0}\).
Velikost polohového vektoru tíhové síly je rovna nule, moment tíhové síly je tedy nulový. Podle obrázku vidíme, že otáčivé účinky normálové síly jsou také nulové, protože úhel mezi silou \(\vec N\) a vektorem \(\vec R\) je 180° a sinus 180° je roven nule.
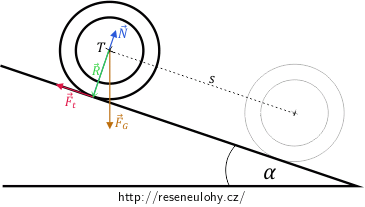
Třecí síla \(F_\mathrm{t}\) svírá s vektorem \(\vec R\) pravý úhel. Sinus pravého úhlu je roven 1, celkový moment síly je tedy roven
\[M_\mathrm{celkový}=F_\mathrm{t}R.\tag{5}\]
Celkový moment síly je nenulový, skruž se valí s nenulovým úhlovým zrychlením. Napíšeme pohybovou rovnici pro rotační pohyb
\[M_\mathrm{celkový}=J\xi,\]
kde \(J\) představuje moment setrvačnosti skruže, který jsme odvodili v řešení a), a \(\xi\) je úhlové zrychlení. To lze vyjádřit pomocí zrychlení \(a\) a poloměru otáčení, který je roven \(R\):
\[\xi =\frac{a}{R}.\]
Nyní dosadíme do rovnice (5) a spolu s rovnicí (4) tak získáme soustavu dvou rovnic o dvou neznámých, ze kterých již snadno určíme zrychlení \(a\) hmotného středu skruže:
\[F_\mathrm{t}R=J\frac{a}{R},\]
\[Mg\,\sin{\alpha}-F_t=Ma.\]
Z první rovnice vyjádříme třecí sílu \(F_\mathrm{t}\) a dosadíme do druhé rovnice:
\[F_\mathrm{t}=\frac{Ja}{R^2},\]
\[Mg\,\sin{\alpha}-\frac{Ja}{R^2}=Ma.\tag{6}\]
Rovnici (6) budeme dále upravovat, vyjádříme zrychlení \(a\) a dosadíme za moment setrvačnosti \(J\):
\[Mg\,\sin{\alpha}=a\left(M+\frac{J}{R^2}\right),\]
\[Mg\,\sin{\alpha}=a\left(M+\frac{M(R^2+r^2)}{2R^2}\right),\]
\[g\,\sin{\alpha}=a\left(\frac{(3R^2+r^2)}{2R^2}\right),\]
\[a=\frac{2R^2g\,\sin{\alpha}}{3R^2+r^2}.\]
Určili jsme zrychlení, s jakým se pohybuje hmotný střed skruže ze svahu.
Odpověď a)
Moment setrvačnosti skruže o vnitřním poloměru \(r\), vnějším poloměru \(R\) a hmotnosti \(M\) je
\[J=\frac{1}{2}M\left(R^2+r^2\right).\]
Odpověď b)
Zrychlení hmotného středu skruže je
\[a=\frac{2R^2 g\,\sin{\alpha}}{3R^2+r^2}.\]



