Centrifugal Force on the Equator
Task number: 929
Can a person who is standing on the Equator “fly away” by the effect of the centrifugal force?
The Earth equatorial radius is 6378 km, its angular velocity is 7.29·10−5 s−1. Assume that the person weighs 80 kg.
Notation
R = 6378 km Earth radius ω = 7.29·10−5 s−1 Earth angular velocity m = 80 kg mass of the person Fcf = ? centrifugal force From the tables:
ME = 5.97·1024 kg Earth mass G = 6.67·10−11 N m2 kg−2 gravitational constant Hint 1
Solve the task in the reference frame that rotates with the Earth. What forces act on the person? What can be said about the resultant force?
Hint 2 – magnitudes of the forces
Consider what the magnitudes of the forces would have to be for the person to fly away.
Calculate the magnitudes of the force of gravity and of the centrifugal force that act on the person on the Equator.
Complete solution
We calculate the task in the reference frame rotating with the Earth.
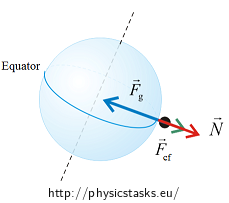
The person standing on the Earth is acted on by three forces in the non–inertial reference frame rotating with the Earth: the person is attracted with the force of gravity towards the Earth center, the person is lifted up by the centrifugal force (these two forces constitute the person’s weight) and the person is pushed up by the ground upon which he or she stands as a reaction to his or her weight.
The person is at rest with respect to the rotating Earth. The resultant of these forces is thus zero.
\[\vec{F}_{g}\,+\,\vec{N}\,+\,\vec{F}_{cf}\,=\,\vec{o}\]The magnitudes of the forces are:
\[F_{g} - N - F_{cf} = 0\]and thus:
\[F_{g} = N + F_{cf}\]If the person “took off” it would mean that the person would lose contact with the Earth and it would stop pushing him or her up. The magnitude of the force of gravity would be equal to the magnitude of the centrifugal force in that case. Let us calculate the magnitudes of both these forces.
Magnitude of the centrifugal force:
\[F_{cf} = m\frac{v^{2}}{R} = m\omega^{2}R = 80\,\cdot\, \left(7.29{\cdot}10^{-5}\right)^{2}\,\cdot \, 6378{\cdot}10^{3} \,\mathrm{N}\dot{=} 2.7\,\mathrm{N}\]Magnitude of the force of gravity:
\[F_{g} = G \frac{mM_{E}}{R^{2}} = 6.67{\cdot}10^{-11}\,\cdot\,\frac{80\, \cdot \, 5.97{\cdot}10^{24}}{\left(6378{\cdot}10^{3}\right)^{2}}\,\mathrm{N} \dot{=} 783.1\,\mathrm{N}\]Comparing the magnitudes of these two forces, we see that the person cannot fly away by the effect of the centrifugal force.
Answer
The person cannot fly away by the effect of the centrifugal force. The centrifugal force comprises only (−)0.3% of the person’s weight (the total force by which the person is pulled against the ground).What would be needed to get the opposite answer?
Let us try to calculate what the angular velocity of the rotation of the Earth would have to be to make the person “fly away”. The force of gravity and the centrifugal force then would have the same magnitude.
\[F_{cf} = F_{g}\] \[m\omega^{2}R = G\frac{mM_{E}}{R^{2}}\]Let us now express omega and calculate it in numbers:
\[\omega = \sqrt{G\frac{M_{E}}{R^{3}}} = \sqrt{6.67{\cdot}10^{-11}\,\cdot\,\frac{5.97{\cdot}10^{24}}{\left( 6378{\cdot}10^{3}\right)^{3}}}\, \mathrm{s^{-1}}\,\dot{=}\, 1.24{\cdot}10^{-3}\,\mathrm{s^{-1}}\] The peripheral velocity then would be: \[v = \omega R = 1.24{\cdot}10^{-3}\,\cdot\, 6378{\cdot}10^{3}\,\mathrm{m\, s^{-1}}\,\dot{=}\,7909\,\mathrm{m\, s^{-1}}\]Let us calculate in addition the duration of a single day (the period of rotation) under these circumstances.
\[T = \frac{2\pi}{\omega} = \frac{2\pi}{1.24{\cdot}10^{-3}}\,\mathrm{s} \,\dot{=}\,5067\,\mathrm{s} \,\dot{=}\, 1.4\,\mathrm{h} \]Weight and gravity
1) The difference between weight and gravity:
Weight is the name for the resultant force of the gravitational attraction (the force of the true gravity) and the centrifugal force. It thus has a slightly different magnitude than the gravity and it does not point directly to the center of the Earth. Because the differences between the magnitudes and directions of weight and gravity are tiny, they are often interchangeable (the centrifugal force comprises 0.3% of the weight on the Equator).
2) As we have said, weight is the resultant of the force of gravity and the centrifugal force. The centrifugal force depends on the radius of rotation which is different on the Equator and on the 50th circle of latitude (see the Figure; the Czech Republic lies there, for example) - it is slightly different on every latitude.
(Weight and gravity are identical on the poles, where no centrifugal force occurs. On the Equator, they differ only in magnitude, not in direction, because the centrifugal force directs exactly opposite to the force of gravity there. See also the solution of the task Spring Scale on the Pole and on the Equator).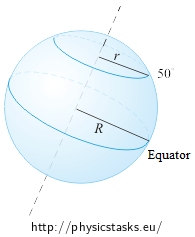
The true gravity and the weight are thus not the same on every point on the surface of the Earth. The so called “standard gravity”: gn = 9.80665 m s−2 (exactly) was thus accepted as a constant. It corresponds to the actual value of the acceleration of the free fall on the 45th circle parallel north at the sea level. It was accepted by the 3rd General Conference on Weights and Measures in 1901.
Link to a similar task