A rolling concrete ring
Task number: 4322
A concrete ring of a cylindrical shape and mass \(M\) is rolling down the slope without sliding. The slope forms an angle \(\alpha\) with the horizontal plane (see the figure below).
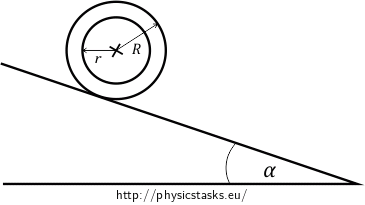
Analysis
We can view the concrete ring as a hollow cylinder with a thick wall. We assume the ring to be homogenous (its mass to be evenly distributed). We can determine the moment of inertia either from the following integral:
\[I=\int_V \rho r^2\mathrm{d}V,\]
or use the known formula for the moment of inertia of a cylinder.
We have two possible ways to determine the acceleration of the centre of mass of the ring. The first option is to use the law of conservation of mechanical energy: It holds for the ring that its total mechanical energy at the top of the slope is the same as after it travels a distance \(s\). The second option is to analyse the forces acting on the ring as well as the moments of those forces and write down the equations of motion. The resultant force, as well as the resultant moment of force, is nonzero. The ring is at rest at the top of the slope, and then it starts rolling down the slope with a uniformly accelerated motion. The centre of mass of the ring is moving straight and travels the distance \(s\). The motion of the ring as a whole, however, has both translational and rotational components. The resultant force on the ring as well as the resultant moment of force on the ring is nonzero.
Hint for a)
Use the general equation for the moment of inertia and consider if it is possible to imagine the ring divided into separate layers (convenient for calculating the integral). It can be handy to choose a layer in such a way that all its parts are equidistant from the axis of rotation of the ring. Draw an image of the situation, mark one such layer and write down its moment of inertia.
Hint for b)
We have two possible ways to determine the acceleration of the centre of mass of the ring. The first option is to use the law of conservation of mechanical energy: Choose the zero level of potential energy and the two situations in which you will compare the mechanical energies. Write down the expression of the energies in chosen situations. The second option is to analyse the forces acting on the ring as well as the moments of those forces and write down the equations of motion: Draw an image of the situation and mark the forces acting on the ring. If you are missing a specific value of a physical quantity (distance, angle, ...), you can work with it in general.
Solution of a)
The moment of inertia is defined as the following integral:
\[I = \int_{V} \rho r^2 \mathrm{d}V\]
where \(\rho\) is the density of the rigid body and \(V\) is its volume.
We imagine the concrete ring divided into separate layers (see figure below).
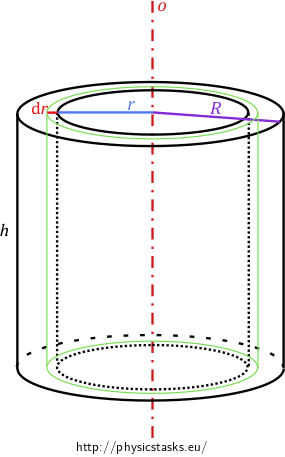
It holds for the moment of inertia \(\mathrm{d}I\) of one such layer (marked by green color in the figure):
\[\mathrm{d}I = r^2 \mathrm{d}m,\]
where \(\mathrm{d}m\) is the mass of the layer. We can express it in terms of the density \(\rho\) and the volume \(\mathrm{d}V\) of the layer:
\[\mathrm{d}m = \rho \mathrm{d}V = \rho 2h\pi r \mathrm{d}r.\]
The moment of inertia of one layer which has a shape of a hollow cylinder of a radius \(r\) is:
\[\mathrm{d}I = \rho 2h\pi r^3 \mathrm{d}r.\]
To determine the total moment of inertia, we sum up the moments of inertia of all layers. We go from radius \(r\) (inner radius of the ring) to radius \(R\) (outer radius of the ring):
\[I = \int_{r}^{R}2\rho h \pi r^3 \mathrm{d}r = 2\rho h \pi\left [ \frac{r^4}{4}\right ]_{r}^{R} = \frac{\rho h \pi}{2}\left(R^4-r^4\right ). \]
We express the density \(\rho\) of the concrete ring in terms of its total mass \(M\) and total volume \(V\). We calculate the total volume as the difference of the volume of two cylinders, one with radius \(R\) and the other with radius \(r\). It thus holds for the density \(\rho\):
\[\rho =\frac{M}{V}= \frac{M}{\pi R^2 h-\pi r^2 h}=\frac{M}{\pi h \left (R^2 -r^2\right )}.\]
Substituting the density \(\rho\) into integral and rearranging the expression, we get the final relation for the moment of inertia of the concrete ring. We use the mathematical formula \(A^2-B^2=\left(A-B\right)\left(A+B\right)\):
\[I = \frac{M}{\pi h \left (R^2 -r^2\right )} \frac{h \pi}{2}\left(R^4-r^4\right )=\frac{M}{ 2} \frac{\left(R^2-r^2\right) \left(R^2+r^2\right)}{\left (R^2 -r^2\right )} = \frac{1}{2} M \left(R^2+r^2\right).\]
Solution of b) – law of conservation of mechanical energy
We use the law of conservation of mechanical energy to solve the task. We consider two situations: The first is when the ring is located at the top of the slope (its cener of mass is at the highest point). It is at rest; it does not rotate, only its potential energy \(E_p\) is nonzero.
We choose the second situation to be after the ring travels a distance \(s\). It is moving at nonzero speed at that moment; it thus has nonzero kinetic energy of the translational motion \(E_t\). Besides the translational motion of the ring, it also rotates, so we have to take the kinetic energy of the rotational motion \(E_r\) into consideration.
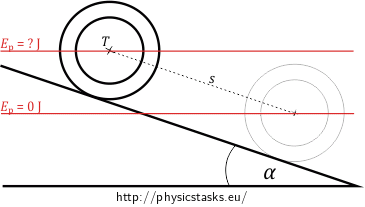
We set the zero point of potential energy in the centre of mass of the ring in the second situation. The total mechanical energy of the ring in the first situation (when the ring is at the top of the slope) must equal its total mechanical energy in the second situation (after the ring travels a distance \(s\)). It, therefore, holds that
\[E_1=E_2,\]
\[E_p = E_t + E_r.\tag{1}\]
We now want to determine the individual energies. The gravitational potential energy \(E_p\) is generally calculated as
\[E_p=mgh,\]
where \(m\) is the mass of the body, \(g\) is the gravitational acceleration (we assume it to be \(g=10\,\mathrm{m \cdot s^{-2}}\)), and \(h\) is the height of the body above the zero level of potential energy. We easily determine this height from a right triangle with the hypotenuse of length \(s\) and with one of the acute angles being \(\alpha\) (see figure below).
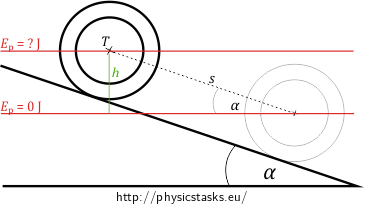
Thus:
\[h=s\,\sin{\alpha}.\]
Substituting into the general relation for the potential energy, we get:
\[E_p=Mgs\,\sin{\alpha}.\]
We have just determined the expression of the left side of the equation (1).
For the kinetic energy of the translational motion, it holds:
\[E_t=\frac{1}{2}Mv^2,\]
where \(M\) is the mass of the concrete ring and \(v\) is the speed of the centre of mass (which is the speed of the translational motion) we aim to determine.
It remains to express the energy of the rotational motion, for which we have the general equation:
\[E_r = \frac{1}{2}I{\omega}^2,\]
where \(I\) is the moment of inertia of a body with respect to the axis of rotation which passes through its centre of gravity, \(\omega\) is the angular speed. We determined the moment of inertia of the ring \(I\) in the previous part of the task and, therefore, we know:
\[I=\frac{M(R^2+r^2)}{2}.\]
To have only one unknown in the equation, we can express the angular speed in terms of the instantaneous speed \(v\) of the centre of mass (which is the speed of the translational motion):
\[\omega=\frac{v}{R}.\]
We now have for the energy of the rotational motion \(E_r\) of the ring:
\[E_r=\frac{1}{2}\frac{M(R^2+r^2)}{2}{\left (\frac{v}{R}\right )}^2.\]
We substitute the expressions of the energies in the equation (1):
\[Mgs\,\sin{\alpha} = \frac{1}{2}Mv^2 + \frac{M(R^2+r^2)}{4}\frac{v^2}{R^2}.\tag{2}\]
We need to express the speed in terms of acceleration. We know that the centre of mass travels a distance \(s\) in a time \(t\), and it moves with a uniformly accelerated motion which has an acceleration \(a\). We know that for such a motion the following holds:
\[s=\frac{1}{2}at^2,\]
\[v=at.\]
Substituting the time \(t\) into the equation for the distance \(s\), we get the relation for the square of the speed \(v^2\) in terms of the acceleration \(a\):
\[v^2=2as.\tag{3}\]
Finally, we substitute the equation (3) into the equation (2), rearrange it and express the acceleration \(a\) of the centre of mass of the concrete ring:
\[Mgs\,\sin{\alpha} = \frac{1}{2}2Mas + \frac{M(R^2+r^2)}{4}\frac{2sa}{R^2}, \]
\[g\,\sin{\alpha} = a + \frac{a(R^2+r^2)}{2R^2}, \]
\[g\,\sin{\alpha} = a\frac{(3R^2+r^2)}{2R^2},\]
\[a=\frac{2R^2 g\,\sin{\alpha}}{3R^2+r^2}.\]
Solution of b) – equations of motion
We draw a picture of the situation. The gravitational force \(\vec {F_G}\) is acting downward on the centre of mass of the ring, the pressure (normal) force of the slope \(\vec N\) is acting at the point of contact and is perpendicular to the surface of the slope, and the friction force \(\vec {F_f}\) is acting at the point of contact against the motion of the ring (the ring is moving down the slope).
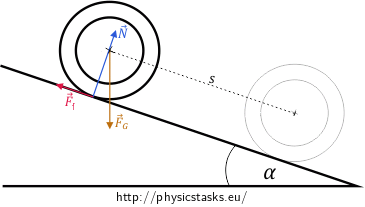
We know that the ring is moving with acceleration, which means that the resultant force on the ring is nonzero. From Newton’s second law of motion, it holds that
\[\vec {F_{total}}=m\vec a,\]
where \(\vec a\) is the acceleration of the centre of gravity which we aim to determine.
We want to rewrite the equation of motion in the scalar form: We choose the coordinate system as shown in the figure below and decompose the gravitational force into the directions of the coordinate axes.
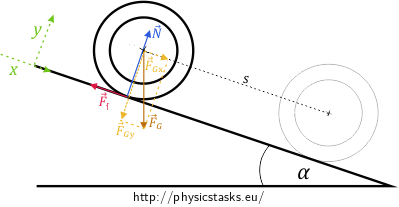
We write down the equations of motions for the forces acting in directions of the coordinate axes. The forces acting in the direction of the x-axis cause the ring to accelerate. The ring does not move in the direction of the y-axis (it does not bounce when rolling down the slope), which means that the resultant force in this direction is zero. We have:
\[x: F_{Gx}-F_f=Ma,\]
\[y: N-F_{Gy}=0.\]
We use a right triangle with a hypotenuse of length \(F_G\) and with one of the acute angles being equal to \(\alpha\) to express the components of gravitational force:
\[F_{Gx}=F_G\,\sin{\alpha}=Mg\,\sin{\alpha},\]
\[F_{Gy}=F_G\,\cos{\alpha}=Mg\,\cos{\alpha}.\]
The equation for the forces in the direction of the y-axis does not give us any important information; we will use only the equation for the forces in the direction of the x-axis. Substituting the expression of \(F_{Gx}\), we get:
\[Mg\,\sin{\alpha}-F_f=Ma.\tag{4}\]
To “get rid of” the unknown friction force in the equation, we use the angular momentum theorem. We express the resultant moment of the acting forces with respect to the centre of mass of the ring (which lays on its axis of rotation). This reference point is convenient because it is also the point of application of the gravitational force and the moment of the gravitational force is then zero. It holds for the magnitude of a moment of a force (from the relation for the magnitude of the cross product):
\[M=Fr_0\,\sin{\phi},\]
where \(\phi\) is the angle formed by the vector of a force \(\vec {F}\) and the position vector for this force \(\vec {r_0}\).
The moment of the gravitational force is zero (because its position vector is zero). You can see from the figure below that the moment of the normal force \(\vec N\) is also zero because it forms an angle of 180° with its position vector \(\vec R\) and the sine of 180° is zero.
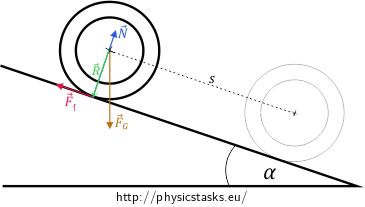
The friction force \(F_f\) forms a right angle with its position vector \(\vec R\). The sine of a right angle is equal to 1 and, therefore, we get for the resultant moment of force on the ring:
\[M_{total}=F_fR.\tag{5}\]
The total moment of force is nonzero as the ring is rolling with a nonzero angular acceleration. We write down an equation of motion for the rotational motion:
\[M_{total}=I\xi,\]
where \(I\) is the moment of inertia of the ring, which we derived in the solution of a); \(\xi\) is the angular acceleration which can be expressed in terms of the acceleration \(a\) of the translational motion of the ring and the radius of the ring which is equal to \(R\):
\[\xi =\frac{a}{R}.\]
Substituting into the equation (5), we get:
\[F_fR=I\frac{a}{R}\]
and together with the equation (4), we get a system of two equations with the two unknowns:
\[F_fR=I\frac{a}{R},\]
\[Mg\,\sin{\alpha}-F_f=Ma.\]
We can now easily express the acceleration \(a\) of the centre of mass of the ring: We express the friction force \(F_f\) from the first equation, and substituting it into the other equation, we get:
\[F_f=\frac{Ia}{R^2},\]
\[Mg\,\sin{\alpha}-\frac{Ia}{R^2}=Ma.\tag{6}\]
We continue in transforming the equation (6); we express the acceleration \(a\) and substitute the moment of inertia \(I\):
\[Mg\,\sin{\alpha}=a\left(M+\frac{I}{R^2}\right),\]
\[Mg\,\sin{\alpha}=a\left(M+\frac{M(R^2+r^2)}{2R^2}\right),\]
\[g\,\sin{\alpha}=a\left(\frac{(3R^2+r^2)}{2R^2}\right),\]
\[a=\frac{2R^2g\,\sin{\alpha}}{3R^2+r^2}.\]
We have determined the acceleration with which the centre of mass of the concrete ring rolls down the slope.
Answer for a)
The moment of inertia \(I\) of the concrete ring of an inner radius \(r\), outer radius \(R\) and a mass \(M\) is:
\[I=\frac{1}{2}M\left(R^2+r^2\right).\]
Answer for b)
The acceleration \(a\) of the centre of mass of the concrete ring is:
\[a=\frac{2R^2 g\,\sin{\alpha}}{3R^2+r^2}.\]



