Yo-yo
Task number: 4321
A yo-yo is made from two sheet metal disks of density \(\rho\), thickness \(d\), and radius \(R\). An axle of radius \(r\) connects the two disks together.
Determine the moment of inertia \(I\) of the yo-yo with respect to its rotational axis of symmetry. Assume that the mass and the moment of inertia of the axle are negligible.
The string wound on the axle is of a length \(l\), and its thickness is negligible. What is the acceleration of the yo-yo when it unwinds downward?
What is the magnitude of the tensile force with which the string acts on the yo-yo?
Analysis
When we neglect the mass and the moment of inertia of the axle, we can look at the yo-yo as two disks of the same weight. We will derive the moment of inertia of the yo-yo from the known equation for the moment of inertia of a disk. We will calculate the mass of one disk from its density and volume.
The acceleration of the yo-yo with which it unwinds downward is related to the forces acting on it, i.e., the gravitational force and the tensile force of the string. (We assume the player releases the yo-yo freely; there is thus no force of his throw.) The motion of the yo-yo is composed of two parts: The first is the accelerated translational motion, and the second is the rotation of the yo-yo around its axis of symmetry. To determine the acceleration of the translational component of motion of the yo-yo, we will write down the equation of motion for the forces acting on the yo-yo and for the moments of the forces acting on the yo-yo with respect to its centre of gravity.
We can look at the situation from a different point of view, taking the law of conservation of mechanical energy into consideration. In that case, we choose the zero level of potential energy and compare the total mechanical energy of the yo-yo in two situations of our choice.
Hint for a)
We neglect the mass and the moment of inertia of the axle; we can thus imagine the yo-yo as two homogenous and thick disks. Recall the equation for the moment of inertia of a disk. How will the equation look in our case? Pay attention to the correct masses.
Solution of a)
A moment of inertia of one homogenous disk of a mass \(m_1\) and of a radius \(R\) is:
\[I_{disk}=\frac{1}{2} m_1R^2.\]
The yo-yo is composed of two such disks; therefore, we will multiply the above moment of inertia \(I_{disk}\) by two. We can express the mass of one disk as a product of its volume \(V_{disk}\) and its density, which is the same as the density \(\rho\) of the yo-yo. We get:
\[I=2\,I_{disk}= m_1R^2=\rho\,V_{disk}R^2.\]
We calculate the volume of one disk from the equation for a volume of a cylinder:
\[V_{disk}=\pi R^2 d,\]
where \(d\) is the thickness of one disk of yo-yo.
For the moment of inertia of the yo-yo, we get:
\[I=\rho\,\pi R^2 dR^2= \pi \rho R^4d. \]
To express the moment of inertia of the yo-yo in terms of its mass \(m\), we substitute for the density \(\rho\) into the equation. The density \(\rho\) is a quotient of the mass of the yo-yo \(m\) divided by its total volume \(V\) (volume of both disks together):
\[I=\pi R^4 d \frac{m}{2\pi R^2 d}.\]
We rearrange the expression on the right side of the equation and get the final expression of the moment of inertia of the yo-yo \(I\):
\[I= \frac{1}{2}mR^2.\]
Hint for b)
We can determine the acceleration with which the yo-yo unwinds downward from the forces acting on it. Draw a picture of the yo-yo and all the forces acting on it. (We assume the player releases the yo-yo freely; there is thus no force of his throw.) Write down the equation of motion for the translational motion of the yo-yo, do the same for its rotational motion.
The second possibility to determine the acceleration with which the yo-yo unwinds downward is to use the law of conservation of the mechanical energy. In this case, choose the zero level of potential energy and compare the total mechanical energy of the yo-yo in two situations of your choice.
Solution of b) – equations of motion
To determine the acceleration of the yo-yo from the analysis of the forces acting on it and writing down the equations of motion, we start with drawing a picture of the situation. The forces acting on the yo-yo are the gravitational force \(\vec {F_G}\) which is acting on the centre of gravity of the yo-yo, and the tensile force of the string \(\vec T\) which is acting upward on the point where the string unwinds from the axle.
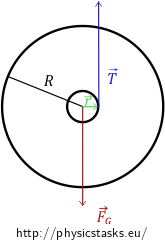
The yo-yo is moving downward with acceleration, which means that the resultant force is nonzero. It holds:
\[\vec {F_G}+\vec {T} = m\vec a,\]
where \(\vec a\) is the acceleration which we aim to determine. We rewrite the equation of motion in the following scalar form:
\[F_G-T=ma.\]
We substitute for the gravitational force \(F_G\):
\[mg-T=ma.\tag{1}\]
We do not know how to express the tensile force of the spring \(T\) yet. We need one more equation which we will get from the angular momentum theorem. We will determine the moments of the forces with respect to the centre of gravity of the yo-yo because it is also the point of application of the gravitational force \(\vec {F_G}\). The magnitude of the position vector for the gravitational force \(\vec {F_G}\) is zero and thus, also the moment of gravitational force is zero. It remains to use the moment of the tensile force of the spring \(T\). We get the angular momentum theorem in the following form:
\[\vec r × \vec T = I \vec\epsilon,\]where \(\vec r\) is the position vector for the tensile force, \(I\) is the moment of inertia of the yo-yo, and \(\vec \epsilon\) is its angular acceleration.
As the tensile force \(\vec T\) is tangential to the axle of the yo-yo, there is a right angle between the position vector \(\vec r\) and the tensile force \(\vec T\). It thus holds for the magnitude of the cross product:
\[|\vec r × \vec T|=rT sin{\alpha}=rT.\]
We get the following scalar form of the angular momentum theorem:
\[Tr=I\epsilon.\]
We can express the angular acceleration \(\epsilon\) as follows:
\[\epsilon = \frac{a}{r}.\]
We get:
\[Tr=J\frac{a}{r}.\tag{2}\]
Substituting for the tensile force \(T\) from the equation (2) to the equation (1), we get:
\[mg-ma=I\frac{a}{r^2}.\]
We express the acceleration of the yo-yo \(a\); then we substitute for the moment of inertia \(I\):
\[a\left (m+\frac{I}{r^2} \right)=mg,\]
\[a=\frac {mg}{\left (m+\frac{I}{r^2} \right)},\]
\[a=\frac {g}{\left (1+\frac{I}{mr^2} \right)}=\frac {g}{\left (1+\frac{mR^2}{2mr^2} \right)}=\frac {g}{\left (1+\frac{R^2}{2r^2} \right)}.\]
Rearranging the expression, we get:
\[a=\frac {2gr^2}{2r^2+R^2}.\]
Solution of b) – law of conservation of mechanical energy
We will use the law of conservation of mechanical energy and compare the total mechanical energy of the yo-yo in two situations. We choose the situations as follows: First is when the yo-yo is at rest in the player’s hand, and second is when the whole string of the length \(l\) is unwound (the kinetic energy of the yo-yo is maximal in this situation). We choose the zero level of the potential energy the centre of gravity of the yo-yo in the second situation (when it is closest to the ground). From the equality of the total mechanical energies of yo-yo in those two situations, we, therefore, get:
\[E_p = E_t+E_r,\tag{3}\]
where \(E_p\) is the potential energy of the yo-yo in the first situation, \(E_t\) is the kinetic energy of its translational motion in the second situation, and \(E_r\) is the kinetic energy of its rotational motion in the second situation.
It holds for the energies:
\[E_p=mgl,\]
\[E_t=\frac{1}{2}mv^2,\]
\[E_r=\frac{1}{2}I\omega^2,\]
where the speed \(v\) stands for the speed of translational motion and \(\omega\) stands for the angular speed of the rotational motion.
We can express the angular speed \(\omega\) as the quotient of the speed \(v\) divided by the radius \(r\) of the axle from which the string unwinds.
We substitute the above relations into the equation (3):
\[mgl=\frac{1}{2}mv^2+\frac{1}{2}I\frac{v^2}{r^2}.\tag{4}\]
We need to express the speed \(v\) in terms of the acceleration \(a\). We know that the translational motion of the yo-yo is uniformly accelerated and that the length of its path is \(l\). For the speed and path of uniformly accelerated motion, it holds:
\[v=at,\]
\[l=\frac{1}{2}at^2.\]
We get for the square of the speed \(v^2\):
\[v^2=2la.\]
Substituting \(v^2\) into the equation (4), we get an equation of one unknown \(a\):
\[mgl=\frac{1}{2}m2la+\frac{1}{2}I\frac{2la}{r^2}.\]
Rearranging the equation and expressing the acceleration \(a\), we get:
\[mg=ma+a\frac{I}{r^2},\]
\[mg=a\left(m+\frac{I}{r^2}\right),\]
\[a=\frac{g}{1+\frac{I}{mr^2}}.\]
Substituting for the moment of inertia \(I\) from the first part of this task, we can express the acceleration in the following form:
\[a=\frac{g}{1+\frac{R^2}{2r^2}}=\frac {2gr^2}{2r^2+R^2}.\]
Hint for c)
Have a look on the equation of motion we found in the solution of b). You can easily determine the tensile force of the spring \(T\) from it.
Solution of c)
In the solution of b), we found the equation of motion (1) for the forces acting on the yo-yo. In the same part of the task, we also expressed the acceleration of the yo-yo \(a\) with which it unwinds downward. We can express the tensile force \(T\) from the equation of motion (1) and substitute for the acceleration \(a\):
\[mg-ma=T,\]
\[T=m\left(g-a\right)=m\left(g-\frac{2gr^2}{2r^2+R^2}\right)=\left(\frac{mgR^2}{2r^2+R^2}\right).\]
Expressing the tensile force of the spring \(T\) in terms of the moment of inertia \(I\), we get:
\[T=\frac{mg}{1+\frac{mr^2}{I}}.\]
Answer for a)
The moment of inertia of the yo-yo is:
\[ I=\pi \rho R^4d.\]It can be expressed in terms of the mass \(m\) of the yo-yo and its radius \(R\):
\[I= \frac{1}{2}mR^2.\]
Answer for b)
The yo-yo unwinds downward with the acceleration:
\[a=\frac {2gr^2}{2r^2+R^2}.\]
Answer for c)
The string acts on the yo-yo with the tensile force \(T\) of the following magnitude:
\[T=\left(\frac{mgR^2}{2r^2+R^2}\right)=\frac{mg}{1+\frac{mr^2}{I}}.\]



