Collection of Solved Problems in Physics

Otto Cycle Efficiency

Task number: 1288

• Hint

  a) Consider whether it is possible to calculate the work performed by the gas in one cycle of the cyclic process without using the formulas for work.

  b) Try adjusting the equation for an ideal gas undergoing an adiabatic process so that it involves the thermodynamic temperature.

• Solution of Hint b)

  The equation for an ideal gas undergoing an adiabatic process is in the form pV^κ = C = konst., where C is a constant and κ is the Poisson’s constant. Now we evaluate the pressure from the equation of state for an ideal gas.

  \[\frac{pV}{T} = K \quad\Rightarrow\quad p = \frac{T}{V} K, \]

  where K is again a constant.

  Now we substitute this evaluated pressure into the first equation and next we transfer the constants (C and K) to one side:

  \[pV^{\kappa} = C \quad\Rightarrow\quad\frac{T}{V}V^{\kappa} K = C \quad\Rightarrow \quad TV^{\kappa - 1} = \frac{C}{K} = \mathrm{konst.}\]

• Analysis

  In order to express the efficiency of the Otto cycle, we need to evaluate the work performed by the gas during one cycle and the heat which the gas received during this cycle. Efficiency is the proportion of the work and the supplied heat.

  For a cyclic process, the change in the total internal energy of the gas during one cycle is zero. This occurs because the gas is in the same state both at the beginning and at the end of each cycle, and because the internal energy is a state function (the change depends only on the initial and the final state, not on the way the process was performed). According to the First Law of Thermodynamics, the work done by the gas can be expressed as a difference between the heat supplied and the heat released.

  Given the fact that during the adiabatic processes the heat is not transferred, the gas can therefore receive the heat only during the isochoric heating and releases the heat during the isochoric cooling.

  We will determine the heat supplied and released by using the molar heat capacity at constant volume. After determining both heats, we can finally express the efficiency of the Otto cycle. To express the efficiency with the compression ratio and the Poisson’s ratio we will use the modified equation for an ideal gas during an adiabatic process with the substituted pressure from the equation of the state of an ideal gas. Therefore it will include the thermodynamic temperature instead of the pressure.

• Solution

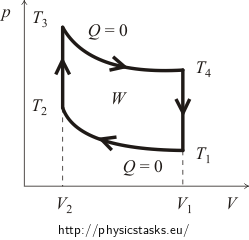
  At the beginning, it is usually necessary to get the idea of the pV diagram of the cycle. For this we will trace the curves of the isochoric and adiabatic processes. The approximate graph of the Otto cycle is shown in the following figure.

  

  The efficiency η of the cycle is defined as

  \[\eta = \frac{W}{Q_{sup}},\]

  where W is the work performed by the gas during one cycle minus the work performed by the external forces (in the diagram it is represented by the surface of the area defined by the lines of the cycle!) and Q_sup is the heat supplied to the system during the cycle.

  The work W can be calculated by using the relationship between the pressure and the volume during an adiabatic expansion and compression (the work performed during an isochoric process is of course zero). In this task, however, it will be better to use the fact that the total change in the internal energy per cycle must be equal to zero (we get back to the same state as at the beginning, therefore the temperature and hence the internal energy remain the same!). According to the First Law of Thermodynamic, the work performed by the gas can be expressed as the difference between the heat Q_sup supplied and the heat Q_rel released. The formula for the efficiency of the cycle is therefore in the form of

  \[\eta = \frac{W}{Q_{sup}} = \frac{Q_{sup}-Q_{rel}}{Q_{sup}}.\]

  First, we will calculate the supplied heat Q_sup. It is clear that during the adiabatic process there is no heat exchange and during the isochoric cooling the heat is released. This means that the heat will be supplied only during the isochoric heating from the temperature T₂ to the temperature T₃. The amount of this heat can be expressed in the variables of the amount of substance n of the gas and its molar heat capacity C_V as follows:

  \[Q_{sup} = nC_{V}\left( T_{3}-T_{2} \right) \]

  We will express the amount of the released heat Q_rel in much the same way. We already know that the heat is released only during the isochoric cooling from the temperature T₄ back to the initial temperature T₁. It is true that:

  \[Q_{od} = nC_{V}\left( T_{4}-T_{1} \right) \]

  Now we substitute these formulas into the formula of the cycle efficiency and we immediately obtain:

  \[\eta = \frac{Q_{sup}-Q_{rel}}{Q_{sup}} = \frac{nC_{V}\left( T_{3}-T_{2} \right) - nC_{V}\left( T_{4}-T_{1} \right)}{nC_{V}\left( T_{3}-T_{2} \right)} = \] \[=1 - \frac{T_{4} - T_{1}}{T_{3} - T_{2}}\]

  Now we will need to express the temperature differences by using the given compression ratio

  \[r=\frac{V_{1}}{V_{2}}\]

  and the Poisson’s ratio κ.

  To do so, we will use the equation for an ideal gas undergoing an adiabatic process (the Poisson’s law) pV^κ = C = konst., where C is a constant. Now we evaluate the pressure from the state equation of an ideal gas

  \[\frac{pV}{T} = K \quad\Rightarrow\quad p = \frac{T}{V} K\]

  which we substitute in the Poisson’s law. Now we transfer the constants (C and K) to one side

  \[pV^{\kappa} = C \quad\Rightarrow\quad\frac{T}{V}V^{\kappa} K = C \quad\Rightarrow \quad TV^{\kappa - 1} = \frac{C}{K} = \mathrm{konst.}\]

  Now we apply this Poisson’s law for both adiabatic processes. For the adiabatic expansion we obtain the relation

  \[T_{4}V_{1}^{\kappa - 1} = T_{3}V_{2}^{\kappa - 1},\]

  And for the adiabatic compression we obtain

  \[T_{1}V_{1}^{\kappa - 1} = T_{2}V_{2}^{\kappa - 1}.\]

  Now we subtract the second equation from the first one and factor out V₁^{κ − 1} on one side and V₂^κ − 1 on the other. We obtain:

  \[\left( T_{4}-T_{1}\right) V_{1}^{\kappa -1} = \left( T_{3}-T_{2}\right) V_{2}^{\kappa -1} \Rightarrow \frac{T_{4}-T_{1}}{T_{3}-T_{2}} = \left( \frac{V_{2}}{V_{1}}\right) ^{\kappa - 1} \Rightarrow\] \[\Rightarrow \frac{T_{4}-T_{1}}{T_{3}-T_{2}} = \left( \frac{1}{r}\right) ^{\kappa - 1}\]

  We can see that we have actually managed to express the temperature differences by using the given values. Now we substitute this relation into the formula for the efficiency and we get the final equation:

  \[\eta = 1-\frac{T_{4}-T_{1}}{T_{3}-T_{2}} = 1-\left( \frac{1}{r}\right) ^{\kappa - 1}\] \[\eta = 1-r^{1-\kappa}\]

• Answer

  The Otto cycle efficiency is therefore given by the relation

  \[\eta = 1-r^{1-\kappa}.\]