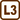Heating of Steel Bar
Task number: 2224
A steel bar is fixated at both ends and is not tensed at 10 °C. What is the tension in the bar going to be if we rise its temperature to 100°C?
List of known information
t1 = 10 °C original temperature before tensing t2 = 100 °C temperature after heating From tables:
E = 210·103 MPa Young’s modulus of steel α = 1.2·10-5 K−1 steel’s thermal coefficient of length extension σ = ? Pa tension in bar after heating Analysis
The bar’s length changes with temperature difference, however, the bar is fixated and can’t move. Tension will thus be created in the bar. We can express the bar’s relative extension if we find the bar’s length dependence on temperature. After that we just need to write the relation between the tension and the relative extension of the bar.
Hint
Recall how the bar’s extension depends on the temperature difference. Express the relative extension of the bar during the given temperature difference. Also use the relation giving the dependence between tension and relative extension of the bar.
Solution
The bar’s extension dependence on temperature is given by the following relation:
\[\Delta l\,=\, l_1 \alpha \left({t_2-t_1}\right),\]where l1 is the original length of the bar at temperature t1.
The relative extension of the bar is then equal to:
\[\varepsilon\,=\,\frac{\Delta l}{l_1}\,=\,\alpha \left({t_2-t_1}\right).\tag{1}\]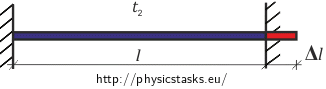
The bar is fixated so it must preserve its length. For that, pressure tension is required:
\[\sigma\,=\,E\varepsilon.\tag{2}\]All we need to do is substitute (1) into (2):
\[\sigma\,=\,E\alpha \left({t_2-t_1}\right).\tag{3}\]After numeric substitution into (3), we get:
\[\sigma\,=\,210{\cdot}10^{9}\cdot1.2{\cdot}10^{-5}\cdot\left({100-10}\right)\mathrm{Pa}\,=\,22.68{\cdot}10^{7} \mathrm{Pa}.\]Answer
Tension in the bar after heating is:
\[\sigma\,=\,22.68{\cdot}10^{7} \mathrm{Pa}.\]