Collection of Solved Problems in Physics

Mine Shaft Elevator

Task number: 1289

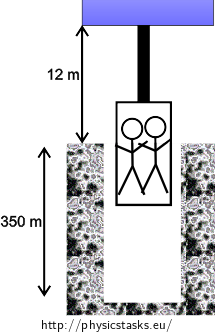
• Figure of the lift in the mine shaft

  

• Numerical values

  d = 2.5 cm = 0.025 m	the diameter of the rope
  m = 650 kg	hthe mass of the cabin with people
  h1 = 12 m	the distance of the elevator motor from the surface
  h2 = 350 m	the depth of the shaft
  Δl1 = ?	the extension of the rope in case a)
  Δl2 = ?	the extension of the rope in case b)

  Other necessary values:

  g = 9.81 ms−2	the acceleration of gravity
  E = 210 GPa = 2.1×1011 Pa	the Young’s modulus for steel
  σE = 400 MPa = 4×108 Pa	the elastic limit of steel

• Analysis

  The cabin applies force with its weight on the rope, making it extend. If this force is not too large, the extension is directly proportional to the force. And if the force ceases to act, the cable returns to its original length. This is true only if the normal stress (the ratio between the size of the applied force and the cross-sectional area of the material) does not exceed the elastic limit. This is called the elastic deformation, which is described by the Hook’s Law. It involves the Young’s modulus of the given material, which is a constant of proportionality between the relative extension and the normal stress, which is generated by the force.

• Solution

  The cabin applies force with its weight on the rope. The force is the same as the force of gravity \(F_G=mg\) applied on the cabin. This force generates a normal stress σ in the rope:

  \[\sigma = \frac {F_G}{S} = \frac{ mg}{ \pi \frac {d^2}{4}} = \frac{4mg}{\pi d^2} = \frac{4\cdot{650} \cdot{9.81}}{\pi \cdot{0.025^2}} \,\mathrm Pa \dot= 13\cdot{10^6} \,\mathrm Pa = 13 \,\mathrm MPa\]

  We can see that the generated normal stress is less than the elastic limit of steel \(\sigma_E=400\,\mathrm{MPa}\), and thus we can use the Hook’s Law to calculate the extension of the rope:

  \[\sigma = E \varepsilon ,\]

  where E is the Young’s modulus of steel and ε is the relative extension of the rope, for which the following formula applies:

  \[ \varepsilon = \frac {\Delta l}{l}.\]

  Now we substitute for the normal stress σ and for the relative extension ε into the Hook’s Law and express the extension Δl of the rope:

  \[ \frac {4mg}{\pi d^2}=E \frac {\Delta l}{l} \Rightarrow \Delta l = \frac {4mgl}{\pi d^2 E}.\]

  Now we insert the numerical values. We substitute the value h₁ for the length of the rope in the case of the elevator at the surface and we get:

  \[ \Delta l = \frac {4mgl}{\pi d^2 E}= \frac{4 \cdot {650} \cdot{9.81} \cdot{12}}{\pi \cdot{0.025^2} \cdot 2.1 \cdot{10^{11}}} \,\mathrm m \dot= 7.4\cdot{10^{-4}} \,\mathrm m = 0.74 \,\mathrm mm.\]

  In the case of the elevator at the bottom of the shaft, the length l of the rope equals to the sum of the depth of the shaft h₁ and the distance of the elevator motor from the surface h₂, so that:

  \[ \Delta l = \frac {4mg(h_1 + h_2)}{\pi d^2 E}= \frac{4 \cdot{650} \cdot{9.81} \cdot{(12+350)}}{\pi \cdot{0.025^2} \cdot{2.1} \cdot{10^{11}}} \,\mathrm m \dot= 0.022 \,\mathrm m =2.2 \,\mathrm cm.\]

• Answer

  If the elevator is at the surface, the rope is extended by approximately 0.74 mm. If the elevator descends to the bottom of the shaft, the extension of the rope is approximately 2.2 cm.