Small cork boat
Task number: 1292
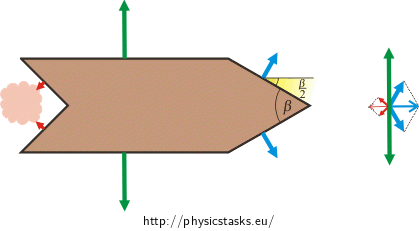
A 50 g weighing cork boat floats on the water surface. The boat has a shape as shown in the picture. A drop of detergent is added to the spot A. The surface tension of the mixture of water and detergent has a quarter value compared to pure water.
a) Explain what happens to the boat and why.
b) What is the magnitude of the force affecting the boat and what acceleration would the boat move with, if we neglected the friction force of the water?
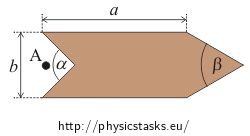
Consider the following dimensions of the boat:
a = 20 cm, b = 5 cm, α = 90° and β = 60°.
Hint
The water acts on boat edges with surface force due to the surface tension. This force points horizontally and perpendicularly to the boat. Its magnitude is proportional to the surface tension and the length of the boat edge.
Draw the forces acting on each of the boat edges and think over where their resultant points.
Notation
a = 20 cm, b = 5 cm, α = 90°, β = 60° boat dimensions m = 50 g = 0.05 kg boat weight σm = σv relation between surface tensions of water with the detergent and pure water From tables: σv = 73 mN m-1 pure water surface tension Analysis and solution of part a)
Due to the surface tension, the surface of liquid acts at its border on a container or an object standing out of the liquid by the surface force. This force is always perpendicular to the edge of the surface. We can also imagine that the liquid tries to “reduce its surface”. The acting force is proportional to the surface tension (constant characterizing the fluid) and the length at which it acts.
In the vertical direction, the boat is affected by gravitational force and buoyancy force. Because the boat floats on the surface, these forces equal in magnitude and point to the opposite directions. The water surface acts on the boat with surface forces in the horizontal direction (see the figure below).
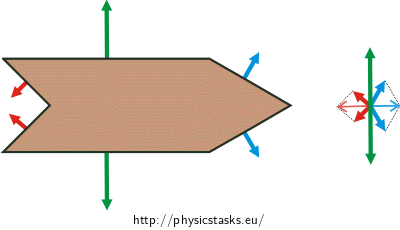
If the boat is surrounded by water on all sides, the resultant of all these forces is zero and the boat does not move. This will be discussed in detail in the numerical solution section.
If we place the drop of the detergent behind the boat, the local surface tension is reduced and thus also the forces acting on the rear side of the boat. Therefore the forces acting on the front side of the boat prevail and cause a motion in the forward direction. The surface forces acting on the boat are summarized in the following figure and the resultant force is found so that we can calculate the acceleration caused by this force according to the boat weight.
Solution of part b)
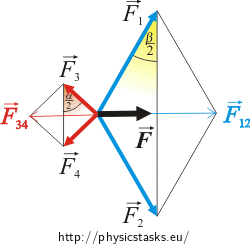
It is evident from the figures shown in the analysis section that the surface forces acting on the “inclined boat parts” are crucial so that we can calculate the resultant surface force acting on the boat. The forces are summarized into the detailed figure below.
The resultant of the “blue” forces \(\vec{F}_1\) and \(\vec{F}_2\) affecting the front side of the boat is marked \(\vec{F}_{12}\). Analogously, the resultant of the “red” forces \(\vec{F}_3\) and \(\vec{F}_4\) affecting the back side of the boat will be referred as \(\vec{F}_{34}\).
The task is to calculate the resultant of these forces, i.e. the force F:
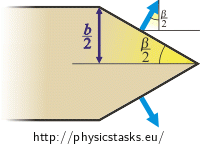
\[\vec{F}\,=\,\vec{F}_1\,+\vec{F}_2\,+\,+\vec{F}_3\,+\,\vec{F}_4\,=\,\vec{F}_{12}\,+\,\vec{F}_{34}\]The forces \(\vec{F}_1\) and \(\vec{F}_2\) act on the side of the boat with the following length: \[\frac{\frac{b}{2}}{\cos \frac{\beta}{2}}\,.\] Therefore for their sizes:
\[F_1\,=\,F_2\,=\, \sigma_v \, \frac{b}{ 2 \cos \frac{\beta}{2}}\] \[F_{12}\,=\, 2F_1 \,\cos \frac{\beta}{2} \,=\, 2\sigma_v \, \frac{b}{ 2 \cos \frac{\beta}{2}}\,\cos \frac{\beta}{2}\,=\, 2\sigma_v b\]Similarly, the magnitude of the forces \(\vec{F}_3\) and \(\vec{F}_4\) and their resultant \(\vec{F}_{34}\) can be expressed. One can not forget, that apart from a different angle, the surface tension must be substituted, because there is the detergent solution behind the boat.
\[F_3\,=\,F_4\,=\, \sigma_m \, \frac{b}{ 2 \cos \frac{\alpha}{2}}\] \[F_{34}\,=\, 2F_3 \,\cos \frac{\alpha}{2} \,=\, 2\sigma_m \, \frac{b}{ 2 \cos \frac{\alpha}{2}}\,\cos \frac{\alpha}{2}\,=\, 2\sigma_m b\]The forces \(\vec{F}_{12}\) and \(\vec{F}_{34}\) act in opposite directions, therefore the resultant force magnitude is given by the subtraction of their magnitudes:
\[F \,=\, F_{12}\,-\, F_{34}\, =\, \sigma_v b \,-\, \sigma_m b \,=\, (\sigma_v - \sigma_m ) b \]It is clearly evident from this relation, that the resultant of the acting forces is zero before the detergent drop is added (because in this moment the surface tensions behind and in front of the boat are equal). Therefore the boat remains static.
When we recall the specified values:
\[F \,=\, (\sigma_v - \frac{1}{4}\sigma_v ) b\,=\, \frac{3}{4}\sigma_v b \,=\, \frac{3}{4}\,\cdot \, 0.073 \,\cdot\, 0.05 \, \mathrm{N}\] \[F \,\dot=\, 2.7\, \mathrm{mN}\]A value of the boat acceleration caused by this force is determined by the Newton’s second law:
\[a \,=\, \frac{F}{m}\,=\,\frac{3 \sigma_v b}{4m}\,=\,\frac{3\,\cdot\,0.073\,\cdot\,0.05}{4\,\cdot \,0.05}\, \mathrm{m\,s}^{-2}\] \[a \,\dot=\, 0.05\,\mathrm{m\,s}^{-2}\]Answer
After the detergent drop is added near the boat back side, the boat is affected by forward force of about 2.7 mN and the boat starts to move. In case of zero friction, the force would give an acceleration of 0.05 m s-2 to the boat. However, there is considerable friction force of water and thus the real boat acceleration is markedly lower.