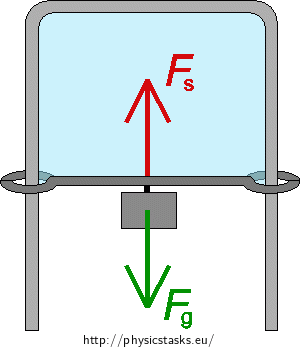
Soap Film in a Wire Frame with a Movable Crossbar
Task number: 2108
There is a soap film with the surface tension σ = 40 mN·m−1 in a wire frame with a movable crossbar of a length of 5 cm and a weight of 0.2 g.
a) What weight would keep the movable bar in equilibrium?
b) What work has to be performed to move the bar by 1.5 cm?
Analysis
Part a)
If we make a soap film in a frame with a movable crossbar, the film will strive to take up the smallest area. The film’s surface tension force will pull the bar and move it closer so that the surface of the film is smaller. As long as we want to keep the film tense, we have to pull the movable bar with adequately high force in the opposite direction and load it down with a weight.
Part b)
If we want to move the bar pulled by the tense film by a certain distance, we have to perform work. We determine the magnitude of this work as a product of the constant force with which we will pull the bar and the distance by which we move the bar.
Hint: Calculating the surface tension force
The relation for the surface tension force is
\[F_{\mathrm{s}} = σl,\]where σ is surface tension of the liquid and l is length of the edge of the surface which is pulled by the surface tension force perpendicularly to the surface of the liquid.
The soap film has two surfaces, which means that the length of the edge of this film must be counted twice. The surface tension force with which the soap film pulls the bar can be calculated from the following relation:
\[F_{\mathrm{s}} = 2σl.\]Hint to Part a)
What other force acts on the bar? What must hold true for the resultant force of the forces acting on the bar if we want it to be in equilibrium?
Hint to Part b)
With what force do we have to pull the bar, so that it is moving with a constant velocity?
Solution of Part a)
We determine the magnitude of the surface tension force with which the film is pulling the bar from the relation:
\[F_{\mathrm{s}} = 2σl.\]The bar is also pulled by its own and by the added weight. The relation which applies to the weight is
\[F_{\mathrm{g}} = mg.\]If the movable bar is to be in equilibrium, the forces acting on the bar must be in equilibrium. The surface tension force has to be equal to the weight:
\[F_{\mathrm{s}} = F_{\mathrm{g}},\]Thus, it follows that
\[2σl = mg.\tag{1}\]We want to know the mass of the weight which will hold the bar in equilibrium. We express the mass (it is the total mass of the bar and the added weight though) from relation (1):
\[m = \frac{2σl}{g}.\tag{2}\]Then, we substitute for the values known from the task assignment into relation (2) and calculate the total mass of the bar and the added weight
\[m \dot{=}\, \frac{2·40·10^{−3}·5·10^{−2}}{9.8} \mathrm{kg}\] \[m \dot{=}\, 4.1·10^{−4} \mathrm{kg}.\]The mass of the weight mw can be determined simply by subtracting the mass of the bar mb from the total mass m which we have just calculated.
\[m_{\mathrm{w}} = m −m_{\mathrm{b}}\] \[m_{\mathrm{w}} = 4.1·10^{−4} kg − 2·10^{−4} kg\] \[m_{\mathrm{w}} = 2.1·10^{−4} kg.\]Solution of Part b)
If force F of a constant magnitude acts along a trajectory of length s, it performs the work:
\[W = F·s.\]In our case the force F is determined by the magnitude of the surface tension force with which the bar is pulled by the soap film.
After substituting for the values, we get the relation:
\[W = 2σl·s.\tag{3}\]Now we substitute for the given values into relation (3) and calculate the magnitude of the work necessary to move the bar by 1.5 cm
\[W \dot{=}\, 2·40·10^{−3}·5·10^{−2}·1.5·10^{−2} \mathrm{J}\] \[W \dot{=}\, 6·10^{−5} \mathrm{J}.\]Answer
We would keep the movable bar in equilibrium by a weight of approximately 0.2 g. If we want to move the bar by 1.5 cm, we have to perform work of 60 μJ.
Link to the experiment
An experiment on this problem and on measuring the surface tension of soap water can be found here: (the link will be available soon).