Height of Water in a Capillary Tube
Task number: 2111
Two capillary tubes with the diameters of 0.1 mm and 0.3 mm are immersed by one end in a vessel of water at 20° C. How will the difference between the height of water in each capillary tube change, if we heat the water up to 70° C?
Notation
Given values:
r1 = 0.05 mm = 5·10−5 m radius of the first capillary tube r2 = 0.15 mm = 1.5·10−4 m radius of the second capillary tube Table values:
σ20 = 73·10−3 N m−1 surface tension of water at °C σ70 = 64·10−3 N m−1 surface tension of water at 70 °C ρ20 = 998.2 kg m−3 density of water at 20 °C ρ70 = 977.8 kg m−3 density of water at 70 °C Analysis
First of all, we need to think about the quantities, on which the height of water in capillary tube depends. On one hand, it depends on the diameter of the capillary tube; water will rise higher in a narrower tube. On the other hand, height of water also depends on surface tension. However, surface tension of water varies depending on temperature; when temperature increases, surface tension decreases. Density of water also depends on the temperature; after about 4 °C it also decreases, when the temperature gets higher. So, height of the water in capillary tubes will change after heating the water. Change of the diameter of the capillary tube during heating the water will not be considered.
First, we determine the height of the water in both tubes at 20 °C. After that we calculate the difference in the height of water in these capillary tubes.
Similarly, we determine the difference in the height of water in both capillary tubes at 70 °C.
Finally, we calculate the change in the difference between the height of water in each capillary tube in case of the given change of temperature.
Hint
To calculate the change of the difference between the height of water in capillary tubes, you need to know what relation for the height of liquid in a capillary tube.
The values of surface tension of water at different temperatures can be found in the Tables or on the internet.
Solution
First, we determine the difference in the height of water in the capillary tubes at 20° C.
We calculate the height of water using relation (1). Surface tension σ and density of liquid ρ depend on temperature, so we will write the temperature of the liquid in the variables' indices.
Let's denote the height of water in the capillary tube with the diameter of 0.1 mm at the temperature of 20° C by h(1)20. We determine this height from the relation
\[h^{(1)}_{20} = \frac{2σ_{20}}{r_{1}ρ_{20}g}.\tag{2}\]For the height of water in the capillary tube with the diameter of 0.3 mm at 20° C, which we have denoted by h(2)20, it applies
\[h^{(2)}_{20} = \frac{2σ_{20}}{r_{2}ρ_{20}g}.\tag{3}\]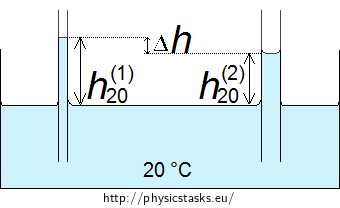
Then we calculate the difference of the height of water in the narrower capillary tube (2) and in the wider one (3)
\[Δh_{20} = h^{(1)}_{20} − h^{(2)}_{20} = \frac{2σ_{20}}{ρ_{20}g}\left(\frac{1}{r_1} − \frac{1}{r_2}\right).\tag{4}\]The analogous relation holds true to the difference of the height of water in the capillary tubes at 70° C
\[Δh_{70} = \frac{2σ_{70}}{ρ_{70}g}\left(\frac{1}{r_1} − \frac{1}{r_2}\right).\tag{5}\]Now we can determine the change in the difference of the height of water in the capillary tubes, when the temperature of water is increased from 20° C (4) to 70° C (5)
\[Δh = Δh_{20} − Δh_{70} = \frac{2}{g}\left(\frac{σ_{20}}{ρ_{20}} − \frac{σ_{70}}{ρ_{70}}\right)\left(\frac{1}{r_1} − \frac{1}{r_2}\right).\tag{6}\]Substitution for numerical values
Now we substitute for the known values into relation (6) and calculate the difference in the height of water:
\[Δh \dot{=}\, \frac{2}{9.8}\left(\frac{73·10^{−3}}{998.2} − \frac{64·10^{−3}}{977.8}\right)\left(\frac{1}{5·10^{−5}} − \frac{1}{1.5·10^{−4}}\right) m\] \[Δh \dot{=}\, 2.1·10^{−2} m. \]Answer
If the temperature changes from 20° C to 70° C, the difference between the height of water in the tubes will change by approximately 2.1 cm.
An experiment that corresponds with this task can be found here: Height of Liquid Level in Capillary Tube.




