Capillary in an Accelerating Elevator
Task number: 2222
Water rose to height h = 125 mm in a vertical glass capillary. How will the water level change if the capillary is put into a cage of a mine elevator that accelerates downward with acceleration a = 6 m·s−2?
Analysis
First let’s think through the situation where the elevator isn’t moving and the capillary with water is at rest. The resultant of all forces acting on water is equal to zero. The gravitational force acting on water in the capillary is equal to the resultant of surface forces that act on water at curved surface. (If the elevator moved with constant motion, the resultant of all forces would also be zero.)
First we will describe the situation where the elevator starts to descend with the given acceleration from the point of view of an observer that stayed outside the elevator (from the point of view of an inertial reference system). The capillary with water moves downward with even accelerated motion from his point of view. The resultant of forces acting on the water points downward. The gravitational force and the resultant of surface forces again act on the water.
The surface force depends on the radius of the capillary and the surface tension of the water - these stay the same, so the surface force stays the same as well. Water inside the capillary will have to rise higher so that the gravitational force acting on water would rise too.
We can also look at this situation from the point of view of an observer that is in the elevator (from the point of view of a non-inertial reference system). The capillary and the water inside of it are at rest relative to him. The resultant of all forces acting on water are from his point of view zero. Along with the gravitational force and the resultant of surface forces, the inertial force also acts on it pointing upward.
Hint 1 - capillary at rest or in a constant motion
Think through what forces act on water in the capillary and what their resultant is when the elevator is at rest or when it moves with constant motion. Write the relations for these forces and express the height of the water level in the capillary in this situation from them.
Hint 1 solution - capillary at rest or in constant motion
The gravitational force Fg and the resultant of surface forces Fk act on the water. The capillary with water is at rest, the resultant of acting forces has to be zero.
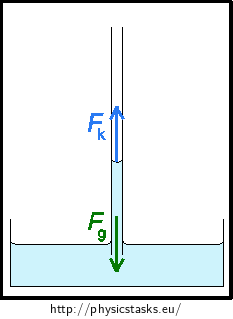
This thus applies
\[F_\mathrm{g} = F_\mathrm{k}.\tag{1}\]We can express the gravitational force as the product of mass m and gravitational acceleration g
\[F_\mathrm{g} = mg.\tag{2}\]The force Fk is given as the product of the capillary pressure pk and the area S of the inner cross section of the capillary
\[F_\mathrm{k} = p_\mathrm{k}S.\tag{3}\]If we substitute equations (2) and (3) into relation (1), we get the following equation
\[mg = p_\mathrm{k}S.\tag{4}\]We want to find the height of the surface of the water in the capillary h1. The mass of water m can be expressed as the product of density ρ and volume V of the water. The volume can be expressed as the product of the height of the water column h1 and area S
\[m = ρ·V = ρ·h_\mathrm{1}S.\tag{5}\]Substituting the equation (5) into the equation (4) gives us the following equation
\[ρh_\mathrm{1}Sg = p_\mathrm{k}S.\tag{6}\]We adjust equation (6) and we express the water level height h1 in the resting capillary
\[h_\mathrm{1} = \frac{p_\mathrm{k}}{ρg}.\tag{7}\]The capillary pressure can be calculated as
\[p_\mathrm{k} = \frac{2σ}{r},\tag{8}\]where σ is the surface tension of water and r is the radius of the capillary.
We substitute the capillary pressure from equation (8) into equation (7)
\[h_\mathrm{1} = \frac{2σ}{rρg}.\tag{9}\]Hint 2 - capillary in accelerating elevator from the point of view of an inertial observer
What forces act on the water in the capillary that is placed in an elevator that is accelerating downward with acceleration a? Where does the resultant point and what will the value of forces be in comparison with the previous situation when the elevator was at rest? How will the water level in the capillary change?
Solve this situation from the point of view of an observer that is standing outside the elevator at rest (inertial observer).
Hint 2 solution - capillary in accelerating elevator from the point of view of a non-inertial observer
The observer stands at rest outside of the elevator - an inertial observer
The gravitational force Fg acts on the water inside the capillary pointing downward and the resultant of surface forces Fk acts in the opposite direction.
The elevator and the capillary accelerate downward. A non-zero force F acts on the water:
\[F = ma,\tag{10}\]where a is acceleration with which the water and the elevator accelerate.
The resultant of surface forces that depends on the surface tension and the radius of the capillary will be of the same size as if the elevator were at rest. The gravitational force must thus increase and so the water will rise higher.
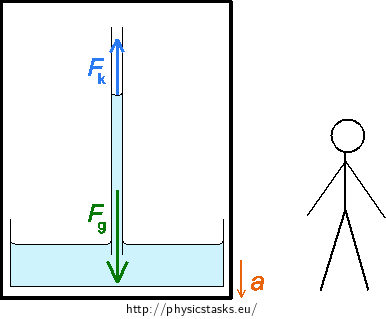
This applies for the values of forces
\[F_\mathrm{g}−F_\mathrm{k} = F.\tag{11}\]We will substitute from relations (2), (3) and (10) into the equation (11) and we will thus get the following equation
\[mg−p_\mathrm{k}S = ma\] \[m(g−a) = p_\mathrm{k}S\tag{12}\]The height of the water level h2 in the capillary can be found after some adjustments of equation (12). First we express the mass of water m as the product of density and volume of water inside the capillary
\[m = ρ·V = ρ·h_\mathrm{2}S.\]and then we will substitute this relation into equation (12). This will give us the following equation
\[ρh_\mathrm{2}S(g−a) = p_\mathrm{k}S.\tag{13}\]We will adjust relation (13), we will substitute for the capillary pressure from relation (8) and then we will express the water level height h2 in the accelerating elevator
\[ρh_\mathrm{2}(g−a) = \frac{2σ}{r}\] \[h_\mathrm{2} = \frac{2σ}{rρ(g−a)}.\tag{14}\]We will calculate the difference of water level heights Δh as the difference of water level height of an accelerating elevator h2 and water level height of a resting elevator h1 (the difference of relations (14) and (9))
\[Δh = h_\mathrm{2}−h_\mathrm{1} = \frac{2σ}{rρ(g−a)}−\frac{2σ}{rρg}.\]We will adjust this relation
\[Δh = \frac{2σa}{rρg(g−a)} \tag{15}\]and then we will simplify equation (15) using equation (9)
\[Δh = h_\mathrm{1}\frac{a}{g−a}.\tag{16}\]Hint 3 - capillary in accelerating elevator from the point of view of non-inertial observer
We can also solve the situation from the point of view of an observer standing in the elevator (non-inertial observer).
Think through how the capillary moves, what forces act on the water inside the capillary and what their resultant is relative to the observer.
Hint 3 solution - capillary in accelerating elevator from the point of view of non-inertial observer
The observer stands inside the elevator - non-inertial observer
The water in the capillary is at rest relative to the observer in the elevator, the resultant of forces acting on the water must be zero. The gravitational force Fg and the resultant of surface forces Fk act on the water just like in the second part. Now, however, the inertial force Fs acts on it as well. This force exists only in non-inertial systems.
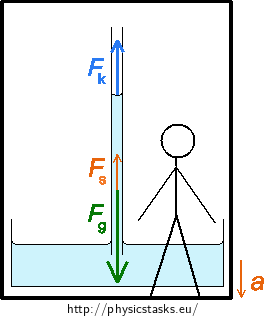
This applies for the resultant of forces
\[\vec{F_\mathrm{g}}+\vec{F_\mathrm{k}}+\vec{F_\mathrm{s}} = 0.\]The gravitational force points downward, the resultant of surface forces Fk and the inertial force Fs point upward. This applies for the sizes of these forces
\[F_\mathrm{g}−F_\mathrm{k}−ma = 0.\]We will substitute for forces Fg and Fk from relations (2) and (3)
\[mg−p_\mathrm{k}S−ma = 0.\]We will adjust this relation
\[m(g−a) = p_\mathrm{k}S.\tag{12}\]We get the same relation (12) like we did in the previous section where we solved the situation from the point of view of an inertial observer. We would then solve the task the same way and we would get the same relation (16) for the water level height difference
\[Δh = h_\mathrm{1}\frac{a}{g−a}.\tag{16}\]Whether we observe the capillary from inside the moving elevator or from outside the moving elevator, we will see that the water level rises by the same amount Δh as the capillary moves downward.
Numeric substitution
The difference of water level heights Δh between the capillary at rest and the accelerating capillary can be determined from relation (16)
\[Δh = h_\mathrm{1}\frac{a}{g−a}.\tag{16}\]We will substitute the given values and calculate
\[Δh = 1.25·10^{−1}·\frac{6}{10−6} \mathrm{m}\] \[Δh \dot{=}\, 187.5·10^{−3} \mathrm{m} \dot{=}\, 187.5 \mathrm{mm}.\]Answer
The water level height in an accelerating elevator with downward acceleration of 6 m·s−1 will be 187.5 mm higher than in a resting elevator.




