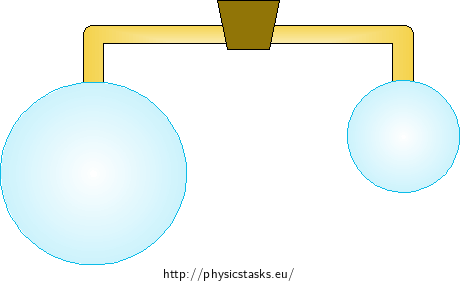
Two connected soap bubbles
Task number: 2077
We blow two soap bubbles of different diameters \(r < R\) on the opposite ends of a glass tube that has a valve on it. What happens to the bubbles when we open the valve (we let the air flow from one bubble into the other)? Will the diameters of the bublles change in any way?
Analysis
The expected change of the diameters of the bubbles depends on the pressures of air inside the bubbles. If there is a higher pressure in one of the bubbless, the air will flow from it into the other bubble.
The pressure inside the bubble is given by the atmospherical pressure, the equlibrium pressure of the water vapor evaporated from the surfaces of the bubbles and by the Laplace pressure of the soapy-water bubble membrane on its insides.
The atmospherical pressure and the vapor pressure inside both bubbles is the same. The pressure of the spherical bubble membrane is called the Laplace pressure and it depends on the radius of the membrane surface.
We derive the dependence of the Laplace pressure on the bubble radius by considering a small decrease of the bubble radius, accompanied with a decrease of the volume and the surface area of the bubble membrane. We express the work of the surface forces of the bubble membrane as:
- the change of the surface energy of the membrane upon the decrease of bubble surface area,
- the work done by the Laplace pressure of the membrane upon the decrease of the bubble volume.
1st part of solution - Calculation of Laplace pressure
When the bubble shrinks its diameter by Δr, its volume decreases by ΔV, and its surface area decreases by ΔS.
The work of the surface forces done against the air inside the bubble is simply given by the Laplace pressure of the bubble membrane and the change of the volume of the air:
\[ΔW = {p_{\mathrm{L}}ΔV},\]The corresponding change of the surface area of the bubble membrane is accompanied with a change of the surface energy E of the bubble membrane. Its change is:
\[ΔE = {σΔS},\]where σ is the surface tension of the liquid that forms the membrane and ΔS is the change of the membrane surface area.
The work done by the surface forces of the membrane is equal to the change of the surface energy of the membrane:
\[\Delta W = \Delta E \\ p_\mathrm{L}\Delta V = \sigma \Delta S.\]We factor out the Laplace pressure:
\[p_\mathrm{L} = \frac{\sigma \Delta S}{\Delta V}.\tag{1}\]2nd part of solution - Expressing ΔV and ΔS
First, we derive the dependence of the change of the bubble volume on a tiny change of its radius. The volume of the spherical bubble with radius r is:
\[V = \frac{4}{3}πr^{3}\]When the radius of the bubble increases by Δr, its volume increases by ΔV. We calculate the change of the volume as the difference between the volumes of the increased bubble (having the increased radius \(r + \Delta r\)) and of the original bubble with radius r:
\[ΔV = \frac{4}{3}π(r+Δr)^{3} - \frac{4}{3}πr^{3}\]We express the third power:
\[ΔV = \frac{4}{3}π(3r^{2}Δr + 3rΔr^{2} + Δr^{3}).\]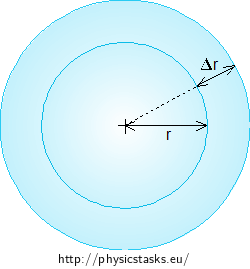
Let us consider that the change of the bubble radius Δr is a very small number compared to the original radius r. The products 3rΔr2 and Δr3 are thus much smaller numbers than 3r2Δr and we can neglect them in the summation with respect to 3r2Δr. We thus get a simpler formula for the change of the bubble volume:
\[ΔV = 4πr^{2}Δr.\tag{2}\]Second, we determine the dependence of the surface area of the bubble membrane on a tiny change of its radius. The membrane of the bubble is made of a very thin layer of soapy water. The membrane has two surfaces - the outer one and the inner one. The radii of the two surfaces are practically the same, owing to the thinness of the membrane.
The total surface area of the bubble membrane is then twice the surface area of a sphere of radius r:
\[ΔS = 2·4πr^{2}.\]When the radius of the bubble changes by Δr, we obtain the change of the surface area of the membrane ΔS as the difference between the surface areas of the membrane of the increased bubble with radius \(r + \Delta r\) and of the original bubble with radius r:
\[ΔS = 8π(r+Δr)^{2} - 8πr^{2}.\]We express the second power:
\[ΔS = 8π(2rΔr + Δr^{2}).\]Since the radius change Δr is much smaller than the radius r, we can neglect the term Δr2 in the summation with respect to the term 2rΔr and we get the simplified formula for the change of the surface area of the bubble membrane:
\[ΔS = 16πrΔr.\tag{3}\]Comment - Expressing ΔS and ΔV using differential calculus
We can express the change of the bubble volume and the surface area of the bubble membrane upon small change of its radius also as differentials.
We differentiate the volume V of the sphere with respect to its radius r:
\[\frac{dV}{dr} = \frac{d}{dr} \left( \frac{4}{3} \pi r^3 \right) = \frac{4}{3}\pi \cdot 3 r^2\] \[dV = 4 \pi r^2 \, dr.\]We find the change of the surface area of the membrane the same way. Remember that the membrane has two surfaces:
\[\frac{dS}{dr} = 2 \frac{d}{dr}(4 \pi r^2) = 8 \pi \cdot 2 r\] \[dS = 16 \pi r \, dr.\]We can see that the differentials of volume and surface area are equivalent to formulae (2) and (3). It follows that this differential approach would yield the same result.
3rd part of solution - Expressing Laplace pressure
What happens after interconnecting the bubbles?
We connect two bubbles of different diameters in thist task. The formula (4) dictates that the Laplace pressure is inversely proportional to the radius of the bubble. This means that the surface forces produce a larger pressure in the smaller bubble than in the larger one. After connecting the insides of the bubbles, the air will start to flow from the smaller one to the bigger one. The bigger bubble will grow and the smaller one will shrink to a flat membrane at the end of the connecting tube.
Note: Find an experiment with a movie to this task here: Two soap bubbles connected with a tube.





