Capillary action between glass plates
Task number: 2076
Two glass plates are partially dipped in water in vertical position, touching at one of their vertical edges and forming a very small angle ε between them. Assess the height h of the surface of the liquid between the glass plates as a function of the horizontal distance x from the touching edge.
Hint
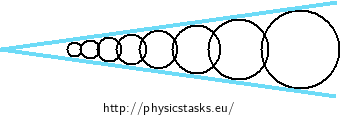
Start from the phenomenon of capillary action of a liquid in a cylindrical tube. Think of the wedge-shaped space between the glass plates as if it was filled with a series of vertical tubes whose diameter inreases from the edge of the angle (see the Figure below). Express the distance between the glass plates (the diameter of the imaginary capillary tubes) as a function of the distance from the edge of the angle. Apply the relation between the height of a liquid column in a tube and the diameter of the tube.
Theory - Surface tension
Molecules in a liquid attract each other by the so called cohesive forces. These forces act notably on short distances and decrease rapidly with increasing distance from the molecule. In the bulk of the liquid, each molecule is pulled equally in all directions by the neighbouring molecules and there is a zero net force on the molecule.
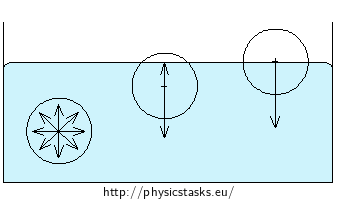
Molecules near the surface of the liquid do not have as many upper neighbors as the lower neighbors. The net attraction to the lower neighboring molecules pulls the surface molecules inwards to the liquid, perpendiculary to the surface. The force decreases with the distance from the surface - the molecules arrange so that the least number of them liest at the very surface layer. Consequently, the liquid as a whole takes such shape, that its surface is the least in given environment – a falling piece of water takes the shape of a spherical drop.
The surface molecules are also attracted outwards by the molecules of the gas above the liquid surface. However, the effect of these forces is usually negligible due to the substantially lower concentration of molecules in the gas than in the liquid.
Altogether, the surface of a liquid behaves like a stretched elastic membrane and small objects such as needles or lightweight coins can float on the elastic surface of the liquid. The quantity that describes the strength of the liquid surface is called the surface tension.
Theory - Capillary action
Capillary action occurs on a liquid when it meets narrow solid spaces, such as slits or thin tubes (called capillary tubes). Capilary action pushes the liquid up in the tube when the liquid wets the material of the tube (such as water in glass), or down when the liquid does not wet the tube (such as mercury in glass). A liquid wets a solid material when the attraction between the molecules of the liquid and the solid material (adhesion) is stronger then the attraction among the molecules of the liquid (cohesion). A non-wetting liquid has a higher internal cohesion than is its adhesion to the given solid material.
Capillary action in capillar tubes is a consequence of surface tension of the liquid surface and of the wetting of the tube wall with the liquid. The wetting liquid is drawn up a little bit by its adhesion to the wall of the tube. The surface of the liquid thus becomes concave (hollow). The surface tension on the curved surface of the liquid gives rise to an additional pressure, called the Laplace pressure. The Laplace pressure acts always towards the center of curvature of the curved surface, which is upwards in the case of the concave surface of the wetting liquid.
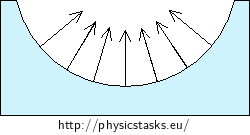
A non-wetting liquid is more strongly drawn together than to the wall of the tube - the liquid dewetts the wall of the tube and forms a convex (domed) surface in the tube. The Laplace pressure acts downwards in this case.
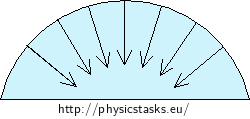
The water rises by capillary action to different heights in glass tubes of different diameters - the thinner tube, the higher the water rises.
Solution part 1 - Height of capillary action in a cylindrical tube
We derive the height of the water column held by capillary action in thin tubes, when the curved surface in the tube takes the shape of a half-sphere with a radius equal to the radius of the tube. The capillary action can be also derived for wider tubes, when the surface of the liquid is notably curved only near the tube wall.
The Laplace pressure of a curved surface with radius R is
\[p_L = \frac{2σ}{R}.\]Note: The formula for Laplace pressure of a curved surface is derived for a membrane with two surfaces in the task Two connected soap bubbles.
The Laplace pressure draws water up in the tube to the height h at which it is equaled by the hydrostatic pressure pS of the water column risen above the surrounding water level. The hydrostatic pressure of the water column is:
\[p_S = h \rho g,\]where ρ is the density of water and g is the gravitational acceleration. The two pressures are equal when water does not further rise or drop:
\[\frac{2 \sigma}{R} = h \rho g\]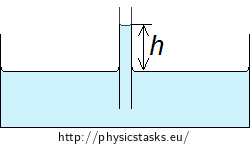
And the height of the water column is
\[h = \frac{2σ}{Rρg}.\tag{1}\]We can see that the height of the water column is inversely proportional to the diameter of the tube.
Note: Capillary action in non-wetting liquids
The surface of a non-wetting liquid (e.g. mercury in glass) is decreased in the tube by the height h.
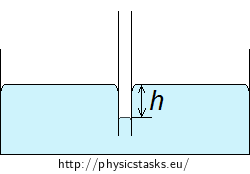
The Laplace pressure presses the liquid down in the tube to the depth h at which it is equaled by the hydrostatic pressure pS of the surrounding liquid. The hydrostatic pressure of the liquid at depth h below the free surface is:
\[p_S = h \rho g,\]where ρ is the density of the liquid and g is the gravitational acceleration. The two pressures are equal when the liquid does not further rise or drop:
\[\frac{2 \sigma}{R} = h \rho g\]And the height of the liquid column is
\[h = \frac{2σ}{Rρg}.\]The formula for the depth of the non-wetting liquid column is the same as the formula for the height of the wetting liquid column.
Solution part 2 - dependence of capillary radius on the distance from the edge angel
The surface of water between the two sheets of glass that form the small angle ε will rise the highest at the edge of the angle where the imaginary capillary tube has the smallest diameter. The height of the water surface will decrease with increasing distance from the angle edge.
We assess the height of water at the axis of the angle, where the curved surface has its minimum when seen from the side. The height of water at point C at a distance x from the angle edge is given by the distance to the nearest point of the glass sheets, i.e. by the diameter R of the imaginary circular tube as drawn in the Figure below.
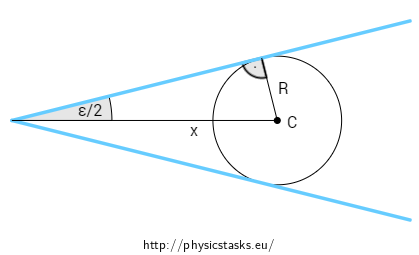
The radius of the imaginary cylindrical tube is:
\[R = x \sin{\frac{\varepsilon}{2}}.\tag{2}\]The height of the surface
Answer
The height of the water surface depends on the distance x from the angle wedge as:
\[h = \frac{1}{x} \frac{2σ}{ρgsin\frac{ε}{2}}.\]All the quantities in the right hand fraction are constants. The surface of water in the wedge will thus take the shape of a hyperbola \(h \propto 1/x\).
Link to experiment
An experiment for this task can be found here: Capillary action between two glass plates.




