Bimetal
Task number: 2110
Copper and zinc strips have the same length of 20 cm at a temperature of 20 °C.
a) What will be the difference in length of the strips at a temperature of 100 °C?
b) The strips were rivetted together at 20 °C and formed a so-called bimetallic strip. Assume that it bends into an arc when heated. Determine which metal will be on the outer side of the arc and what will be the radius of the arc at 100 °C. Thickness of each strip is 1 mm.

Notation
t0 = 20 °C temperature at which both strips are equally long l0 = 20 cm = 0.20 m length of both strips at temperature t0 t = 100 °C temperature to which the strips are heated Δl = ? difference in the length of both strips at temperature t d = 1 mm = 1·10−3 m thickness of each strip r = ? radius of the bent bimetallic strip From the Tables αZn = 30·10−6K−1 coefficient of linear thermal expansion of zinc αCu = 17·10−6K−1 coefficient of linear thermal expansion of copper Analysis
Substances expand when we increase their temperature. Different substances expand differently, that is why there will be the difference in the length of the two strips. As long as the strips are firmly rivetted together so that they cannot move along each other, they will bend. The strip which expands less will be on the inner side, so in our case it will be copper. Since the thickness of the strips is constant, two curves differ in their length. The difference in the length of both arcs then must correspond to the difference in length caused by the different thermal expansion of the two metals.
Solution of a)
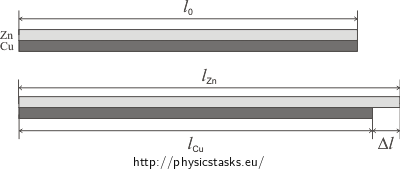
First, we express the length of both strips at temperature t.
\[l_{Cu}=l_0\,(1+\alpha_{Cu}\Delta t)\] \[l_{Zn}=l_0\,(1+\alpha_{Zn}\Delta t)\]We subtract one length from another:
\[\Delta l=l_{Zn}-l_{Cu}\] \[\Delta l=l_0\,(1+\alpha_{Zn}\Delta t)-l_0\,(1+\alpha_{Cu}\Delta t)\] \[\Delta l=l_0\,(\alpha_{Zn}-\alpha_{Cu})\Delta t\] \[\Delta l=l_0\,(\alpha_{Zn}-\alpha_{Cu})\,\left(t-t_0\right)\]Finally, we substitute for numerical values:
\[\Delta l=l_0\,(\alpha_{Zn}-\alpha_{Cu})\,\left(t-t_0\right)\] \[\Delta l=0.2\cdot\,(30\cdot{10^{-6}}-17\cdot{10^{-6}})\cdot\,\left(100-20\right)\,\mathrm{m}\] \[\Delta l=2.08\cdot{10^{-4}}\,\mathrm{m}=0.208\,\mathrm{mm}\]Hint on b): How to determine the radius of the bimetallic strip?
Since the strips are firmly attached to each other, they will bend during heating. Consider that the length of the strip corresponding to the increased temperature is in the middle of the strip.
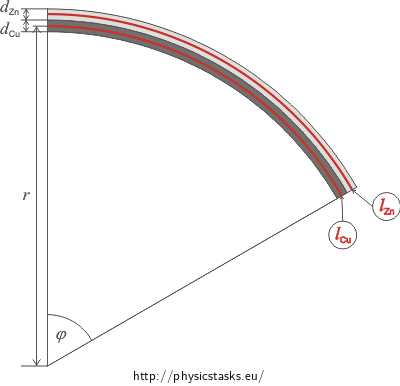
We have already expressed the length of both strips in part a), but we can also express it through angle φ and the desired radius r. Therefrom we can determine the radius r.
Note: When the temperature increases, the thickness of the strips also increases. However, this effect has very little impact on the result, therefore you may ignore it.
Solution of b)
We will use the picture to calculate the radius of the arc. Since the strips are firmly attached to each other, they will bend during heating. Consider that the length of the strip corresponding to the increased temperature is in the middle of the strip.

Denote the radius of the smaller arc by r. Radius of the larger arc will be R:
\[R=r+\frac{d_1+d_2}{2}\]where d1 and d2 are the “magnified” thicknesses of both strips. The length of the circular arc can be determined as a product of the radius and angle φ (in radians).
\[l_{Cu}=r\varphi\] \[l_{Zn}=(r+\frac{d_{Zn}}{2}+\frac{d_{Cu}}{2})\varphi\]We subtract the length of one arc from the other one and realize that their difference must equal the difference in the length of the strips that we expressed in part a) of this task.
\[\Delta l=l_{Zn}-l_{Cu}=(r+\frac{d_{Zn}}{2}+\frac{d_{Cu}}{2})\varphi-r\varphi=\frac{1}{2}(d_{Zn}+d_{Cu})\varphi\]We substitute the difference in lengths and the “magnified” thicknesses at the increased temperature
\[l_0\,(\alpha_{Zn}-\alpha_{Cu})\Delta t=\frac{1}{2}[d(1+\alpha_{Cu}\Delta t)+d(1+\alpha_{Zn}\Delta t)]\varphi \] \[l_0\,(\alpha_{Zn}-\alpha_{Cu})\Delta t=\frac{1}{2}d[2+(\alpha_{Cu}+\alpha_{Zn})\Delta t)]\varphi \]From this equation we can express the unknown angle:
\[\varphi=\frac{2l_o(\alpha_{Zn}-\alpha_{Cu})\Delta t}{d[2+(\alpha_{Cu}+\alpha_{Zn})\Delta t)]}\]For the length of the heated copper strip it holds true
\[l_o(1+\alpha_{Cu}\Delta t)=r\varphi\]Therefrom we express the desired radius r and substitute the angle φ for its expression:
\[r=\frac{l_o(1+\alpha_{Cu}\Delta t)}{\varphi}=\frac{l_o(1+\alpha_{Cu}\Delta t)}{\frac{2l_o(\alpha_{Zn}-\alpha_{Cu})\Delta t}{d[2+(\alpha_{Cu}+\alpha_{Zn})\Delta t)]}}\] \[r=\frac{(1+\alpha_{Cu}\Delta t)[2+(\alpha_{Cu}+\alpha_{Zn})\Delta t]}{2(\alpha_{Zn}-\alpha_{Cu})\Delta t}\,d\]Finally, we substitute for given values:
\[r=\frac{(1+17\cdot{10^{-6}}\cdot{80})[2+(30\cdot{10^{-6}}+17\cdot{10^{-6}})\cdot80]}{2\cdot(30\cdot{10^{-6}}-17\cdot{10^{-6}})\cdot80}\cdot{10^{-3}}\,\mathrm{m}\] \[r\,\dot{=}\,0.9647\,\mathrm{m}\,\dot{=}\,96\,\mathrm{cm}\]Note: If we look more closely at both expressions in brackets in the numerator of the resultant fraction, it is obvious that we can omit the terms which contain the thermal coefficients αZn and αCu. The first expression in brackets is related to the change in length of one strip and the second expression in brackets corresponds to the change in the strip’s thickness. On the contrary, we cannot do any omission of the expression in brackets in the denominator, because both terms are of a similar magnitude. This expression is related to the difference in the linear extension of both metals. This will give us a simpler relation:
\[r\,\dot{=}\,\frac{(1+...)[2+...]}{2(\alpha_{Zn}-\alpha_{Cu})\Delta t}\,d=\frac{d}{(\alpha_{Zn}-\alpha_{Cu})\Delta t}\] \[r\,\dot{=}\,\frac{10^{-3}}{(30\cdot{10^{-6}}-17\cdot{10^{-6}})\cdot{80}}\,\mathrm{m}\,\dot{=}\,0.9615\,\mathrm{m}\,\dot{=}\,96\,\mathrm{cm}\]Answer
The difference in the length of the two strips will be about 0.2 mm, and the bimetallic strip will bend into the arc with the radius of approximately 96 cm.




