Capillary with a Sealed End

Task number: 2221

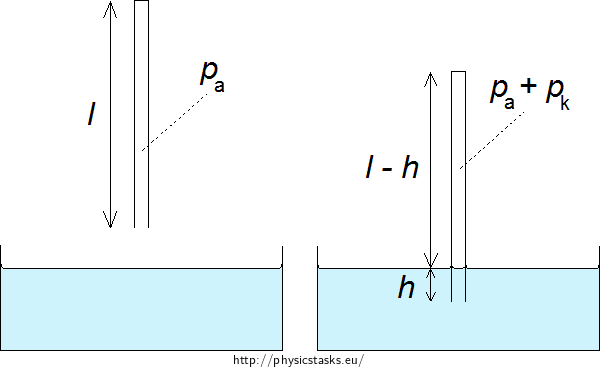
A glass capillary with inner diameter of d = 0.2 mm and length l = 20 cm is sealed at one end. The other end is submerged in water in a way that the water surface inside and outside are in the same height. The capillary’s end is h = 2.9 mm deep. How big is the surface tension of water against air?

List of Known Information

r = 0.1 mm = 10⁻⁴ m	capillary’s inner diameter
l = 20 cm = 2·10⁻¹ m	length of the capillary
h = 2.9 mm = 2.9·10⁻³ m	length of submerged part of the capillary
p_a = 10⁵ Pa	atmospheric pressure
σ = ?	water’s surface tension

Analysis
First think through what happens to the air inside the capillary when we submerge it in water. The air fills the capillary and has atmospheric pressure in the beginning. After submersion water gets inside the capillary and the volume of the air decreases which causes a rise in its pressure. This rise is the same as the capillary pressure.

We can consider air to be ideal gas at normal conditions. During the submersion the temperature of the air will not change. We can write the equation of state for isothermal process for the air before and after the submersion. We will then express pressure from the equation. The capillary pressure can also be expressed using the radius of the capillary and the wanted surface tension of water.
Hint 1 - pressure and volume of air inside the capillary
Think through what the volume and pressure of air inside the capillary before and after the submersion is.
Hint 1 solution - pressure and volume of air inside the capillary
The volume of air inside the capillary before submersion is V₁. This volume can be expressed as
\[V_\mathrm{1} = πr^{2}l,\tag{1}\]
where r is the diameter of the capillary and l is the length of the inner side of the capillary.

The air pressure inside the capillary is the same as the air pressure outside the capillary. It is the atmospheric pressure p_a.

The water will rise to height h after the submersion. The volume of air inside the capillary can then be calculated as
\[V_\mathrm{2} = πr^{2}(l−h).\tag{2}\]
The air pressure inside the capillary will increase by the capillary water pressure as the water pushes the air inside the capillary. The total pressure in the capillary will then be
\[p_\mathrm{2} = p_\mathrm{a} + p_\mathrm{k}.\tag{3}\]
Hint 2 - equation of state
The air inside the capillary can be considered an ideal gas at normal conditions. Write the equation of state for air inside the capillary before and after submersion. What process can we consider the air compression to be?
Hint 2 solution - equation of state
We can consider the air compression inside the capillary as isothermal process. The equation of state for isothermal process is formulated as
\[p_\mathrm{1}V_\mathrm{1} = p_\mathrm{2}V_\mathrm{2}.\tag{4}\]
If we substitute the pressure and volume from relations (1), (2) and (3) into the equation of state (4), we get equation
\[p_\mathrm{a}πr^{2}l = (p_\mathrm{a}+p_\mathrm{k})πr^{2}(l−h).\tag{5}\]
Hint 3 - relation for capillary pressure calculation
Recall the relation for capillary pressure calculation. The capillary pressure can also be expressed from the equation of state. We will then determine the water surface tension from these two equations.
Hint 3 solution - relation for capillary pressure calculation
This equation applies for capillary pressure p_k
\[p_\mathrm{k} = \frac{2σ}{r},\tag{6}\]
where σ is the surface tension of a liquid and r is the radius of the capillary.
Complete Solution
The pressure inside the capillary is the atmospheric pressure p_a before we submerge the capillary into water.

The volume of the capillary V₁ can be calculated as
\[V_\mathrm{1} = πr^{2}l,\tag{1}\]
where r is the diameter of the capillary and l is the length of the inner side of the capillary.

The product of the pressure and the air volume inside the capillary before submersion is
\[p_\mathrm{1}V_\mathrm{1} = p_\mathrm{a}πr^{2}l.\]
The volume of air will decrease to V₂ after the submersion of the capillary into the water
\[V_\mathrm{2} = πr^{2}(l−h),\tag{2}\]
where h is the height of water inside the capillary.

The air pressure inside the capillary will also increase by the capillary water pressure p_k. The pressure in the capillary will then be p₂
\[p_\mathrm{2} = p_\mathrm{a} + p_\mathrm{k}.\tag{3}\]
After the submersion, the product of the pressure and the air volume in the capillary will be equal to
\[p_\mathrm{2}V_\mathrm{2} = πr^{2}(p_\mathrm{a} + p_\mathrm{k})(l−h).\]
According to the equation of state for isothermal process, this applies
\[p_\mathrm{1}V_\mathrm{1} = p_\mathrm{2}V_\mathrm{2}\tag{4}\]
after substitution from equations (1), (2) and (3) into the equation of state, we receive
\[p_\mathrm{a}πr^{2}l = πr^{2}(p_\mathrm{a} + p_\mathrm{k})(l−h).\tag{5}\]
We will adjust the relation and we will express the capillary pressure
\[p_\mathrm{k} = \frac{p_\mathrm{a}h}{l−h}\]
We want to know the value of the surface tension of water. We can calculate the surface tension σ using the value of the capillary pressure and relation
\[p_\mathrm{k} = \frac{2σ}{r}.\tag{6}\]
Substituting the relation (6) into adjusted relation (5) will yield us relation for calculation of the surface tension of water
\[σ = \frac{p_\mathrm{a}rh}{2(l−h)}.\tag{7}\]
Numeric Substitution
The value of surface tension of water can be calculated from relation (7)
\[σ = \frac{p_\mathrm{a}rh}{2(l−h)}.\]
After substitution of numeric values from assignment, we receive equation
\[σ = \frac{10^{5}·10^{−4}·2.9·10^{−3}}{2·(2·10^{−1}−2{,}9·10^{−3})} N·m^{−1}\] \[σ \dot{=}\, 74·10^{−3} N·m^{−1}.\]
Answer
The surface tension of water is approximately 74·10⁻³ N·m⁻¹.
Comment
The surface tension of water is dependent on the water’s temperature. The higher the temperature the lower the surface tension. We have calculated that the water has surface tension of σ = 74·10⁻³ N·m⁻¹ which corresponds to temperature of 11 °C.

The table of surface tension temperature dependence was found at Converter (Czech website).