Collection of Solved Problems in Physics

The Most Probable, Average and Root-Mean-Square Speed of Gas Molecules

Task number: 2174

• Hint: Maxwell-Boltzmann Distribution

  Maxwell-Boltzmann distribution describes a classical system of distinguishable particles, such as for example molecules. A distribution function for the magnitude of velocity of the molecules is defined as follows

  \[\rho \left( v\right) = 4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}}v^{2}e^{-\frac{mv^{2}}{2kT}}.\]

• Analysis

  The most probable speed of gas molecules described by the Maxwell-Boltzmann distribution is the speed at which distribution graph reaches its maximum. Thus, if we know the formula of this distribution, we just need to differentiate it and consider the derivative to be equal to zero. Speed for which the derivate equals zero is the most probable speed.

  The average speed of molecules is the mean of all magnitudes of velocity at which molecules of the given gas are moving.

  The root-mean-square speed of molecules is the speed at which all the molecules have the same total kinetic energy as in case of their actual speed.

  The average speed of molecules can be calculated as an integral of the Maxwell-Boltzmann distribution function multiplied by the magnitude of velocity of a molecule v. The variable of integration, velocity, can attain all possible values, therefore we integrate from zero to infinity.

  The root-mean-square speed can be calculated in a similar way, the only difference is that we multiply the Maxwell-Boltzmann distribution function by v².

• Solution

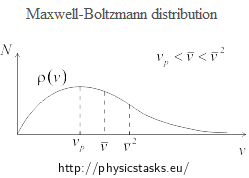
  The following figure shows the Maxwell-Boltzmann distribution of the magnitude of velocity of gas molecules.

  In the figure, the most probable speed v_p, average speed \(\bar{v}\) and root-mean-square speed \(\bar{v}^{2}\) are marked.

   

  

  The most probable speed corresponds to the maximum of distribution function (see figure). First, we write this distribution function

  \[\rho \left( v\right) = 4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}}\,v^{2}\,e^{-\frac{mv^{2}}{2kT}},\]

  where m is the mass of one molecule, k is the Boltzmann constant and T stands for thermodynamic temperature.

  Then we differentiate the distribution function with respect to the magnitude of velocity v and consider the obtained derivative to be equal to zero (this is a general procedure for finding extremes of function).

  We obtain:

  \[\frac{\mathrm{d}\rho \left( v\right) }{\mathrm{d}v} = 4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}} \left( 2v\,e^{-\frac{mv^{2}}{2kT}} + v^{2}\,\left( -\frac{mv}{kT}\right) e^{-\frac{mv^{2}}{2kT}}\right) =\] \[=4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}}e^{-\frac{mv^{2}}{2kT}}\ v\ \left( 2 - \frac{m}{kT}v^{2}\right) = 0\]

  During differentiation we have used the product rule and the chain rule. Then we make use of the fact that neither the factored-out constants nor the value of the exponential function can be equal to zero. Thus, we have two possible solutions

  \[ v = 0\qquad \mathrm{or} \qquad 2-\frac{m}{kT}v^{2} = 0.\]

  The first option, speed equals zero, corresponds to the minimum of the distribution function. From the second option, we get:

  \[v^{2} = \frac{2kT}{m},\] \[v = \sqrt{\frac{2kT}{m}}.\]

  For further adjustment, we use the relation for the gas constant R = kN_A (where N_A stands for the Avogadro constant) and for the molar mass of gas M_m = mN_A. We obtain

  \[v_{p} = \sqrt{\frac{2kT}{m}} = \sqrt{\frac{2RT}{M_{m}}}.\]

   

  Then we calculate the average speed of gas molecules. For this speed it holds true

  \[\bar{v} = \int_0^{\infty}{v \rho(v)}\,\mathrm{d}v = \int_0^{\infty}{4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}}v^{3}e^{-\frac{mv^{2}}{2kT}}}\,\mathrm{d}v.\]

  To make the calculation more transparent, we introduce the following notation:

  \[a = 4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}}\] \[b = \frac{m}{2kT}\]

  Thus, we obtain:

  \[\bar{v} = a\int_0^{\infty}{v^{3}e^{-bv^{2}}}\,\mathrm{d}v\]

  Now we use the substitution s = v², ds = 2vdv and get:

  \[\bar{v} = \frac{a}{2}\int_0^{\infty}{se^{-bs}}\,\mathrm{d}s\]

  After that we apply partial integration (differentiate s and integrate e^−bs. We obtain:

  \[\bar{v} = \frac{a}{2}\cdot \left( \left[ -s\frac{1}{b}e^{-bs}\right] _{0}^{\infty} - \int_0^{\infty}{-\frac{1}{b}e^{-bs}}\,\mathrm{d}s \right) = \frac{a}{2}\,\left( 0+\frac{1}{b}\int_0^{\infty}{e^{-bs}}\,\mathrm{d}s\right) =\] \[=\frac{a}{2b}\left[-\frac{1}{b}e^{-bs}\right] _{0}^{\infty} = \frac{a}{2b^{2}} \]

  Finally, we substitute a and b and get:

  \[\bar{v} = \frac{4\pi}{2}\sqrt{\left( \frac{m}{2\pi kT}\right) ^{3}}\cdot \frac{4k^{2}T^{2}}{m^{2}} = \sqrt{\frac{8kT}{\pi m}} =\sqrt{\frac{8RT}{\pi M_{m}}}.\]

   

  Now let’s calculate the root-mean-square speed. We will need to use the following formula, which can be found in the Table of Integrals.

  \[\int_{0}^{\infty}{x^{2n}e^{-\frac{x^{2}}{a^{2}}}}\, \mathrm{d}x = \sqrt{\pi}\,\frac{\left( 2n\right) !}{n!}\,\left( \frac{a}{2}\right) ^{2n+1}\]

  For the root-mean-square speed it applies:

  \[\bar{v}_{k}^{2} = \int_{0}^{\infty}{v^{2}\rho\left( v\right) }\, \mathrm{d}v = 4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}} \int_0^{\infty}{v^{4}e^{-\frac{mv^{2}}{2kT}}}\,\mathrm{d}v = \] \[=4\pi \left( \frac{m}{2\pi kT}\right) ^{\frac{3}{2}}\ \sqrt{\pi}\,\frac{4!}{2!}\,\left( \frac{\sqrt{\frac{2kT}{m}}}{2}\right) ^{5} = \frac{3}{2}\sqrt{\left( \frac{m}{2\pi kT}\right) ^{3}\pi ^{3}\left( \frac{2kT}{m}\right) ^{5}}=\] \[=\frac{3kT}{m} = \frac{3RT}{M_{m}}\]

  Then the magnitude of the root-mean-square velocity is

  \[\bar{v}_{k} = \sqrt{\frac{3RT}{M_{m}}}.\]

• Answer

  The magnitude of the most probable velocity of molecules of the gas described by Maxwell-Boltzmann distribution is given by the relation

  \[v_{p} = \sqrt{\frac{2kT}{m}} = \sqrt{\frac{2RT}{M_{m}}}.\]

  The average speed can be determined from \[\bar{v} = \sqrt{\frac{8RT}{\pi M_{m}}}\] and for the magnitude of the root-mean-square velocity it holds true \[\bar{v}_{k} = \sqrt{\frac{3RT}{M_{m}}}\,.\]