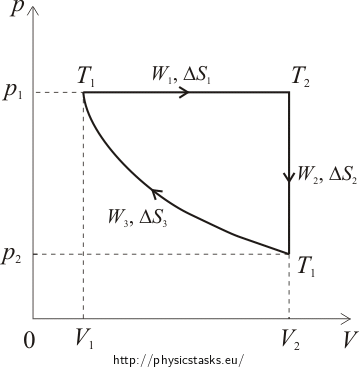
Cyclical Reversible Process
Task number: 3941
Determine total work, entropy change and efficiency of a reversible process consisting of isobaric expansion, isochoric cooling and isothermal compression. Compare the efficiency of this cycle with the efficiency of ideal Carnot cycle, provided that both cycles work between temperatures 300 K and 1000 K.
Assume the two-atom ideal gas with amount of substance of 1 mol.
Given Values
T1 = 300 K temperature of first bath T2 = 1000 K temperature of second bath n = 1 mol amount of substance of gas W = ? total work ΔS = ? entropy change η = ? efficiency ηid = ? efficiency of ideal Carnot cycle Table values:
R = 8.31 JK−1mol−1 molar gas constant Hint 1 – Total Work
Total work W is equal to the sum of work done by the gas in individual parts of the cycle.
How do you determine these values of work?
Hint 2
To express unknown volumes V1, V2 and pressures p1, p2 use the equation of state for ideal gas.
Analysis – Total Work
During the determination of total work we must consider when the work is performed by the gas and when it is performed by the surroundings.
During isobaric expansion, the work performed by the gas is determined as a product of pressure and volume change. During isochoric process the gas volume does not change and the performed work is zero. During isothermal compression the work is performed by the surroundings. Since during this process the pressure is not constant, we need to use integral calculus to determine the performed work.
To express pressure as a volume function we use Boyle's Law.
Solution – Total Work
When determining the total work W we must consider when the work is performed by the gas and when it is performed by the surroundings.
During isobaric expansion the gas increases its volume and performs work W1. This can be determined as
\[W_1=p_1\left(V_2-V_1\right),\]where p1 is the gas pressure and V1 and V2 its volume before and after expansion.
During isochoric process the volume of gas does not change and the system therefore does not perform work
\[W_2=0.\]During isothermal compression the gas is being compressed. The work W3 performed by the gas is therefore negative (it is performed by the surroundings). Since during isothermal process the pressure p is not constant, we need to use integral calculus to determine the work:
\[W_3 = \int\limits_{V_2}^{V_1}p\, \text{d}V,\]where V2 is the volume of the gas before compression and V1 its volume after compression.
Pressure p as a function of volume V can be expressed from Boyle's Law:
\[p_2V_2 = pV. \]We obtain
\[p = \frac{p_2V_2}{V}\]and now we can continue to the integration
\[W_3 = \int\limits_{V_2}^{V_1}p\, \text{d}V = \int\limits_{V_2}^{V_1}\frac{p_2V_2}{V}\, \text{d}V =\]We factor the constants out of the integral
\[=p_2V_2 \int\limits_{V_2}^{V_1}\frac{1}{V}\, \text{d}V = \]Now we perform the integration and substitute the limits
\[=p_2V_2[\ln{V}]_{V_2}^{V_1} = p_2V_2\ln{\frac{V_1}{V_2}}.\]The total work W performed by the cycle will then be given by
\[W=W_1+W_3=p_1\left(V_2-V_1\right)+p_2V_2\ln{\frac{V_1}{V_2}}.\]However, we do not know the values of pressure and volume. We can determine them by using the equation of state for ideal gas:
\[pV=nRT\]and the relation
\[\frac{V_1}{V_2}=\frac{T_1}{T_2}\]that follows from the fact that during isobaric process, the ratio of volume and temperature is constant (Gay-Lussac's Law).
Now we can determine the total work as
\[W=nR\left(T_2-T_1\right)+nRT_1\ln{\frac{T_1}{T_2}}\]and after simplification
\[W= nR\left[T_2-T_1\left(1-\ln{\frac{T_1}{T_2}}\right)\right].\]Hint 3 – Entropy Change
To determine the entropy change ΔS we need to determine the heat absorbed or released by the gas in individual parts of the cycle.
What applies for these heats?
Analysis – Entropy Change
First, we determine the heats and related entropy changes in individual parts of the cycle. We need to realize when the heat is absorbed (entropy increases) and when it is given off (entropy decreases) by the gas.
During isobaric expansion the temperature of the gas increases and the gas performs work. From the First Law of Thermodynamics therefore follows that the heat is absorbed by the gas. To determine entropy change we need to use integral calculus due to the fact that temperature changes during this process.
During isochoric cooling the system does not perform work and internal energy of the gas decreases. This means that during this process the gas gives off heat to the surroundings. Since during this proces the temperature is not constant, we need to use integral calculus to determine entropy change.
During isothermal compression the work is performed by the surroundings. The internal energy of the gas does not increase. According to the Fisrt Laf of Thermodynamics the gas must be giving off heat and entropy decreases. Since during this process the temperature is constant, we can determine entropy change as a ratio of given-off heat and temperature at which the process is happening.
Solution – Entropy Change
We will now determine heats Qi and related entropy changes ΔSi in individual parts of the cycle. We need to realize when the heat is absorbed by the gas and when it is given off.
During isobaric expansion temperature increases and gas performs work. From the First Law of Thermodynamic follows that heat Q1 is absorbed by the gas. It applies
\[Q_1=C_pn\left(T_2-T_1\right),\]where Cp is molar heat capacity at constant pressure, n is amount of substance and T1, T2 initial and final temperature.
The folowing applies for molar heat capacity at constant volume CV of two-atom gas:
\[C_V=\frac{5}{2}R,\]where R is the molar gas constant.
Using Meyer's relation Cp = CV + R we obtain for molar heat capacity at constant pressure:
\[C_p=\frac{5}{2}R+R=\frac{7}{2}R.\]For heat Q1 supplied to the gas it is therefore true
\[Q_1=\frac{7}{2}nR\left(T_2-T_1\right).\]Now we can determine entropy change ΔS1 during this process. We need to realize that temperature T is not constant and therefore we cannot determine the entropy change as a ratio of total heat Q1 and temperature. We must use integral calculus.
For elementary entropy change dS1 it applies
\[\text{d}S_1=\frac{\text{d}Q_1}{T}=\frac{7nR\,\text{d}T}{2T}. \]The total entropy change ΔS1 can be the obtained by integration of this relation in the limits from T1 to T2
\[ \Delta S_1= \int\limits_{T_1}^{T_2}\,\text{d}S_1 =\int\limits_{T_1}^{T_2}\frac{7}{2}\frac{nR}{T}\,\text{d}T = \]We factor the constants out of the integral
\[=\frac{7}{2}nR\int\limits_{T_1}^{T_2}\frac{\text{d}T}{T}= \]Now we perform the integration and substitute the limits
\[=\frac{7}{2}nR\left[\ln{T}\right]_{T_1}^{T_2} = \frac{7}{2}nR\ln{\frac{T_2}{T_1}}.\]During isochoric cooling the system does not perform work and internal energy of the gas decreases. This means that during this process the system gives off heat Q2 to its surroundings:
\[Q_2=C_Vn\left(T_1-T_2\right)=\frac{5}{2}nR\left(T_1-T_2\right).\]Since during this process temperature is not constant, we write the relation for elementary entropy change dS2 and perform the integration in the limits from T2 to T1. Entropy change ΔS2 is given by:
\[ \Delta S_2= \int\limits_{T_2}^{T_1}\,\text{d}S_2 =\int\limits_{T_2}^{T_1}\frac{5}{2}\frac{nR}{T}\,\text{d}T = \]We factor the constants out of the integral
\[=\frac{5}{2}nR\int\limits_{T_2}^{T_1}\frac{\text{d}T}{T}= \]we perform the integration and substitute the limits
\[=\frac{5}{2}nR\left[\ln{T}\right]_{T_2}^{T_1} = \frac{5}{2}nR\ln{\frac{T_1}{T_2}} = -\frac{5}{2}nR\ln{\frac{T_2}{T_1}}.\]Entropy change is negative because the system gives off heat.
Now we determine entropy change ΔS3 during isothermal compression. As we have already stated in the upper part of the task, the work is performed by the surroundings. Internal energy if the gas does not increase. According to the First Law of Thermodynamics, the gas must give off heat Q3, therefore entropy change will again be negative. Entropy therefore decreases. Since during this proces the temperature is constant and equal to T1, we can determine entropy change ΔS3 as
\[\Delta S_3=\frac{Q_3}{T_1}.\]During isothermal processes it applies that according to the First Law of Thermodynamics the given-off heat is equal to the performed work. For ΔS3 we obtain:
\[\Delta S_3=\frac{Q_3}{T_1}=\frac{W_3}{T_1} = \frac{nRT_1\ln{\frac{T_1}{T_2}}}{T_1} = nR\ln{\frac{T_1}{T_2}} = -nR\ln{\frac{T_1}{T_2}}.\]Now we can determine the total entropy change ΔS of the whole cycle. It applies
\[\Delta S=\Delta S_1+\Delta S_2+\Delta S_3\] \[\Delta S=\frac{7}{2}nR\ln{\frac{T_2}{T_1}} - \frac{5}{2}nR\ln{\frac{T_2}{T_1}} - nR\ln{\frac{T_2}{T_1}}=0.\]This means that entropy change during the whole cycle is zero. We could have made this conclusion without long calculation because entropy is a state function. If gas returns to its original state after performing one cycle, it has to have the same entropy and its change is therefore zero. We have confirmed this fact by the calculation.
Hint 4 – Efficiency
What is the definition of efficiency of a heat engine (in general) and efficiency of Carnot engine?
Analysis – Efficiencies η and ηid
We write a relation for heat cycle efficiency (in general) and for Carnot cycle efficiency. Then we will compare determined values.
The efficiency of Carnot cycle should be higher. This is due to the fact that Carnot ideal cycle has maximal efficiency for given temperatures of heater and cooler.
Solution – Efficiencies η and ηid
Efficiency η is defined as a ratio of total work W performed by the cycle and heat Qsup supplied to the gas, ergo
\[\eta=\frac{W}{Q_{sup}}.\]Work W has already been determined. Since gas only absorbs heat during isobaric expansion, it holds Qsup = Q1.
The efficiency is therefore determined as follows
\[\eta=\frac{W}{Q_1} = \frac{nR\left[T_2-T_1\left(1-\ln{\frac{T_1}{T_2}}\right)\right]}{\frac{7}{2}nR\left(T_2-T_1\right)} = \frac{T_2-T_1\left(1-\ln{\frac{T_1}{T_2}}\right)}{\frac{7}{2}\left(T_2-T_1\right)}.\]Now we determine the efficiency ηid of ideal Carnot cycle working between the same temperatures. It applies
\[\eta_{id}=\frac{T_2-T_1}{T_2}.\]Numerical Solution
Total work performed:
\[W= nR\left[T_2-T_1\left(1-\ln{\frac{T_1}{T_2}}\right)\right]\] \[W= 1\cdot{ 8.31}\cdot \left[1000-300\cdot \left(1-\ln{\frac{300}{1000}}\right)\right]\,\mathrm{J}\dot{=}2815\,\mathrm{J}\dot{=}2.8\,\mathrm{kJ}\]Efficiency of given cycle:
\[\eta= \frac{T_2-T_1\left(1-\ln{\frac{T_1}{T_2}}\right)}{\frac{7}{2}\left(T_2-T_1\right)}\] \[\eta = \frac{1000-300\cdot \left(1-\ln{\frac{300}{1000}}\right)}{\frac{7}{2}\cdot \left(1000-300\right)}\dot{=}0.14\]Efficiency of ideal Carnot cycle:
\[\eta_{id}=\frac{T_2-T_1}{T_2}\] \[\eta_{id}=\frac{1000-300}{1000}=0.7\]We can see that Carnot cycle working between the same temperatures would have had much higher efficiency than our given cycle. This is in agreement with the fact that Carnot ideal cycle has the maximum efficiency for given heater and cooler temperatures.
Answer
Total work performed by the cycle is approximately 2.8 kJ.
Total entropy change of the cycle is zero.
Cycle efficiency is approximately 0.14.
Carnot cycle efficiency is 0.7.
Pressure-Volume Diagram