Generator napięcia przemiennego (sinusoidalnego natychmiastowego)
Kod zadania: 1009
Generator napięcia zmiennego u(t) = 25sin(377t) jest połączony z cewką o indukcyjności 12,7 H.
Uwaga: W równaniu napięcia chwilowego nie piszemy jednostki. Bierzemy jednostki podstawowe tzn. podstawiamy czas w sekundach itd.
Zapis danych
Dane:
Chwilowe napięcie generatora: u(t) = 25sin(377t) Indukcyjność cewki: L = 12,7 H Szukane:
a) Amplituda prądu: Im = ? (A) b) Napięcie, w chwili gdy prąd jest maksymalny: Ub = ? (V) c) Natężenie prądu przy napięciu Uc = 12,5 V: Ic = ? (A) Podpowiedź 1
Zastanów się, jakie wielkości fizyczne we wzorze na napięcie chwilowe są wyrażone wartościami liczbowymi.
Podpowiedź 2
W celu obliczenia maksymalnej wartości prądu, amplitudy prądu, skorzystaj z prawa Ohma dla prądu zmiennego.
Podpowiedź 3
Jakie jest przesunięcie fazowe napięcia prądu, jeżeli w obwodzie znajduje się cewka?
Analiza
Zadanie jest podzielone na trzy części, które będziemy stopniowo rozwiązywać.
a) Jeżeli znamy przebieg chwilowego napięcia w obwodzie, znamy także amplitudę. Amplitudę prądu (czyli maksymalne natężenie prądu) otrzymamy z prawa Ohma. Impedancję w prawie Ohma stanowi opór indukcyjny cewki, który może być wyznaczony z indukcyjności cewki znajdującej się w obwodzie.
b) Po pierwsze należy wyznaczyć wartość chwilowego natężenia prądu w obwodzie. W układzie tym znajduje się cewka, co oznacza, że napięcie jest przesunięte w fazie o π/2. Następnie określamy czas, w którym natężenie prądu osiąga maksymalną wartość. Zastępujemy czas we wzorze na napięcie chwilowe.
c) Postępowanie w tym zadaniu będzie podobne do tego w p-cie b). Chwilowy czas t, w którym napięcie wynosi 12,5 V. Ze względu na funkcję sinus otrzymamy kilka czasów, którym odpowiada ta sama wartość napięcia.
Analiza wzoru do opisu chwilowego napięcia
Porównując ogólny wzór na wartość chwilowego napięcia z napięciem podanym w treści zadania:
\[u(t)=U_m\sin(\omega t+ {\varphi}_{0u})=25\sin(377t)\]
widzimy, że:
\[U_m=25\,\mathrm V\]
\[\omega=377\,\mathrm s^{-1}\]
Rozwiązanie 1
Zastosujmy prawo Ohma
\[I_m=\frac{U_m}{Z}\]Za opór podstawmy opór indukcyjny cewki:
\[I_m=\frac{U_m}{Z}=\frac{U_m}{X_L}=\frac{U_m}{\omega L}\]
Podstawiając wartości otrzymamy:
\[I_m=\frac{25}{377 \cdot{ 12{,}7}}\,\mathrm A\,\dot{=}\,5{,}2 \,\mathrm {mA}\]Rozwiązanie 2
Napiszmy równanie na chwilową wartość natężenia prądu. Amplitudę prądu obliczono w p-cie a). Przesunięcie fazowe między natężeniem prądu a napięciem wynosi – π/2, ponieważ w obwodzie jest cewka.
\[i(t)=I_m \sin(\omega t + {\varphi}_{0i})=5{,}2 {\cdot} 10^{-3}\sin(377t- \frac{\pi}{2})\]
Chcemy znaleźć czas, w którym natężenie prądu jest maksymalne i(t) = Im:
\[i(t)=I_m\sin(377t-\frac{\pi}{2})\]
\[I_m=I_m\sin(377t-\frac{\pi}{2})\]
\[1=\sin(377t-\frac{\pi}{2})\]
\[\frac{\pi}{2}=377t-\frac{\pi}{2}\]
\[t=\frac{\pi}{377}\,\mathrm s\]
Napięcie przy maksymalnym natężeniu prądu otrzymamy podstawiając czas do wzoru na napięcie chwilowe:
\[U_b=25\sin(377t)=25\sin(377 \cdot \frac{\pi}{377})\mathrm V=25\sin(\pi)\,\mathrm V=0\,\mathrm V\]
Zerową wartość napięcia przy maksymalnym natężeniu prądu możemy przewidzieć bez liczenia, ponieważ chwilowe wartości napięcia i natężenia prądu opisuje funkcja sinus. Obecność w obwodzie cewki spowoduje przesunięcie o π/2, więc jeśli jedna z sinusoid będzie miała maksimum, wówczas druga przyjmie minimum. Zobacz rysunek w dalszej części zadania.
Rozwiązanie 3
Chcemy wyznaczyć wartość natężenia prądu przy napięciu Uc = 12,5 V.
\[U_c=25\sin(377t)\]
\[12{,}5=25\sin(377t)\]
\[\sin(377t)=\frac{1}{2}\]
Zadanie rozwiążemy dla pierwszego przedziału czasu tj. dla okresu opisującej wartość chwilowego napięcia. Dla kolejnych okresów otrzymamy takie same wyniki. Uzyskujemy dwa czasy, dla których napięcia osiągają pożądaną wartość:
\[377t= \frac{\pi}{6 }\,\mathrm s \tag{1}\]
\[377t= \frac{5\pi}{6 }\,\mathrm s \tag{2}\]
Wartości możemy zobaczyć (odczytać) na rysunku przedstawiającym zależność napięcia i natężenia prądu od czasu.
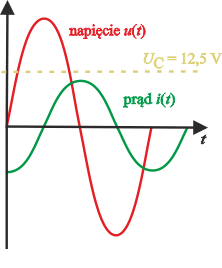
Na rysunku żółtą linią zaznaczono napięcie 12,5 V.
Wartość, której szukamy: \(377t= \frac{5\pi}{6 }\,\mathrm s \), ponieważ napięcie jeszcze bardziej spadnie.
Podstawiając czas do wzoru na chwilową wartość prądu otrzymamy wartość prądu dla napięcia 12,5 V:
\[I_c=5{,}2 \cdot {10^{-3}}\sin(377t- \frac{\pi}{2})=5{,}2 \cdot {10^{-3}}\sin( \frac{5\pi}{6 } - \frac{\pi}{2})\,\mathrm A=\] \[\ =5{,}2 \cdot {10^{-3}}\sin(\frac{\pi}{3})\,\mathrm A\,\dot{=}\,4{,}5\,\mathrm {mA} \]
Odpowiedź
Maksymalna wartość natężenia prądu wynosi: Im = 5,2 mA.
Przy maksymalnym natężeniu prądu jego napięcie wynosi zero: Ub = 0 V.
Jeżeli napięcie wynosi 12,5 V i dalej będzie spadać to jego natężenie wynosi: Ic = 4,5 mA.



