Zbiór rozwiązanych zadań i problemów fizycznych

Potencjometr

Kod zadania: 542

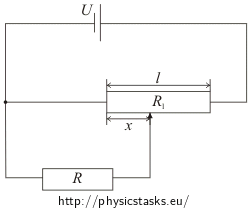
Potencjometr wykonany z materiału o oporze właściwym jednorodnym na całej długości l oraz opór R_l = al zmienia napięcie w urządzeniu o oporze R.

Znajdź napięcie i natężenie prądu płynącego przez opornik R i wyraź go jako funkcję odległości x od końca potencjometru.

• Podpowiedź

  Spróbuj narysować obwód tak, aby potencjometr był podzielony na dwie części.

• Analiza

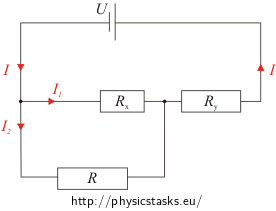
  Narysujmy jeszcze raz obwód z potencjometrem podzielonym na dwie części z oporami R_x i R_y (spójrz na rysunek). Możemy znaleźć opór każdej części. Opór przewodnika jest funkcją liniową jego długości, a opór części potencjometru jest proporcjonalny do długości przewodu w tej części potencjometru.

  Określmy natężenia prądów płynących przez oczka pokazane na rysunku.

  Potrzebne będzie natężenie I₂ przepływające przez opornik R, ponadto wyrazimy wszystkie natężenia jako funkcje I₂. Natężenie I jest sumą natężeń I₁ i I₂. Oporniki R i R_x są połączone równolegle, więc napięcia na tych opornikach muszą być równe. Pomaga to w wyrażeniu natężenia I₁ jako funkcji I₂.

  Znamy napięcie w całym obwodzie, stąd możemy wyznaczyć SEM (siłę elektromotoryczną) jako sumę spadków napięć między opornikami R_x i R_y.

  Z wyrażenia na całkowite napięcie wyznaczymy natężenie I₂.

  Napięcie w oporniku R jest dane jako produkt oporu opornika i natężenie prądu przepływającego przez opornik.

• Rysunek

  

• Rozwiązanie

  Opór potencjometru opisuje wyrażenie:

  \[R_x+R_y\,=\,R_l\,=\,al\]

  gdzie l – długość całego potencjometru, a – wartość stała, współczynnik proporcjonalności.

  Opór przewodu jest funkcją liniową, dzięki której możemy wyrazić opory R_x i R_y jako:

  \[R_x\,=\,ax\] \[R_y\,=\,a\left(l-x\right)\]

  Naszym celem jest znalezienie natężenia I₂ prądu przepływającego przez opornik R oraz zapisanie pozostałych natężeń jako funkcji natężenia I₂.

  Algebraiczna suma prądów w węźle jest równa zero.

  \[I\,=\,I_1+I_2\]

  Opornik o oporze R i część potencjometru o oporności R_x są połączone równolegle, więc:

  \[RI_2\,=\,R_xI_1\,=\,axI_1\]

  Możemy zapisać I₁ jako:

  \[I_1\,=\,\frac{R}{ax}I_2\tag{*}\]

  Skoro znane jest napięcie prądu płynącego w obwodzie możemy zapisać SEM (siłę elektromotoryczną) jako sumę spadków napięć na opornikach. Stąd:

  \[U\,=\,R_xI_1+R_yI\,=\,axI_1+a\left(l-x\right)\left(I_1+I_2\right)\] \[U\,=\,alI_1+a\left(l-x\right)I_2\]

  Wstawiając równanie (*) do powyższego otrzymujemy:

  \[U\,=\,al\frac{R}{ax}I_2+a\left(l-x\right)I_2\] \[U\,=\,\left(\frac{l}{x}R+a\left(l-x\right)\right)I_2\]

  Wyznaczamy współczynnik proporcjonalności a z równania:

  \[R_l\,=\,al\hspace{10px}\Rightarrow\hspace{10px}a\,=\,\frac{R_l}{l}\]

  i wstawiamy do wyrażenia opisującego napięcie:

  \[U\,=\,\left(\frac{l}{x}R+\frac{R_l}{l}\left(l-x\right)\right)I_2\]

  Możemy zapisać natężenie prądu I₂ przepływającego przez opornik R:

  \[I_2\,=\,\frac{U}{\frac{l}{x}R+\frac{R_l}{l}\left(l-x\right)}\]

  i upraszczając otrzymamy:

  \[I_2\,=\,\frac{U}{\frac{l^2R+R_lx\left(l-x\right)}{xl}}\]

  Ostatecznie równanie opisujące zależność natężenia prądu jako funkcji odległości x od końca potencjometru:

  \[I_R\,=\,\frac{xlU}{l^2R+R_lx\left(l-x\right)}\]

  Napięcie prądu przepływającego przez opornik zależy od natężenia i oporu opornika:

  \[U_R\,=\,I_RR\]

  czyli

  \[U_R\,=\,\frac{xlUR}{l^2R+R_lx\left(l-x\right)}.\]

• Odpowiedź

  Napięcie i natężenie prądu przepływającego przez opornik R w zależności od odległości x opisują równania:

  \[I_R\,=\,\frac{xlU}{l^2R+R_lx\left(l-x\right)},\] \[U_R\,=\,\frac{xlUR}{l^2R+R_lx\left(l-x\right)}.\]