Węgorz elektryczny
Kod zadania: 540
Węgorz elektryczny (Electrophorus electricus), żyje w rzekach Ameryki Południowej. Żywi się rybami, które zabija poprzez elektryczne wstrząsy. Węgorz elektryczny generuje napięcie elektryczne w specjalnych układach komórek nazywanych elektroblastami.
Ciało węgorza elektrycznego zbudowane jest w przybliżeniu z 700 000 elektroblastów. Można przyjąć, że elektroblast jest źródłem napięcia elektrycznego o wartości Ue = 0,15 V i wewnętrznym oporze Re = 0,25 Ω. Załóżmy, że woda wokół węgorza ma oporność Rv = 800 Ω.
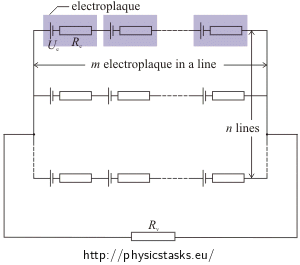
a) Załóżmy, że elektroblasty są ułożone w n – liniach i w każdej z nich znajduje się m elektroblastów. Znajdź liczby n i m tak, aby przepływający prąd od głowy do ogona węgorza miał maksymalną wartość.
b) Jak duży może być ten prąd (jego natężenie)?
Podpowiedź 1
Zastanów się, w jaki sposób policzyć napięcie prądu oraz opór układu oporników połączonych równolegle oraz szeregowo.
Podpowiedź 2
Sprawdź, jak wyznaczyć maksimum funkcji korzystając z jej pochodnej.
Rysunek
Narysuj schemat połączonych ze sobą elektroblastów.
n - ilość linii połączonych równolegle m - ilość komórek połączonych szeregowo w jednej linii N = n·m - ilość wszystkich elektroblastów Ue - napięcie prądu wytwarzanego przez jeden elektroblast Re - wewnętrzny opór elektryczny jednej komórki Rv - opór wody otaczającej węgorza Analiza – maksimum funkcji
Ekstremum (minimum lub maksimum) funkcji f(x) jest położone w punktach stacjonarnych lub w punktach, które nie są różniczkowalne.
Punkty stacjonarne funkcji f(x) to punkty a, w których pierwsza pochodna jest zerem:
\[f' \left(a\right)\,=\,0 \]Analiza – rozwiązanie
Skorzystamy z prawa Ohma, aby znaleźć prąd przepływający przez wodę wokół węgorza. Wyjaśnijmy, że całkowite natężenie i całkowity opór elektryczny oraz wewnętrzny obejmuje wyrażenie całkowitego natężenia jako funkcję ilości elektroblastów w linii.
Maksymalna ilość komórek w jednej linii, przez które przepływa prąd do wody począwszy od głowy a kończąc na ogonie węgorza, jest określona przez pochodną. Otrzymaną wartość podstawiamy do ogólnego równania na natężenie prądu. Wynikiem jest maksimum natężenia prądu, którego szukamy.
Część pierwsza rozwiązania – całkowite natężenie
Wyznaczamy całkowite natężenie prądu korzystając z prawa Ohma:
\[I_\mathrm{calkowite}\,=\,\frac{U_\mathrm{calkowite }}{R_{z}}\]Dla oporników połączonych równolegle napięcie na każdym z nich jest identyczne. Dla oporników połączonych szeregowo napięcie całkowite jest sumą napięć na wszystkich opornikach. Całkowite napięcie wytwarzane przez komórki jest równe:
\[U_\mathrm{calkowite }\,=\,m U_e\]Całkowity opór jest sumą oporu wody Rv oraz oporu ciała węgorza R.
Opór komórek ułożonych szeregowo – liniowo jest równe: \(R_r\,=\,m R_e\)
Opór ciała węgorza opisuje zależność (dla n elektroblastów połączonych równolegle):
\[\frac{1}{R}\,=\,\frac{n}{R_r}\,=\,\frac{n}{mR_e}\,\Rightarrow\,R\,=\,\frac{m}{n}R_e\,.\]Całkowity opór obwodu: \(R_{z}\,=\,R_v+R\,=\,R_v+\frac{m}{n}R_e\).
Można teraz wyznaczyć całkowite natężenie prądu Icałkowite:
\[I_\mathrm{calkowite}\,=\,\frac{U_\mathrm{calkowite}}{R_{z}}\,=\,\frac{m U_e}{\frac{m}{n}R_e+R_v} \,=\, \frac{n m U_e}{mR_e+nR_v}\]Skoro \(n m \,=\, N \), więc \(n\,=\, \frac{N}{m}\) i możemy zapisać zależność:
\[I_\mathrm{calkowite}\,=\,\frac{NU_e}{mR_e+\frac{NR_v}{m}}\]Jest to wyrażenie opisujące całkowite natężenie Icałkowite, w którym jedyną zmienną jest m.
Część druga rozwiązania – maksymalna wartość m
Znamy całkowite natężenie prądu płynącego przez wodę od głowy węgorza:
\[I_\mathrm{calkowite}\,=\,\frac{NU_e}{mR_e+\frac{NR_v}{m}}\]Należy znaleźć taką wartość m , aby całkowite natężenie prądu Icalkowite miało maksymalną wartość. Licznik powyższego równania jest wielkością stałą (ponieważ nie zależy od m), więc całe równanie przyjmie wartość maksymalną, gdy mianownik będzie miał minimalną wartość.
Poszukiwaną wartość można znaleźć wyliczając pochodną mianownika ze względu na m,
\[\frac{d}{dm}\left(mR_e+\frac{NR_v}{m}\right)\,=\,R_e+NR_v\left(-\frac{1}{m^2}\right) \,=\,R_e-\frac{NR_v}{m^2}\,,\]przyrównujemy powyższe wyrażenie do zera:
\[R_e-\frac{NR_v}{m^2}\,=\,0\]wyznaczamy m:
\[m^2R_e-NR_v\,=\,0\] \[{m}^2R_e\,=\,NR_v\]\(m\,=\,\pm \sqrt{\frac{R_v}{R_e}N}\), ujemna wartość m nie ma sensu fizycznego, więc ją pomijamy.
Prąd ma maksymalne natężenie, gdy:
\[m\,=\,\sqrt{\frac{R_v}{R_e}N}\]Część trzecia rozwiązania – obliczenia
Część a)
Dla komórek połączonych szeregowo:
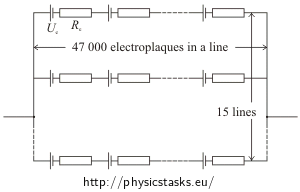
\[m\,=\,\sqrt{\frac{R_v}{R_e}N}\] \[m\,=\,\sqrt{\frac{800}{0{,}25}\cdot 700\,000}\,\dot{=}\,47\,000 \]Dla n:
\[n\,=\,\frac{N}{m}\,=\,\frac{700\,000}{47\,000}\] \[n\,\dot{=}\,15\]Część b)
Maksymalne natężenie prądu znajdujemy poprzez wstawienie otrzymanej wartości m do wyrażenia na natężenie prądu uzyskanego w pierwszej części rozwiązania:
\[I_\mathrm{calkowite} \,=\, \frac{NU_e}{mR_e+\frac{NR_v}{m}}\]Stąd:
\[I_{max}\,=\,\frac{700\,000\,\cdot \,0{,}15}{47\,000\,\cdot \,0{,}25 + \frac{700\,000\,\cdot \,800}{47\,000}}\, \mathrm{A}\] \[I_{max}\,\dot{=}\,4{,}4\,\mathrm{A}\]Odpowiedź
a) Aby natężenie prądu płynącego przez wodę było maksymalne, cały obwód powinien zawierać 15 (odgałęzień) połączeń równoległych. Każda z gałęzi powinna obejmować około 47000 komórek elektroblastów połączonych szeregowo.
b) Całkowite natężenie prądu płynącego przez wodę, a wytwarzanego przez taki układ komórek (jak na rysunku) jest równy około 4,4 A.
Jak jest w rzeczywistości?
W rzeczywistości jest jednak trochę inaczej.
Komórki są ułożone w liniach wzdłuż ciała węgorza. Każda z linii zawiera od 5000 do 6000 komórek połączonych szeregowo. Węgorz elektryczny może wytworzyć napięcie około 600 V, a natężenie prądu wokół węgorza może osiągnąć wartość 1 A.
Jak to jest możliwe, że węgorz nie rani ani nie zabija samego siebie?
Dzieje się tak, dlatego że natężenie prądu płynącego przez każdą linię komórek jest małe, około dwa razy mniejsze niż natężenie prądu przepływającego przez wodę. Ponadto ciało węgorza jest chronione przez grubą skórę.
Tylko w przypadku zranienia, węgorz może się zabić poprzez porażenie prądem.
Podsumowanie metod obliczeniowych pochodnych wybranych funkcji
Funkcja Uwaga Pochodna \[f\left(x\right)\,=\,c\]
c to stała \[f'\left(x\right)\,=\,0\]
\[f\left(x\right)\,=\,cx\]
c to stała \[f'\left(x\right)\,=\,c\]
\[f\left(x\right)\,=\,x^c\]
c to stała \[f'\left(x\right)\,=\,cx^{c-1}\]
Pochodna sumy dwóch funkcji f, g, a, b stałe:
\[\left(af+bg\right)'\,=\, af'+ bg'\]Pochodna iloczynu dwóch funkcji f, g:
\[\left(fg\right)'\,=\,f'g+fg'\]Pochodna ilorazu dwóch funkcji f, g, gdzie g ≠ 0:
\[\left(\frac{f}{g}\right)'\,=\,\frac{f'g-fg'}{g^2}\]