Stałe pole elektryczne - natężenie pola w wierzchołku trójkąta
Kod zadania: 1003
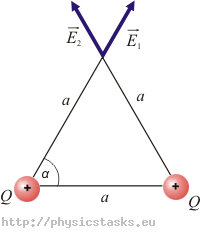
W dwóch wierzchołkach trójkąta równobocznego, którego ramiona mają długość 0,5 m, umieszczono jednakowe ładunki, każdy o wartości 1 µC.
Oblicz natężenie pola elektrostatycznego w trzecim wierzchołku tego trójkąta.
Podpowiedź 1
Całkowite natężenie pola elektrostatycznego otrzymuje się przez zsumowanie natężeń pochodzących od poszczególnych ładunków. Wykonaj rysunek.
Podpowiedź 2
Natężenie pola elektrostatycznego ma taki sam kierunek jak siła, która działa na umieszczony w danym punkcie ładunek dodatni.
Rysunek
Analiza
Całkowite natężenie pola elektrostatycznego w wierzchołku trójkąta dane jest przez wektorową sumę natężeń od poszczególnych ładunków. Ładunki mają tę samą wartość i znajdują się w takiej samej odległości od miejsca, w którym chcemy ustalić natężenie pola, wektory natężenia mają tę samą długość. Kierunek wektora natężenia pola elektrostatycznego jest taki sam, jak kierunek siły działającej na umieszczony w wierzchołku trójkąta ładunek próbny. Wektor natężenia pola elektrostatycznego będzie więc miał zwrot na zewnątrz trójkąta.
Rozwiązanie
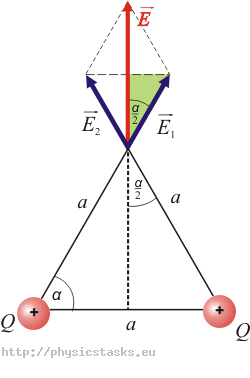
Całkowite natężenie pola elektrostatycznego otrzymamy sumując wektorowo natężenia, które wytworzyły poszczególne ładunki.
Natężenia \(\vec{E}_1\) a \(\vec{E}_2\)mają stałą wartość, ponieważ oba ładunki mają stałą wartość i znajdują się w tej samej odległości od miejsca, gdzie szukamy wartości natężenia. Ponieważ oba ładunki są dodatnie, natężenie skierowane jest „na zewnątrz”.
Trójkąt jest równoboczny, dzięki czemu znamy miarę kąta α = 60°
Z „zielonego“trójkąta prostokątnego otrzymamy cosinus kąta α/2
\[\cos{\frac { \alpha}{2}}\,=\,\frac{\frac {E}{2}}{E_1}.\]Po przekształceniu, którego otrzymamy wyrażenie na nieznaną wartość natężenia pola elektrostatycznego E
\[E\,=\,2E_1\cos \frac{\alpha}{2}\tag{*}\]Natężenie E1 otrzymamy ze stosunku:
\[E_1\,=\,k \, \frac{Q}{r^2}\, ,\]gdzie r jest odległością ładunku od punktu, w którym badamy natężenie. W naszym przykładzie ta odległość oznaczona jest przez a. Ostatni związek podstawiamy do wzoru (*)
\[E\,=\,2k\, \frac {Q}{a^2} \,\cos \frac{\alpha}{2}\]Dane i podstawienie wartości liczbowych
\[a\,=\,0{,}5 \,\mathrm{m}\] \[Q\,=\,1\,\mathrm{\mu C}\,=\,10^{-6}\,\mathrm{C}\] \[E\,=\,?\,\left(\mathrm{kV\,m^{-1}}\right)\]Z tabeli:
\[k\,=\, 9 \cdot {10^9}\,\mathrm{kg\,m^2\,s^{-2}\,C^{-1}}\]
\[E\,=\,2k\, \frac {Q}{a^2} \,\cos \frac{\alpha}{2}\] \[E\,=\,2\,\cdot\,9\cdot {10^9}\,\cdot\,\frac{10^{-6}}{0{,}5^2}\,\cdot\,\cos{\frac{60°}{2}}\,\mathrm{V\,m^{-1}}\,=\,\frac{18\cdot{10^3}}{0{,}25}\cdot\frac{\sqrt3}{2}\,\mathrm{V\,m^{-1}}\] \[E\,=\,6{,}2 \cdot{10^4} \, \mathrm{V\,m^{-1}}\,=\,62 \, \mathrm{kV\,m^{-1}}\]Odpowiedź
W trzecim wierzchołku trójkąta wektor natężenia pola elektrostatycznego będzie skierowany „do góry” a wartość natężenia będzie wynosiła:
\[E\,=\,2k\, \frac {Q}{r^2} \,\cos \frac{\alpha}{2}\,=\,62 \, \mathrm{kVm^{-1}}\]Co się zmieni, jeżeli oba ładunki będą ujemne?
Wartości wektorów natężenia \(\vec{E}_1\) i \(\vec{E}_2\)nie zmieniły się, ponieważ ładunki mają stałą wartość, a ich odległość się nie zmieniła. Ale zwrot wektorów będzie przeciwny, ponieważ oba ładunki są ujemne.
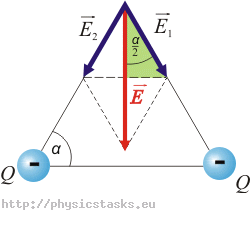
Dalsze postępowanie będzie takie samo. Całkowita wartość natężenia nie powinna ulec zmianie, ale zwrot wektora powinien być przeciwny niż w przypadku dwóch ładunków dodatnich.