Szeregowy obwód RLC
Kod zadania: 1045
Obwód prądu zmiennego tworzą połączone szeregowo:

Zapis danych
Wypiszmy wielkości, które znamy :
Opór opornika R = 50 Ω Indukcyjność cewki L = 0,3 H Pojemność kondensatora C = 15 μF =15·10-6 F Amplituda napięcia źródła Um = 25 V Częstotliwość f = 50 Hz Połączenie opornika, cewki i kondensatora jest szeregowe.Wielkości, których szukamy :
Amplituda natężenia prądu w obwodzie Im = ? (A) Przesunięcie fazowe pomiędzy napięciem i natężeniem φ = ? (°) Analiza zadania
Metoda rozwiązywania:
- Obliczmy wartość amplitudy natężenia prądu. Skorzystamy z prawa Ohma dla prądu zmiennego, które określa związek pomiędzy całkowitym oporem (zawadą) Z, amplitudą napięcia Um i amplitudą natężenia Im . Wszystkie niezbędne do obliczenia wielkości są dane.
- Ponieważ wszystkie elementy obwodu połączono szeregowo, płynie przez nie prąd zmienny, w którym napięcie jest przesunięte w fazie w stosunku do natężenia. Aby określić wartość tego przesunięcia, skorzystamy z diagramu fazowego.
Metoda kreślenia diagramu fazowego
Przy pomocy strzałek będziemy zaznaczać napięcia i natężenia prądu na poszczególnych elementach obwodu. Długość takiego "wektora" (fazora) odpowiada amplitudzie, kierunki i zwroty obrazują przesunięcia w fazie.
Metoda kreślenia diagramu fazowego dla obwodu:
Diagram fazowy opierać się będzie na odpowiednich miarach napięcia i natężenia prądu w obwodzie.- We wszystkich elementach obwodu szeregowego popłynie prąd o jednakowym natężeniu, niech więc wspólny "wektor" Im będzie miał kierunek i zwrot zgodny ze zwrotem osi x.
- Fazor napięcia na oporniku UR ma zwrot zgodny z fazorem natężenia. Na rysunku zaznaczono go na zielono.
- Napięcie na cewce UL „poprzedza“ natężenie o π/2 (ćwierć okresu), dlatego też jego fazor skierujemy „w górę“ – a więc zgodnie ze zwrotem osi y. Na rysunku zaznaczono go kolorem żółtym.
- Napięcie na kondensatorze UC „opóźnia się“ w stosunku do natężenia o π/2, dlatego też jego fazor skierujemy „w dół“. Zaznaczono go kolorem różowym.
- Amplitudę całkowitego napięcia otrzymamy jako „sumę wektorową“ fazorów napięcia na różnych elementach obwodu. Najpierw odejmijmy od siebie napięcia na cewce UL i kondensatorze UC (na rysunku wynik zaznaczono kolorem fioletowym). Następnie otrzymany wynik dodajemy wektorowo do napięcia na oporniku UR. Fazor amplitudy całkowitego napięcia zaznaczono kolorem jasno niebieskim.
- Przesunięciu fazowemu między napięciem a natężeniem prądu odpowiada kąt φ, który tworzą fazory natężenia i całkowitego napięcia. Na rysunku kąt φ zaznaczono kolorem ciemno niebieskim.
Dla zadanego obwodu RLC diagram fazowy wygląda jak poniżej:
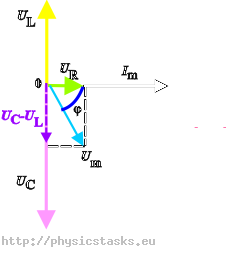
Określenie wzoru na opór całkowity (zawadę) Z z diagramu fazowego
Chcąc uzyskać z diagramu fazowego wyrażenie na opór całkowity Z, wprowadźmy do diagramu fazowego w miejsce napięć opory: indukcyjny XL, pojemnościowy XC i omowy R.
Z prawa Ohma: \( U_C=I_m X_C, \) \( U_L=I_m X_L,\) \( U_R=I_m R. \)
Ponieważ w obwodzie szeregowym przez wszystkie jego elementy płynie prąd o jednakowym natężeniu, możemy wykonać diagram bardzo podobny jak dla fazorów napięcia.
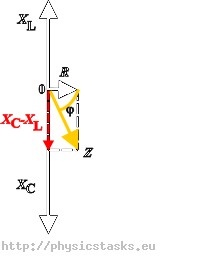
Aby określić wartość oporu całkowitego Z, korzystamy z odpowiedniego trójkąta prostokątnego, zapisując twierdzenie Pitagorasa.
\[ Z^2=R^2+(X_C-X_L)^2 \]
Albo:
\[ Z^2=R^2+(X_L-X_C)^2 .\]
Różnica między wyrażeniami polega na tym, czy natężenie prądu poprzedza napięcie, czy też jest na odwrót. Nie ma to jednak wpływu na wartość Z.
Po podstawieniu wyrażeń na opór indukcyjny i pojemnościowy otrzymamy ostatecznie:
\[ Z= \sqrt{R^2+(X_L-X_C)^2}= \sqrt{R^2+( \omega L- \frac{1}{\omega C})^2} \]
Obliczenie wartości amplitudy natężenia prądu
Wzór na opór całkowity Z z prawa Ohma:
\[ Z=\frac{U_m}{I_m}=\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2} \]
Mamy określić amplitudę natężenia prądu Im. Z powyższego wzoru otrzymujemy:
\[ I_m=\frac{U_m}{\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}} \]
Określenie przesunięcia fazowego z diagramu
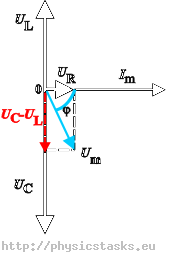

Przesunięcie fazowe na podstawie diagramu określimy jako: \[ \mathrm{tg} {\varphi} = \frac{U_L-U_C}{U_R} =\frac{I_m\omega L- \frac{I_m}{(\omega C)}}{I_mR}=\frac{\omega L-\frac{1}{(\omega C)}}{R}= \frac{X_L-X_C}{R} \]
Niekiedy przy kreśleniu diagramu i określaniu przesunięcia fazowego zamiast wzoru
\[ \mathrm{tg} {\varphi} = \frac{U_L-U_C}{U_R}= \frac{X_L-X_C}{R} \]
stosujemy
\[ \mathrm{tg} {\varphi} = \frac{U_C-U_L}{U_R}= \frac{X_C-X_L}{R} \]
W pierwszym przypadku napięcie poprzedza natężenie, w drugim jest odwrotnie.
Rozwiązanie liczbowe
Amplituda natężenia prądu:
\[ I_m= \frac{U_m}{\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}}= \]
\[ = \frac{25}{\sqrt {50^2+(2 \cdot \pi \cdot 50 \cdot {0{,}3} - \frac{1}{2 \cdot \pi \cdot {50} \cdot {15} \cdot {10^{-6}}})^2}}\,\mathrm{A} \,\dot{=}\, 0{,}2\,\mathrm{A} \]
Przesunięcie fazowe możemy obliczyć znając opory:
\[ \mathrm{tg} {\varphi} = \frac{ \omega L- \frac{1}{ \omega C}}{R} = \frac{ 2 \cdot \pi \cdot {50} \cdot {0{,}3}- \frac{1}{ 2 \cdot \pi \cdot 50 \cdot {15} \cdot {10^{-6}} }}{50} \,\dot{=}\,-2{,}4 \]
Możemy też je określić na podstawie wartości napięć na poszczególnych elementach obwodu:
Napięcia na poszczególnych elementach obwodu wynoszą:
\[ U_R=I_mR\,\dot{=}\,0{,}2 \cdot {50}\,{\mathrm{V}}=10\,\mathrm{V}\]
\[U_L=I_m \omega L\,\dot{=}\, 0{,}2 \cdot{ 2} \cdot {\pi }\cdot {50} \cdot {0{,}3}\,\mathrm{V}\,\dot{=}\, 18{,}85\,\mathrm{V}\]
\[U_C=\frac{I_m}{\omega C}\,\dot{=}\,\frac{0{,}2}{2 \cdot \pi \cdot 50 \cdot {15} \cdot {10^{-6}}}\,\mathrm{V}\,\dot{=}\, 42{,}44\,\mathrm{V} \]
Z diagramu fazowego określmy wartość przesunięcia fazowego:
\[ \mathrm{tg} {\varphi}=\frac{U_L-U_C}{U_R}\,\dot{=} \,\frac{18{,}85-42{,}44}{10}\,\dot{=}\, -2{,}4 \]
Obydwie metody dają ten sam wynik:
\[ \varphi \,\dot{=}\, -67° \]
Znak minus oznacza, że napięcie opóźnia się w stosunku do natężenia.
Odpowiedź
Amplituda prądu w rozważanym obwodzie RLC ma przybliżoną wartość:
Im = 0,2 A.Między napięciem i natężeniem występuje przesunięcie fazowe:
φ = -67°.Ze znaku otrzymanej wartości wnioskujemy, że napięcie opóźnia się w stosunku do natężenia o 67°.



