Chwilowe wartości napięcia i natężenia prądu w szeregowym obwodzie prądu przemiennego RLC
Kod zadania: 1008
Opornik o oporze 90 Ω, cewkę o indukcyjności 1,3 H i kondensator o pojemności 10 μF połączono szeregowo w obwód prądu przemiennego. Jest on podłączony do napięcia zmiennego o amplitudzie 100 V i częstotliwości 50 Hz. Napisz równania na chwilowe wartości napięcia i natężenia prądu płynącego w obwodzie, jeżeli początkowa faza natężenia prądu wynosi zero.
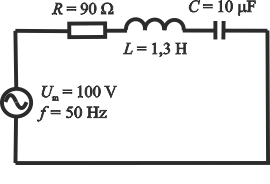
Zapis danych
Z treści zadania wypiszemy wartości, które znamy:
amplituda napięcia zmiennego w obwodzie Um = 100 V częstotliwość prądu przemiennego f = 50 Hz opór opornika R = 90 Ω indukcyjność cewki L = 1,3 H pojemność kondensatora C = 10 μF początkowa faza prądu φ0i = 0 Wartości, które chcemy znaleźć:
chwilowa wartość natężenia prądu i(t) = ? (A) chwilowa wartość napięcia u(t) = ? (V) Podpowiedź 1
Napięcie prądu przemiennego można opisać za pomocą funkcji sinus. Znajdź równanie opisujące chwilową wartość napięcia prądu przemiennego.
Podpowiedź 2
Aby obliczyć amplitudy równań musimy znać aktualną (początkową) wartość \(I_m\) i przesunięcie fazowe pomiędzy napięciem prądu a natężeniem φ0. Skorzystamy z prawa Ohma dla prądu zmienego. Objaśnimy rolę szeregowego obwodu RLC, zamieścimy szczegółowe wyjaśnienie obliczeń i pochodzenie obecnego przesunięcia fazowego.
Amplituda natężenia prądu Im
Stosujemy prawo Ohma dla obwodu prądu zmiennego i podstawiamy wartości:
\[I_m=\frac{U_m}{Z}=\frac{U_m}{\sqrt{R^2+(X_L-X_C)^2}}=\frac{U_m}{\sqrt{R^2+(2 \pi f L - \frac{1}{2 \pi f C})^2}} \]
Obliczamy:
\[I_m=\frac{100}{\sqrt{90^2+(2 \cdot{ \pi} \cdot{ 50} \cdot {1{,}3} - \frac{1}{2 \cdot \pi \cdot {50} \cdot {10} \cdot {10^{-6}}})^2}} \, \mathrm{A} \] \[I_m \,\dot{=}\, 0{,}79 \, \mathrm{A}\]Przesunięcie fazowe między napięciem a natężeniem prądu φ0u
Korzystamy za wzoru, aby wyrazić przesunięcie fazowe za pomocą impedancji każdego z elementów:
\[ \mathrm{tg} \varphi_{0u} = \frac{X_L - X_C}{R}= \frac{\omega L- \frac{1}{ \omega C}}{R}= \frac{2 \pi f L- \frac{1}{ 2 \pi f C}}{R} \] \[\varphi_{0u} =\mathrm{arctg}(\frac{2 \pi f L- \frac{1}{ 2 \pi f C}}{R})\]
Podstawiając wartości liczbowe dostajemy:
\[\varphi_{0u} =\mathrm{arctg}(\frac{2 \pi f L- \frac{1}{ 2 \pi f C}}{R})=\mathrm{arctg}(\frac{2 \cdot \pi \cdot 50 \cdot{ 1{,}3} - \frac{1}{ 2 \cdot \pi \cdot {50} \cdot {10} \cdot {10^{-6}}}}{90})\] \[\varphi_{0u} \,\dot{=}\, 45 ° = \frac{\pi}{4} \]Chwilowe wartości napięcia i natężenia prądu przemiennego
Wartość chwilowego natężenia prądu:
Fazowe przesunięcie prądu jest zerowe, amplituda prądu Im jest obliczona.
\[ i(t)=I_m\sin(\omega t + \varphi_{0i})=I_m\sin( 2 \pi f t + \varphi_{0i} ) \]
\[ i(t)\,\dot {=}\,0{,}79 \cdot \sin(2 \pi 50 t)\,\mathrm A =0{,}79 \cdot \sin(100 \pi t)\,\mathrm A\]
Wartość chwilowego napięcia prądu:
Amplitudę napięcia Um znamy, przesunięcie fazowe obliczyliśmy.
\[ u(t)=U_m \sin(\omega t + \varphi_{0u})=U_m \ sin( 2 \pi f t + \varphi_{0u} ) \]
\[u(t)\,\dot {=}\,100 \cdot \sin( 2 \pi 50 t + \frac{\pi}{4} )\,\mathrm V = 100\cdot \ sin( 100 \pi t + \frac{\pi}{4} )\,\mathrm V\]
Do powyższej relacji podstawiamy czas wyrażony w sekundach.
Odpowiedź
Równania chwilowych wartości napięcia i natężenia prądu przemiennego w obwodzie RLC:
\[ i(t)=0{,}79 \cdot \sin(100 \pi t)\,\mathrm A\]
\[u(t)=100 \cdot \sin( 100 \pi t + \frac{\pi}{4} )\,\mathrm V \]



