Dwie kulki zawieszone na nici
Kod zadania: 734
Podpowiedź
Jakie siły działają na kulki i jaki jest ich zwrot? Spróbuj narysować działające siły.Rozkład sił działających na kulki
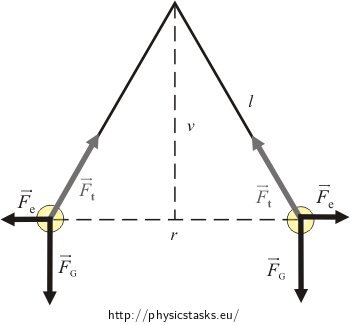
Analiza
Na każdą kulkę zawieszoną na nici działa siła grawitacji oraz siła naciągu nici. Nasze kulki są naładowane (naelektryzowane) działa więc na nie także odpychająca siła elektrostatyczna. Obie kulki są w stanie spoczynku, ponieważ wypadkowa wszystkich trzech sił musi być równa zero. Wypadkowa wartość siły grawitacji i oddziaływania elektrostatycznego jest co do wartości równa sile naciągu nici, ale ma przeciwny do niej zwrot. Na zdjęciu można znaleźć dwa trójkąty podobne (zielony i fioletowy). Z podobieństwa obu trójkątów można wyznaczyć nieznaną wartość siły elektrycznej i ładunek kulek.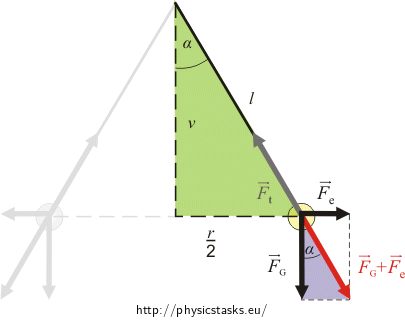
Rozwiązanie
Na każdą kulkę zawieszoną na nici działa siła grawitacji \( \vec{F}_G\) i siła naciągu włókna \( \vec{F}_t\). Ponieważ kulki naładowane są tym samym ładunkiem (o tym samym znaku), musi pojawić się dodatkowa siła odpychania elektrostatycznego \( \vec{F}_e\).
Wartość siły oddziaływania elektrostatycznego można określić na podstawie prawa Coulomba:
\[F_e \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q_1 Q_2}{r^2}.\]Obie kulki są naładowane jednakowym ładunkiem Q, możemy więc zapisać: \[F_e \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q^2}{r^2}.\]
Ponieważ kule są w spoczynku wypadkowa wszystkich trzech sił musi być równa zero.
Wypadkowa sił \(\vec{F}_e+\vec{F}_G\) przeciwdziałać sile naciągu włókna \(\vec{F}_t\). Dzięki temu zaznaczone na zielono i fioletowo trójkąty są do siebie podobne. Z "fioletowego trójkąta" otrzymujemy tg α.
\[\mathrm{tg}\,{\alpha}\,=\,\frac{F_e}{F_G}\,=\,\frac{\frac{1}{4\pi\varepsilon_0}\,\frac{Q^2}{r^2}}{mg}\,=\,\frac{Q^2}{4 \pi\varepsilon_0mgr^2}\]Kąt α znajdziemy także w "zielonym trójkącie". Wyraźmy ponownie ten kąt.
\[\mathrm{tg}\,{\alpha}\,=\,\frac{\frac{r}{2}}{v}\,=\,\frac{r}{2v}\]Długość v w "zielonym trójkącie" obliczamy z Twierdzenia Pitagorasa: \(v\,=\,\sqrt{ l^2-(\frac{r}{2})^2}\) i podstawiamy
\[\mathrm{tg}{\alpha}\,=\,\frac{r}{2 \sqrt{ l^2-(\frac{r}{2})^2} }\,=\,\frac{r}{ \sqrt{ 4l^2-r^2} }.\]Przyrównujemy oba równania na tangens kąta α
\[\frac{Q^2}{4 \pi \varepsilon_0 mgr^2}\,=\,\frac{r}{\sqrt{ 4l^2-r^2} } \]i wyznaczmamy z niego nieznaną wartość ładunku Q:
\[Q^2\,=\,\frac{4 \pi \varepsilon_0 mgr^3}{\sqrt{ 4l^2-r^2} } \] \[Q\,=\,\sqrt{\frac{4 \pi \varepsilon_0 mgr^3}{\sqrt{ 4l^2-r^2} } }.\]Wartości liczbowe
\[m\,=\,0{,}5\,\mathrm{g}\,=\,5\cdot {10^{-4}}\,\mathrm{kg}\] \[l\,=\,1\,\mathrm{m}\] \[r\,=\,4\,\mathrm{cm}\,=\,4\cdot {10^{-2}}\,\mathrm{m}\] \[Q\,=\,?\,\left(\mathrm{C}\right)\]Stałe odczytujemy z tablic fizycznych:
\[\varepsilon_0\,=\,8{,}85\cdot {10^{-12}}\,\mathrm{ C^2\,N^{-1}\,m^{-2}}\] \[g\,=\,9{,}8\,\mathrm{ m\,s^{-2}}\]
\[Q\,=\,\sqrt{\frac{4 \pi \varepsilon_0 mgr^3}{\sqrt{ 4l^2-r^2} } }\] \[ Q\,=\,\sqrt{\frac{4\pi \,\cdot\,8{,}85\cdot {10^{-12}}\, \cdot \,5\cdot {10^{-4}}\, \cdot\,9{,}8 \,\cdot\, \left(4 \cdot{10^{-2}}\right)^3}{ \sqrt{ 4 \cdot {1^2}-\left(4 \cdot{10^{-2}}\right)^2}}}\,\mathrm{C}\] \[Q\,\dot=\,4{,}2\cdot{10^{-9}}\,\mathrm{C}\,\dot=\,4{,}2\,\mathrm{nC} \]Odpowiedź
Każda kulka naładowana jest ładunkiem o wartości: \[Q\,=\,\sqrt{\frac{4 \pi \varepsilon_0 mgr^3}{\sqrt{ 4l^2-r^2} }} \,\dot=\,4{,}2\,\mathrm{nC} \] .




