Ramka i przewód z prądem
Kod zadania: 732
Metalowa ramka o szerokości a = 5 cm i wysokości b = 10 cm oddala się z prędkością 4m/s od prostoliniowego przewodu, przez który płynie prąd o natężeniu 3 A. Wektor prędkości jest prostopadły do przewodu tak, jak pokazuje poniższy rysunek. Ramka w trakcie ruchu pozostaje w tej samej płaszczyźnie. Wyznacz wartość indukowanego napięcia, jeśli początkowa odległość między ramką i przewodem wynosi d = 2 cm.
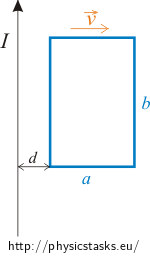
Podpowiedź
Zastanów się nad równaniem opisującym napięcie indukowane w ramce. Jaki jest strumień magnetyczny przechodzący przez ramkę?Analiza
Napięcie indukowane w ramce jest równe zmianie w jednostce czasu strumienia magnetycznego (ze znakiem minus) przechodzącego przez ramkę. Zmiana strumienia magnetycznego jest równa różnicy między początkowym i końcowym strumieniem magnetycznym. Dla zadanego przedziału czasowego dt wyraźmy początkowy i końcowy strumień objęty przez ramkę jako Φ1 i Φ2, odpowiednio, a przez Φ’ różnicę między tymi dwoma strumieniami Φ’ = Φ1 - Φ2.Rysunek
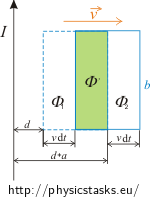
UWAGA: Przemieszczenie ramki traktujemy jako nieskończenie małe. Aby rysunek był bardziej czytelny, przesunięcie pokazano jako znacznie większe.
Rozwiązanie
Napięcie indukowane w ramce jest, w myśl ogólnego wzoru, równe zmianie strumienia przez powierzchnię ramki w jednostce czasu
\[U_i=-\frac{\mathrm{d} \Phi}{\mathrm{d}t},\]gdzie dΦ jest zmianą strumienia magnetycznego w czasie dt i może być zastąpione różnicą między początkowym i końcowym strumieniem magnetycznym
\[\mathrm{d}\Phi = \Phi_1 -\Phi_2.\]Strumień obejmowany przez ramkę w dwóch różnych momentach czasu odległych o dt można wyrazić jako sumę strumienia magnetycznego Φ,, który jest wspólną częścią Φ1 i Φ2, oraz zmian dΦ1 i dΦ2.
\[\Phi_1 = \Phi^, + \mathrm{d}\Phi_{1}\] \[\Phi_2 = \Phi^, + \mathrm{d}\Phi_{2}\]Gdy policzymy zmianę strumienia magnetycznego dΦ (równanie 2), to wtedy strumień Φ’ zniknie. Musimy tylko wyznaczyć strumień magnetyczny dΦ1 i dΦ2. Ponieważ obszar, w którym mierzymy strumień magnetyczny, jest mały w porównaniu do długości drutu, pole magnetyczne B(r) w określonej odległości r od drutu traktujemy jako stałe. Dlatego też możemy skorzystać z ogólnego wzoru na strumień magnetyczny:
\[\Phi =BS\cos{\alpha},\]gdzie α jest kątem między normalną do powierzchni i liniami pola magnetycznego. W rozważanym przypadku α = 0°, więc cos α = 1. Indukcję pola magnetycznego B można zapisać korzystając z równania opisującego indukcję pola magnetycznego wokół długiego prostoliniowego przewodu
\[B=\frac{\mu_o}{2\pi}\frac{I}{d}\]Uwzględniamy pole powierzchni S, w którym mierzymy strumień magnetyczny. W naszym przypadku zmiany dΦ1 i dΦ2 dotyczą takiej samej zmiany powierzchni (spójrz na rysunek).
\[S = b v dt\]Przekształcamy równania na Φ1 i Φ2 (używając równań 5 -7):
\[\Phi_1 = \Phi^, + \,\frac{\mu_o}{2\pi}\frac{I}{d}\,b\,v\,\mathrm{d}t\] \[\Phi_2 = \Phi^, + \,\frac{\mu_o}{2\pi}\frac{I}{d+a}\,b\,v\,\mathrm{d}t.\]Równanie opisujące zmianę strumienia magnetycznego będzie miało postać [korzystamy z (2), (8), (9)]
\[\mathrm{d}\Phi = \frac{\mu_o Ibvdt}{2\pi} (\frac{1}{d}-\frac {1}{d+a})\]Zapiszemy napięcie indukowane korzystając z równań (1) i (10):
\[U_i = \frac{\mu_o Ibvdt}{2\pi dt} (\frac{1}{d}-\frac {1}{d+a}).\]Po matematycznych uproszczeniach otrzymujemy:
\[U_i = \frac{\mu_o Ibv}{2\pi}\, \frac{a}{d(d+a)}.\]Rozwiązanie liczbowe
\[v=4 \,\mathrm{ms^{-1}}\] \[a = 5\,\mathrm{cm}=0{,}05 \,\mathrm{m}\] \[b=10\,\mathrm{cm}=0{,}10 \,\mathrm{m} \] \[d = 2\,\mathrm{cm}=0{,}02 \,\mathrm{m}\] \[I = 3\,\mathrm{A}\] \[U_i = \mathrm{?}\]
\[|U_i| = \frac{\mu_o Ibv}{2\pi}\, \frac{a}{d(d+a)}= \frac{4\cdot \pi \cdot 10^{-7} \cdot3\cdot{0{,}1}\cdot 4}{2\pi}\,\cdot \frac{0{,}05}{0{,}02\cdot(0{,}02+0{,}05)}\,\mathrm{V}\] \[|U_i|=8{,}6\,\mathrm{\mu V}\]Odpowiedź
Wartość indukowanego napięcia wynosi 8,6 mikrowoltów.



