Dwie kulki zawieszone na nici umieszczone w benzenie
Kod zadania: 539
Dwie kulki obdarzone takim samym ładunkiem elektrycznym są zawieszone na niciach o identycznej długości. Kulki odpychają się tak, że w punkcie zawieszenia nici między nimi powstaje kąt 2α.
Wyznacz gęstość materiału, z którego wykonane są kulki, jeśli po ich zanurzeniu w benzenie kąt rozchylenia nici nie zmienia się.
Uwaga: Gęstość benzenu ρb = 879 kg m−3, a stała dielektryczna (przenikalność dielektryczna względna) εr = 2,3.
Podpowiedź 1
Jakie siły działają na kulki? Jaki warunek musi być spełniony?
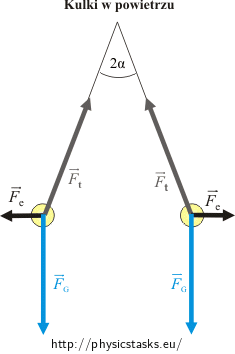
Wykonaj rysunek pomocniczy, zaznacz na nim siły działające na kulki w powietrzu.
Podpowiedź 2
Które siły zmienią się po zanurzeniu kulek w benzenie? Czy po zanurzeniu zaczną działać jakieś inne siły?
Rysunki
Analiza
W powietrzu na każdą kulkę działają trzy siły: ciężar, siłą naciągu nici, siła odpychania kulombowskiego. Kulki pozostają w spoczynku tak długo, dopóki wypadkowa siła jest równa zero.
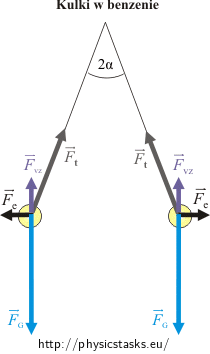
Po zanurzeniu kulek w benzenie niektóre siły zmieniają się, ale nadal wypadkowa siła musi być równa zero.
Siła odpychania kulombowskiego będzie εr razy mniejsza, a siła naciągu nici również się zmieni. Siła ciężkości nie zmieni się. Natomiast zacznie działać nowa siła – siła wyporu.
W każdym przypadku można wyrazić funkcję tangens kąta α korzystając z trójkąta prostokątnego. Porównując oba wyrażenia można wyznaczyć nieznaną gęstość.
Rozwiązanie
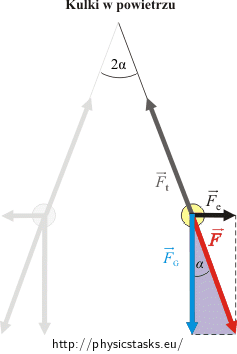
Siły ciężkości \(\vec{F}_G\) i naciągu nici \(\vec{F}_t\) działają na kulki w powietrzu. Naelektryzowane kulki odpychają się siłą Coulomba \(\vec{F}_e\).
Można zapisać wzory opisujące wartości sił:
\[F_G\,=\,mg\] \[F_e\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{Q^2}{r^2}\,,\]gdzie r to odległość między kulkami.
Kulki pozostają w spoczynku dopóki siła wypadkowa (z tych trzech sił) jest równa zero.
Można zapisać funkcję tangens kąta α korzystając z trójkąta prostokątnego - fioletowego.
\[\mathrm{tg} {\alpha}=\frac{F_e}{F_G}\,=\,\frac{\frac{1}{4 \pi \varepsilon_0}\, \frac{Q^2}{r^2}}{mg}\] \[\mathrm{tg} {\alpha}\,=\,\frac{1}{4 \pi \varepsilon_0} \,\frac{Q^2}{mgr^2}\tag{*}\]Jeśli kulki są zanurzone w benzenie zaczyna działać nowa siła - siła wyporu: \(\vec{F}_{VZ}\). Siła ciężkości nie zmienia się, ale siła odpychania kulombowskiego jest εr razy mniejsza. Siła naciągu także ulega zmianie.
\[F_G\,=\,mg\] \[F_e\,=\,\frac{1}{4 \pi \varepsilon_0 \varepsilon_r}\, \frac{Q^2}{r^2} \] \[F_{VZ}\,=\,V \varrho_b g\]Siła wypadkowa tych trzech sił musi być równa zero.
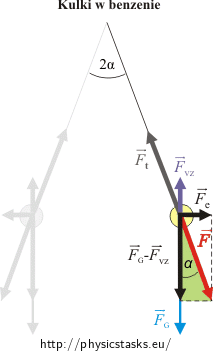
Tym razem funkcję tangens kąta α, zapiszemy korzystając z trójkąta prostokątnego - zielonego:
\[\mathrm{tg} {\alpha}\,=\,\frac{F_e}{F_G-F_{VZ}}\,=\,\frac{\frac{1}{4 \pi \varepsilon_0 \varepsilon_r}\, \frac{Q^2}{r^2}}{mg-V \varrho_b g} \] \[\mathrm{tg} {\alpha}\,=\,\frac{1}{4 \pi \varepsilon_0 \varepsilon_r}\, \frac{Q^2}{r^2\left(mg-V \varrho_b g \right)}.\tag{**}\]Teraz należy przyrównać równania (*) i (**)
\[\frac{1}{4 \pi \varepsilon_0} \,\frac{Q^2}{mgr^2} \,=\,\frac{1}{4 \pi \varepsilon_0 \varepsilon_r}\, \frac{Q^2}{r^2g\left(m-V \varrho_b \right)}\]Następnie obie strony otrzymanego równania pomnożyć przez \(4 \pi \varepsilon_0 gr^2\) i podzielić przez Q2, dostaniemy wówczas równość:
\[\frac{1}{m} \,=\,\frac{1}{ \varepsilon_r}\, \frac{1}{m-V \varrho_b }.\]Za masę kulki można podstawić zależność: m = V ρ i równanie będzie miało postać:
\[\frac{1}{V\varrho}\, =\,\frac{1}{ \varepsilon_r}\, \frac{1}{V\varrho-V \varrho_b }.\]Z powyższego równania można wyznaczyć szukaną gęstość:
\[\frac{1}{\varrho}\,=\,\frac{1}{ \varepsilon_r}\, \frac{1}{\varrho-\varrho_b }\] \[\varrho\,=\,\varepsilon_r \left(\varrho-\varrho_b \right).\]Opuszczamy nawias i przenosimy na lewą stronę równości szukaną gęstość:
\[\varepsilon_r \varrho-\varrho\,=\,\varepsilon_r \varrho_b\] \[\varrho \left(\varepsilon_r -1\right)\,=\,\varepsilon_r \varrho_b\] \[\varrho\,=\,\frac{\varrho_b \varepsilon_r }{\varepsilon_r -1}.\]Wartości liczbowe
ρb = 879 kg m-3 - gęstość benzenu
εr = 2,3
ρ = ? ( kg m-3)
\[\varrho\,=\,\frac{\varrho_b \varepsilon_r }{\varepsilon_r -1}\,=\,\frac{2{,}3 \,\cdot\, 879}{2{,}3-1}\,\mathrm{kg\,m^{-3}}\,\dot{=}\,1 600\,\mathrm{kg\,m^{-3}}\]Korzystając z tablic stałych fizycznych dowiesz się, że materiałem, z którego są zrobione kulki, jest pewien rodzaj tworzywa sztucznego.
Odpowiedź
Kulki są wykonane z materiału o gęstości \(\varrho=\frac{\varrho_b \varepsilon_r }{\varepsilon_r -1}\dot{=}\,1\,600\,\mathrm{kg\,m^{-3}}\).




