Opór sześcianu

Kod zadania: 543

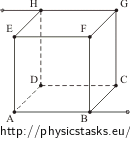
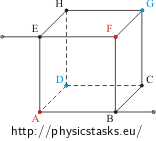
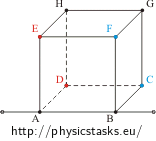
Znajdź opór między dwoma wierzchołkami sześcianu wykonanego z przewodnika:

a) między wierzchołkami H i B leżącymi na przekątnej sześcianu	b) między wierzchołkami E i B leżącymi na przekątnej przedniej ściany	c) między wierzchołkami A i B leżącymi na jednej krawędzi sześcianu

Opór każdej krawędzi jest równy R.

Podpowiedź 1
Co się dzieje, jeśli połączymy punkty o tym samym potencjale?

Które z punktów mają taki sam potencjał?
Podpowiedź 2
Narysuj obwód na płaszczyźnie łącząc punkty o tym samym potencjale.
Analiza
Napięcie między opornikami jest równe różnicy potencjału między końcami oporników. Potencjał w punkcie A ma pewną podaną wartość. Nasz obwód rozgałęzia się w tym punkcie. Dzięki symetrii sześcianu wiemy, że natężenia prądu płynącego przez niektóre "oczka" (które zaczynają się w punkcie A) są takie same. Dlatego też napięcia również są takie same (ponieważ ich opór jest identyczny), a potencjał na końcach tych krawędzi jest taki sam (zmiana potencjału z punktu A jest także jednakowa).

Możemy połączyć punkty o równym potencjale w jednym węźle, miedzy tymi punktami nie będzie przepływał żaden prąd (ten sam potencjał = to samo napięcie). Te zmiany w obwodzie nie zmienią ani wartości ani oporu zastępczego (całkowitego) obwodu.

Znajdź punkty o tym samym potencjale i złącz je w jednym węźle. Następnie narysuj obwód na płaszczyźnie i dołącz do każdej części przewodu opornik o oporze R.

Korzystając z reguł obliczania oporu zastępczego oporników połączonych równolegle i szeregowo wyznacz opór całkowity sześcianu.
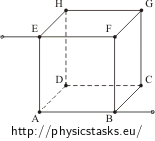
Rozwiązanie części a): opór między wierzchołkami H i B leżącymi na przekątnej sześcianu

W tym obwodzie krawędzie BA, BC i BF są równe, natężenie prądu jest takie samo. Ponadto punkty: A, C i F mają taki sam potencjał. Opór całego sześcianu nie zmienia się przez połączenie punktów w jeden.

Taka sama sytuacja dotyczy punktów D, E, G.

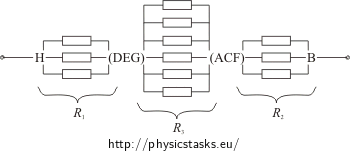
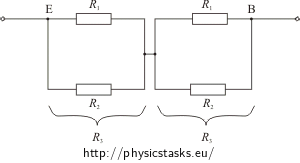
Połączmy punkty A, C i F w jednym węźle (D, E i F w następnym), przerysujmy obwód na płaszczyźnie i dodajmy na krawędziach oporniki, każdy o oporze R.

Opory: R₁ między punktem H i punktami (DEG), R₂ między punktami (ACF) i punktem B są równe oporowi trzech oporników połączonych równolegle.
\[\frac{1}{R_1}\,=\,\frac{1}{R_2}\,=\,\frac{1}{R}+\frac{1}{R}+\frac{1}{R}\] \[R_1\,=\,R_2\,=\,\frac{R}{3}\]
Opór R₃ w węźle między (DEG) i (ACF) jest równy oporowi zastępczemu sześciu oporników połączonych równolegle.
\[\frac{1}{R_3}\,=\,\frac{6}{R}\] \[R_3\,=\,\frac{R}{6}\]
Opory R₁, R₂, R₃ są połączone szeregowo. Opór całkowity sześcianu między punktami H i B jest równy:
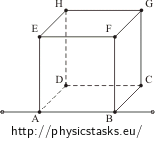
\[R_{HB}\,=\,R_1+R_2+R_3\,=\,2\frac{R}{3}+\frac{R}{6}\] \[R_{HB}\,=\,\frac{5}{6}R.\]
Rozwiązanie części b): opór między wierzchołkami E i B leżącymi na przekątnej przedniej ściany

W takim obwodzie punkty A i F (D i G) mają ten sam potencjał. Opór sześcianu nie zmienia się przez połączenie tych punktów.

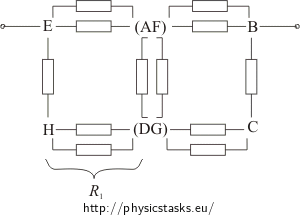
Połączmy punkty A i F (D i G) w jedno "oczko", przerysujmy obwód na płaszczyźnie i dorysujmy oporniki na każdej krawędzi. Każdy opornik ma opór R.

Połączmy każde oczko posiadające dwa oporniki R połączone równolegle w jeden o oporze R₁ wówczas:
\[\frac{1}{R_1}\,=\,\frac{1}{R}+\frac{1}{R}\] \[R_1\,=\,\frac{R}{2}.\]
Uproszczony schemat obwodu:

Korzystając z symetrii obwodu zauważmy, że nie ma żadnego prądu płynącego między punktami (AF) i (DG). Punkty (AF) i (DG) mają taki sam potencjał. Można więc pominąć ten opór w dalszych obliczeniach.

Rozważmy każde oczko zawierające oporniki R połączone szeregowo jako opór R₂:
\[R_2\,=\,R_1+R\,=\,\frac{R}{2}+R\,=\,\frac{3}{2}R.\]
Przerysujmy obwód raz jeszcze:

Mamy teraz obwód składający się z dwóch oporników R₃ połączonych szeregowo. Każdy z oporników R₃ składa się z oporników R₁ i R₂ połączonych równolegle.

Pamiętając, że: \(R_1\,=\,\frac{R}{2}\), \(\hspace{10px} R_2\,=\,\frac{3}{2}R\),

wyznaczamy opór R₃:
\[\frac{1}{R_3}\,=\,\frac{1}{R_1}+\frac{1}{R_2}\,=\,\frac{R_1+R_2}{R_1R_2} \] \[\frac{1}{R_3}\,=\,\frac{\frac{R}{2}+\frac{3}{2}R}{\frac{R}{2}\cdot \frac{3}{2}R} \,=\,\frac{\frac{4}{2}R}{\frac{3}{4}R^2}\,=\,\frac{2}{\frac{3}{4}R}\,=\,\frac{8}{3R}\] \[R_3\,=\,\frac{3}{8}R.\]
Opór zastępczy między punktami E i B jest równy:
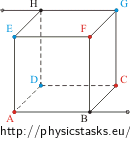
\[R_{EB}\,=\,R_3+R_3\,=\,2R_3\,=\,2\frac{3}{8}R\] \[R_{EB}\,=\,\frac{3}{4}R.\]
Rozwiązanie części c): opór między wierzchołkami A i B leżącymi na jednej krawędzi sześcianu

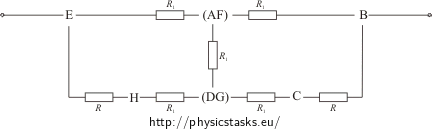
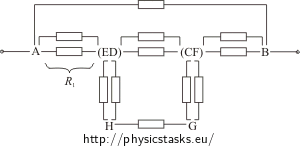
W tym obwodzie punkty E i D (F i C) mają taki sam potencjał. Opór całego sześcianu nie zmienia się przez połączenie tych punktów. Połączmy punkty E i D (F i C) w jedno oczko, przerysujmy schemat na płaszczyźnie i dodajmy oporniki na krawędziach. Opór każdego z nich jest równy R.

Rozważmy każde oczko zawierające dwa oporniki połączone równolegle, połączmy je w jeden opornik o oporze R₁:
\[\frac{1}{R_1}\,=\,\frac{1}{R}+\frac{1}{R}\] \[R_1\,=\,\frac{R}{2}.\]
Uproszczony schemat obwodu:

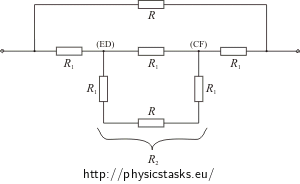
Opór R₂ między oczkami (ED) oraz (CF) jest równy:
\[\frac{1}{R_2}\,=\,\frac{1}{R_1}+\frac{1}{\left(R_1+R+R_1\right)}\] \[\frac{1}{R_2}\,=\,\frac{1}{\frac{R}{2}}+\frac{1}{2\frac{R}{2}+R}\,=\,\frac{2}{R}+\frac{1}{2R}\,=\,\frac{5}{2R}\] \[R_2\,=\,\frac{2}{5}R.\]
Opór całego sześcianu jest równy:
\[\frac{1}{R_{AB}}\,=\,\frac{1}{R}+\frac{1}{R_1+R_2+R_1}.\]
Podstawiamy \(R_1\,=\,\frac{R}{2},\) \(R_2\,=\,\frac{2}{5}R,\) aby obliczyć R_AB
\[ \frac{1}{R_{AB}}\,=\,\frac{1}{R}+\frac{1}{2\frac{R}{2}+\frac{2}{5}R}\,=\, \frac{1}{R}+\frac{1}{R+\frac{2}{5}R}\,=\,\frac{1}{R}+\frac{1}{\frac{7}{5}R} \] \[\frac{1}{R_{AB}}\,=\,\frac{1}{R}+\frac{5}{7R}\,=\,\frac{12}{7R}.\]
Opór zastępczy między punktami A i B jest równy:
\[R_{AB}\,=\,\frac{7}{12}R.\]
Odpowiedź
Całkowity opór między punktami H i B jest równy \(\frac{5}{6}R\).

Całkowity opór między punktami E i B jest równy \(\frac{3}{4}R\).

Całkowity opór między punktami A i B jest równy \(\frac{7}{12}R\).