Indukcyjność cewki rotującej w polu magnetycznym
Kod zadania: 1012
Cewka w kształcie walca o długości 10 cm i liczbie zwojów 600 oraz promieniu 2 cm rotuje w polu magnetycznym o indukcji 3·10-3 T. Określ:
a) maksymalny strumień indukcji magnetycznej we wnętrzu cewki,
b) indukcyjność cewki.
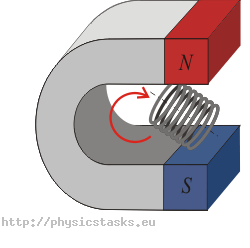
Podpowiedź a) Maksymalna wartość strumienia indukcji magnetycznej
Strumień indukcji magnetycznej obejmowany przez cewkę będzie największy, kiedy przez jej przekrój poprzeczny przechodzić będzie największa liczba linii.
Zastanów się, jak w stosunku do wektora zewnętrznego pola magnetycznego powinna być położona cewka, aby strumień indukcji magnetycznej był największy.
Podpowiedź b) Co to jest indukcyjność cewki
Indukcyjność cewki to wielkość skalarna, charakteryzująca zjawisko indukcji w podłączonym do źródła prądu przewodniku, np. w cewce. Przewodnik, przez który przepływa prąd o natężeniu I, wytwarza wokół siebie pole magnetyczne, dla którego możemy określić strumień indukcji magnetycznej Φ. Indukcyjność przewodnika określa wyrażenie
\[L=\frac{\Phi}{I}.\]Pole magnetyczne określone jest przez natężenie prądu płynącego w przewodniku, zaś strumień indukcji magnetycznej zależy od natężenia pola magnetycznego, co oznacza, że indukcyjność nie zależy od natężenia płynącego prądu. Jej wartość określona jest przez parametry przewodnika.
Jednostką indukcyjności jest henr – symbol H.
Analiza
Maksymalny strumień indukcji magnetycznej
Strumień indukcji magnetycznej dla cewki będzie największy, gdy przez jej zwoje będzie przechodzić „najwięcej“ linii pola magnetycznego. Będzie tak w przypadku, gdy wektor pola magnetycznego ustawi się prostopadle do płaszczyzny przekroju cewki.Indukcyjność cewki
Ponieważ cewka rotuje w polu magnetycznym, zmienia się strumień indukcji magnetycznej i w cewce indukuje się prąd zmienny. Gdy tylko przez cewkę popłynie prąd, wokół niej pojawi się pole magnetyczne. Strumień indukcji magnetycznej tego pola jest proporcjonalny do indukowanego prądu. Współczynnik proporcjonalności pomiędzy strumieniem indukcji magnetycznej cewki a wartością indukowanego prądu, określamy jako indukcyjność cewki.
Rozwiązanie a) Maksymalny strumień indukcji magnetycznej
Określmy wyrażenie na maksymalny strumień indukcji magnetycznej dla cewki. Ponieważ pole magnetyczne, w którym znajduje się cewka, możemy uważać za jednorodne, strumień indukcji magnetycznej Φ cewki dany jest wzorem
\[\Phi=NBS\cos\alpha,\]gdzie α to kąt między wektorem indukcji magnetycznej \(\vec{B}\) a wektorem prostopadłym do powierzchni \(\vec{S}.\)
Strumień indukcji magnetycznej będzie maksymalny, gdy cos α = 1, tj. α = 0°. Wektory \(\vec{B}\) i \(\vec{S}\)w takim przypadku będą równoległe. To oznacza, że wektor indukcji magnetycznej \(\vec{B}\) jest prostopadły do płaszczyzny przekroju S. Maksymalny strumień indukcji magnetycznej ma zatem postać
\[\Phi_{max}=NBS.\]Pole powierzchni przekroju cewki S równe jest polu koła o promieniu r.
Na maksymalny strumień indukcji magnetycznej Φmax dostajemy więc
\[\Phi_{max}=\pi r^2 NB.\]Rozwiązanie b) Indukcyjność cewki
Rotująca cewka znajduje się w polu magnetycznym i dzięki temu indukuje się w niej napięcie. Jeśli cewka jest podłączona, będzie w niej płynął prąd. Z kolei prąd wytworzy swoje własne pole magnetyczne, nazwijmy je polem cewki. Indukcyjność L to współczynnik proporcjonalności między chwilowym strumieniem indukcji pola magnetycznego cewki Φ a chwilowym natężeniem prądu i, płynącego przez cewkę, tj.
\[\Phi(t)=Li(t).\tag{1}\]Będziemy roważać położenie, w którym strumień indukcji magnetycznej jest największy. W poprzednim podpunkcie pokazaliśmy, że będzie tak w przypadku, gdy wektor indukcji magnetycznej jest prostopadły do powierzchni przekroju poprzecznego cewki.
Dla strumienia indukcji magnetycznej
\[\Phi=NBS.\]Na wartość indukcji magnetycznej podstawimy wyrażenie dla wnętrza długiej cewki
\[B=\mu_o\frac{N}{l}i.\]Wyrażenia te podstawimy do równania (1)
\[NBS=Li,\] \[N\mu_o\frac{N}{l}iS=Li\]i obliczymy indukcyjność cewki L
\[L=\mu_o\frac{N^2S}{l}.\]Zapis danych i rozwiązanie liczbowe
\[l\,=\,10\,\mathrm{cm}=\,0{,}10\,\mathrm{m}\] \[r\,=\,2\,\mathrm{cm}=\,0{,}02\,\mathrm{m}\] \[B\,=\,3\cdot{10^{-3}}\,\mathrm{T}\] \[N\,=\,600\] \[\Phi\,= \,?\] \[L\,= \,?\]Z tablic
\[\mu_o\,= \,4\pi\cdot{10^{-7}}\,\mathrm{Hm^{-1}}\]
\[\Phi_{max}=\pi r^2 NB=\pi\cdot{0{,}02^2}\cdot{600}\cdot {3}\cdot{10^{-3}}\,\mathrm{Wb}\,\dot{=}\,2\cdot{10^{-3}}\,\mathrm{Wb}\] \[L=\mu_o\pi\,\frac{(Nr)^2}{l}=4\cdot\pi^2\cdot{10^{-7}}\cdot\frac{(600\cdot{0{,}02})^2}{0{,}10}\,\mathrm{H}\,\dot{=}\,6\cdot{10^{-3}}\,\mathrm{H}\]Odpowiedź
Maksymalny strumień indukcji magnetycznej dla rozważanej cewki ma wartość w przybliżeniu równą Φ = 2 mWb.
Cewka ma indukcyjność około L = 6 mH.



