Czajnik w ogrodzie
Kod zadania: 541
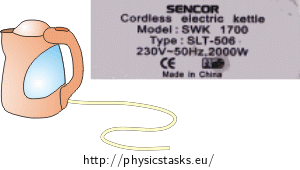
Czajnik elektryczny stojący w ogrodzie jest podłączony do napięcia 230 V przez przewód o długości 60 m i oporze 1,2 Ω. Oto dane dotyczące czajnika:
a) Znajdź napięcie prądu płynącego przez grzałkę i moc.
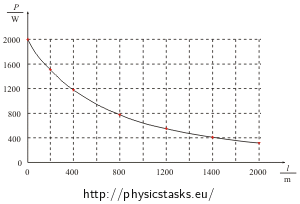
b) Mając dany przekrój poprzeczny kabla narysuj zależność mocy czajnika od długości kabla w zakresie od 0 do 2 000 m.
Komentarz
Korzystamy ze średniej kwadratowej wartości napięcia i natężenia prądu, dlatego możemy poradzić sobie z zadaniem zakładając, że czajnik jest podłączony do obwodu prądu stałego.
Podpowiedź
Na tabliczce informacyjnej czajnika podane są wartości napięcia i częstotliwości na wejściu. Są to wartości charakterystyczne dla czajnika.
Korzystamy ze średniej kwadratowej i rozważamy tylko opór czajnika, nie jest nam potrzebna częstotliwość prądu przemiennego.
Analiza
a) Chwilowe napięcie prądu płynącego przez grzałkę czajnika i jego moc
Moc jest iloczynem napięcia i natężenia prądu płynącego przez urządzenie. Natężenie jest równe ilorazowi napięcia i oporu. Dane zapisane na tabliczce informacyjnej wyznaczają więc parametry czajnika, które pozwalają na obliczenie oporu czajnika z podanym napięciem i natężeniem.
Rozważmy kabel i czajnik jako dwa oporniki połączone szeregowo, natężenie prądu przez nie płynącego jest takie samo. Aby wyznaczyć natężenie, wstawimy wartość napięcia pochodzącego ze źródła (np. 230 V w domowej instalacji) oraz całkowity opór dwóch oporników do prawa Ohma. Chwilowe napięcie prądu płynącego przez czajnik jest proporcjonalne do natężenia i oporu.
Znając natężenie i napięcie prądu płynącego przez czajnik, możemy znaleźć moc.
b) Zależność prądu wejściowego od długości przewodu - kabla
Opór przewodnika (wykonanego z metalu) jest proporcjonalny do jego długości i odwrotnie proporcjonalny do pola powierzchni przekroju poprzecznego. Zależy także od oporu właściwego materiału, z którego wykonano przewód (od rodzaju materiału).
Pole przekroju poprzecznego i opór właściwy nie ulegają zamianie pod warunkiem, że długość przewodnika nie zmienia się. Znając opór przewodu przy określonej długości możemy wyznaczyć opór właściwy dzieląc przez siebie te dane. Iloraz ten wstawiamy do równania na opór przewodu w funkcji długości.
Aby znaleźć zależność prądu wejściowego od długości przewodu skorzystamy z równania otrzymanego w części a) i zastąpimy opór przewodu równaniem opisującym opór w funkcji długości przewodu.
Rozwiązanie części a): Napięcie chwilowe prądu przepływającego przez grzałkę czajnika
Rozważmy przewód i czajnik jako dwa oporniki połączone szeregowo. Niech R0 oznacza opór przewodu, a R opór czajnika elektrycznego (grzałki czajnika).
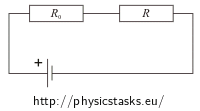
Korzystamy z prawa Ohma do wyznaczenia natężenia prądu:
\[I\,=\,\frac{U_0}{R_0+R}\]gdzie U0 odpowiada napięciu.
Rozważmy przewód i czajnik jako dwa oporniki połączone szeregowo, stąd natężenie prądu w obwodzie można zapisać jako:
\[I\,=\,\frac{U}{R}\]Porównujemy oba równania:
\[\frac{U_0}{R_0+R}\,=\,\frac{U}{R}\]i możemy teraz wyrazić chwilowe napięcie prądu płynącego przez grzałkę:
\[U\,=\,\frac{U_0R}{R_0+R}\tag{*}\]Z tabliczki informacyjnej czajnika odczytujemy wartości 230 V i 2 000 W. Informują one, że po podłączeniu czajnika do źródła Us = 230 V jego moc będzie równa Ps = 2 000 W. Korzystając z tych danych obliczymy opór czajnika R.
Moc czajnika jest dana wzorem:
\[P_s\,=\,U_sI\,=\,\frac{U_s^2}{R}\]gdzie Us oznacza napięcie prądu płynącego przez grzałkę, a R to opór grzałki.
Wyznaczymy opór i wstawimy dane z tabeli. Otrzymujemy opór grzałki:
\[R\,=\,\frac{U_s^2}{P_s}\]Powyższą zależność wstawiamy do równania (*):
\[U\,=\,\frac{U_0\frac{U_s^2}{P_s}}{R_0+\frac{U_s^2}{P_s}}\,=\,\frac{U_0U_s^2}{P_s\left(R_0+\frac{U_s^2}{P_s}\right)}\]i podstawimy chwilowe napięcie prądu przepływającego przez grzałkę czajnika:
\[U\,=\,\frac{U_0U_s^2}{P_sR_0+U_s^2}.\]Teraz można wstawić następujące wartości: U0 = 230 V, R0 = 1,2 Ω, Ps = 2 000 W, Us = 230 V
\[U\,=\,\frac{230^3}{2\,000\cdot{1{,}2}+230^2}\,\mathrm{V}\,=\,220\,\mathrm{V}\]Rozwiązanie części b): Zależność mocy od długości przewodu
Korzystając z poprzedniej części rozwiązania można zapisać następujący wzór na moc:
\[P\,=\,\frac{U_0^2U_s^2P_s}{\left(P_sR_0+U_s^2\right)^2}\tag{*}\]Opór przewodu zmienia się wraz z długością - opór przewodnika jest wprost proporcjonalny do jego długości:
\[R\,=\,\rho\frac{l}{S}\]gdzie ρ – opór właściwy (zależny od rodzaju materiału), l – długość, S – pole przekroju poprzecznego przewodu.
Stosunek oporu właściwego i przekroju poprzecznego jest stały, stąd stosunek oporu przewodu i długości l0:
\[R_0\,=\,\rho\frac{l_0}{S}\hspace{10px}\Rightarrow\hspace{10px}\frac{\rho}{S}\,=\,\frac{R_0}{l_0}\]Możemy wyliczyć opór przewodnika z równania:
\[R\,=\,\frac{l}{l_0}R_0\]Jeśli chcemy zbadać zależność mocy grzałki od długości przewodu, musimy umieścić R0 w równaniu (*) zamiast oporu R zależnego od długości przewodu:
\[P\,=\,\frac{U_0^2U_s^2P_s}{\left(RP_s+U_s^2\right)^2}\,=\,\frac{U_0^2U_s^2P_s}{\left(\frac{R_0}{l_0}lP_s+U_s^2\right)^2}\]Możemy uprościć powyższe równanie:
\[P\,=\,\frac{U_0^2U_s^2P_s}{\left(\frac{lR_0P_s+U_s^2l_0}{l_0}\right)^2}\]i wyrazić moc kuchenki jako funkcję długości przewodu. Ta funkcja jest dana wyrażeniem:
\[P\,=\,\frac{U_0^2U_s^2P_sl_0^2}{\left(U_s^2l_0+R_0P_s\bf{l}\right)^2}\]Jest to funkcja wymierna z kwadratowym wielomianem z mianowniku. Długość przewodu l jest widoczna w powyższym równaniu.
Znanymi wartościami są:
U0 = 230 V, Ps = 2 000 W, Us = 230 V, l0 = 60 m, R0 = 1,2 Ω
Możemy teraz sporządzić tabelę z długością przewodu od l = 0 do 2 000 m i mocą grzałki:
l [m] 0 400 800 1 200 1 600 2 000 P [W] 2 000 1 179 776 550 410 317 Odpowiedź
Napięcie chwilowe prądu płynącego przez grzałkę wynosi 220 V, a moc chwilowa 1830 W.