Cyklotron
Kod zadania: 1050
Ciężkie jądra wodoru, deuterony, przyspieszane są w akceleratorze kołowym, cyklotronie. Określ częstotliwość, jaką musi mieć źródło napięcia cyklotronu, jeżeli pole magnetyczne w akceleratorze wynosi 1,5 T, a masa deuteronu to 3,3·10-27 kg?
Jaki powinien być promień, po jakim poruszają się cząstki w cyklotronie, aby opuszczały go posiadając energię kinetyczną równą 16 MeV? Ile razy deuteron przebędzie odległość między duantami w cyklotronie, gdy różnica potencjałów między nimi będzie wynosiła 50 kV?
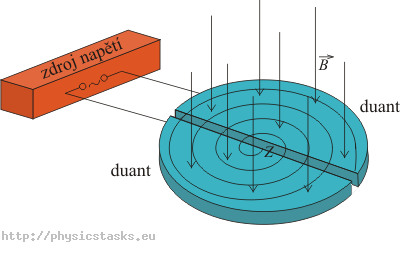
Opis działania cyklotronu (zasada)
Cyklotron to urządzenie, które przyspiesza naładowane cząstki, tzn. pozwala im uzyskać dużą energię kinetyczną. Wysoko energetyczne cząstki wykorzystywane są w badaniach jądrowych i medycynie w celu uzyskania radioaktywnych leków (kontrastu), mających służyć diagnostyce i terapii.
Cyklotron składa się z dwóch pół przewodów walcowych w kształcie litery D, otwartych na płaskiej stronie. Przewody te wykonane są z materiału nieferromagnetycznego (np. miedzianej płyty) i nazywane są duantami. Duanty znajdują się w jednorodnym polu magnetycznym o dużej wartości indukcji magnetycznej, prostopadłej do przewodu. Przewody podłączone są do źródła napięcia zmiennego. Naładowana cząstka przyspieszana jest przez pole elektryczne w przestrzeni między duantami do prędkości, z jaką wpada prostopadle do pola magnetycznego jednego z duantów.
Pole magnetyczne zakrzywia tor cząstki, tak więc poruszają się one po pół – okręgach. Gdy cząstka opuszcza duant, pole elektryczne między duantami zmienia swoją orientację, cząstka jest przyspieszana ponownie w kierunku drugiego duantu. Większa prędkość cząstki oznacza większy promień kołowej trajektorii. Proces ten jest powtarzany, tym samym tworzy trajektorie składającą się z pół – okręgów (patrz rysunek do zadania). Gdy promień toru cząstki zrówna się z promieniem cyklotronu, cząstki o wysokiej energii kinetycznej opuszczają urządzenie.
W cyklotronie wzrasta nie tylko prędkość cząstki, ale i długość jej trajektorii (promień pół-okręgu), tak że czas jednego okrążenia cyklotronu pozostaje stały (spójrz szczegółowe rozwiązanie zadania). Dzięki temu duanty można podłączyć do źródła pola elektrycznego o stałej częstotliwości. Zmiana częstotliwości pola elektrycznego w zależności od tego, jak cząstki są przyspieszane, nie jest tu konieczna.
Analiza
Deuteron, który „wyleciał” ze źródła umieszczonego w centrum cyklotronu, początkowo porusza się w kierunku ujemnie naładowanego duantu (deuteron jest cząstką o ładunku dodatnim). Cząstka zostaje przyspieszona. W przestrzeni między duantami nie „odczuwa” ona działania (wpływu) pola elektrycznego, gdyż ono tam nie występuje. Pole magnetyczne nie jest ekranowane przez duanty, także deuteron będzie poruszał się (w obszarze duantów) po torze kołowym, którego promień zależy od prędkości cząstki.
W czasie kiedy deuteron porusza się w kierunku ujemnie naładowanego duantu, napięcie między dwoma duantami zmieni swoją polaryzację. Cząstka będzie miała przed sobą znowu ujemnie naładowany duant, a wiec znowu jest przyspieszana. Proces ten trwa, deuteron krąży dzięki oscylacji napięcia między duantami, do momentu aż poruszając się „po spirali” osiągnie krawędź duantu i opuści cyklotron.
Aby deuteron był skutecznie przyspieszany, częstotliwość f, z jaką deuteron krąży w polu magnetycznym musi być równa częstotliwości źródła zasilania fz. Jeżeli częstotliwość generatora jest równa częstotliwości obiegu cząstek, to są one przyspieszane podczas przelotu między duantami. Aby energia poruszającego się po orbicie kołowej protonu wzrosła, częstotliwość fz (źródła) w przestrzeni między duantami musi być równa częstotliwości, z jaką cząstka orbituje w polu magnetycznym.
Jeżeli interesuje nas ile razy deuteron przebiegnie między duantami w akceleratorze, w celu uzyskania wymaganej (pożądanej) energii, należy pamiętać iż przy wyjściu cząstki z centrum cyklotronu jej energia kinetyczna jest na tyle mała, że można ją zaniedbać. Za każdym razem kiedy cząstka przyspiesza zyskuje ona energię proporcjonalną do napięcia między duantami.
Rozwiązanie a)
Deuterony o ładunku \(e\) wprowadzono w jednorodne pole magnetyczne o indukcji \(\vec{B}\) i prędkości \(\vec{v}\), która jest prostopadła do wektora indukcji \(\vec{B}\). Siła magnetyczna (siła Lorentza) \(\vec{F}_m\) działająca na cząstkę ma wartość
\[F_m=evB.\]W ruchu jednostajnym po okręgu występuje siła dośrodkowa, której wartość F wynosi:
\[F=ma=\frac{mv^2}{r}.\]Rolę siły dośrodkowej \(\vec{F}\) odgrywa w naszym przypadku siła magnetyczna \(\vec{F}_m\). Przyrównując ich wartości otrzymamy
\[evB=\frac{mv^2}{r}.\]Z powyższego równania otrzymamy promień okręgu, po którym poruszają się cząstki
\[r=\frac{mv}{eB}.\tag{1}\]Połowa okresu \(\frac{T}{2}\) (tj. czas jednego obiegu półokręgu) równa jest obwodowi półkola πr dzielonemu przez prędkość cząstkiv, tak więc
\[\frac{T}{2}=\frac{\pi r}{v}=\frac{\pi}{v}\frac{mv} {eB}=\frac{\pi m}{eB}.\]Okres obiegu T nie zależy tak od prędkości cząstek, jak i ich energii, tak więc czas jaki upłynął między dwoma przejściami między duantami podczas przyspieszania jest taki sam.
Dla częstotliwości f jest prawdą
\[f=\frac{1}{T}=\frac{eB}{2\pi m}.\]Aby cyklotron przyspieszał także protony, częstotliwość f, z jaką proton porusza się po okręgu w polu magnetycznym powinna być równa częstotliwości źródła napięcia fz
\[f_{z}=f=\frac{eB}{2\pi m}.\]Ładunek e jest zawsze stały. W przypadku nierelatywistycznym, takim jak nasz, stała jest także masa cząstki m. Źródło napięcia w jednej stałej częstotliwości fz. Cyklotron można dostroić przy użyciu zmiennego pola magnetycznego dopóki nie pojawi się wiązka przyspieszanych protonów.
Rozwiązanie b)
Zważywszy, że w chwili początkowej energia kinetyczna deuteronu była zaniedbywanie mała (prawie zero), energia kinetyczna jaką zyska cząstka o ładunku e przyspieszana napięciem U wynosi
\[E_k=eU.\]Deuteron, musi przejść n-krotnie między duantami, aby osiągnąć pożądaną energię Emax
\[E_\mathrm{max}=nE_k.\]Liczbę przejść deuteronu między duantami można wyrazić wtedy
\[n=\frac{E_\mathrm{max}}{E_k}=\frac{E_\mathrm{max}}{Ue}.\]Promień duantu R odpowiada promieniowi okręgu Rmax po jakim porusza się cząstka o maksymalnej energii. Promień cyklotronu wyraża relacja (1)
\[R_\mathrm{max}=\frac{mv}{eB}.\]Przy maksymalnej energii kinetycznej deuteronu, cząstki będą poruszać się z prędkością
\[E_\mathrm{max}=\frac{1}{2}mv^2\,\,\,\,\Rightarrow\,\,\,\, v=\sqrt{\frac{2E_\mathrm{max}}{m}}.\]Promień duantu Rmax będzie wtedy równy
\[R_\mathrm{max}=\frac{\sqrt{2mE_\mathrm{max}}}{eB}.\]Zapis i podstawienie danych liczbowych
\[e \,\dot{=}\, 1{,}6\cdot {10^{-19}}\,\mathrm{C}\] \[m \,\dot{=}\, 3{,}3 \cdot {10^{-27}}\,\mathrm{kg}\] \[B=1{,}5\,\mathrm{T}\] \[U = 50\,\mathrm{kV}\] \[E_\mathrm{max} = 16\,\mathrm{MeV}\,\dot{=}\,2{,}56\cdot {10^{-12}}\,\mathrm{J}\] \[f_{z} = \,?\] \[n=\,?\]
\[f_{z}=\frac{eB}{2\pi m}=\frac{1{,}6\cdot {10^{-19}}\cdot 1{,}5}{2\pi\cdot3{,}3 \cdot {10^{-27}}}\,\dot{=}\, 11 \cdot {10^{6}}\,\mathrm{s^{-1}}\] \[n=\frac{E_\mathrm{max}}{Ue}=\frac{2{,}56\cdot {10^{-12}}}{50\cdot {10^{3}}\cdot1{,}6\cdot {10^{-19}}}=320\] \[R=\frac{\sqrt{2E_\mathrm{max}m}}{eB}=\frac{\sqrt{2\cdot{ 2{,}56}\cdot {10^{-12}}\cdot 3{,}3 \cdot {10^{-27}}}}{1{,}6\cdot {10^{-19}}\cdot 1{,}5}\,\mathrm{m}\,\dot{=}\,0{,}54\,\mathrm{m}=54\,\mathrm{cm}\]Odpowiedź
Źródło pola elektrycznego ma częstotliwość w przybliżeniu równą 11·106 s-1. Deuteron, aby osiągnął określoną ilość energii będzie musiał przejść między duantami 320 razy. Promień cyklotronu równy jest promieniowi cząstki przyspieszonej do żądanej (maksymalnej) energii i wynosi 54 cm.



