Transformator - obwody prądu zmiennego
Kod zadania: 1004
Uzwojenie pierwotne transformatora ma 500 zwojów, a uzwojenie wtórne 10 zwojów.
a) Jaka będzie wartość napięcia wtórnego, jeśli napięcie pierwotne na transformatorze ma wartość 120 V ?
b) Jaki prąd popłynie w uzwojeniu pierwotnym i wtórnym, jeżeli do uzwojenia wtórnego podłączony jest rezystor o oporze 15 Ω?
Zapis danych
Z zadania wiemy:
Liczba zwojów w uzwojeniu pierwotnym: N1 = 500 Liczba zwojów w uzwojeniu wtórnym: N2 = 10 a) napięcie w uzwojeniu pierwotnym: U1 = 120 V b) opór podłączony do uzwojenia wtórnego: R = 15 Ω Chcemy znaleźć:
a) napięcie wtórne: U2 = ? (V) b) natężenie prądu w uzwojeniu pierwotnym: I1 = ? (A) natężenie prądu w uzwojeniu wtórnym: I2 = ? (A) Podpowiedź a)
W części a) mamy do czynienia z relacją napięcia na poszczególnych cewkach transformatora i liczbą zwojów.
Podpowiedź: Transformator, przekładnia transformatora
Napięcie prądu zmiennego możemy zmienić na inne, ale o takiej samej częstotliwości przy wykorzystaniu transformatora. Zasada działania transformatora oparta jest o zjawisko indukcji elektromagnetycznej. Na wspólnym zamkniętym rdzeniu nawinięte są dwie cewki. Uzwojenie pierwotne podłączone jest do napięcia sieciowego. Przepływający przez uzwojenie pierwotne prąd zmienny wywołuje powstanie zmiennego pola magnetycznego. To zmienne pole magnetyczne indukuje w uzwojeniu cewki wtórnej przepływ prądu elektrycznego. Ponieważ pole magnetyczne jest wspólne dla obu cewek, w każdym z uzwojeń, pierwotnym i wtórnym, mamy takie samo (stałe) napięcie Uz.
Napięcie na uzwojeniu pierwotnym: \(U_1=N_1 U_z\)
Napięcie na uzwojeniu wtórnym: \(U_2=N_2 U_z\)
gdzie N1 i N2oznaczają liczbę zwojów na uzwojeniu pierwotnym i wtórnym, odpowiednio.
Napięcie na jednym zwoju wynosi:
\[U_z=\frac{U_2}{N_2}=\frac{U_1}{N_1}.\]Dlatego możemy zapisać:
\[\frac{U_2}{U_1}=\frac{N_2}{N_1}=k,\]gdzie k nazywamy przekładnią transformatora.
Podpowiedź b)
Aby rozwiązać podpunkt b) skorzystamy z wyrażenia na moc prądu elektrycznego. W transformatorze idealnym moc na uzwojeniu pierwotnym równa jest mocy na uzwojeniu wtórnym. Korzystamy z prawa Ohma.
Analiza
Dla cewek transformatora, stosunek napięcia na obu cewkach jest stały i odpowiada stosunkowi liczby zwojów. Stosunek ten nazywamy przekładnią transformatora.
Jeżeli uzwojenie wtórne jest odłączone od zasilania, pomimo to transformuje się w nim napięcie proporcjonalne do przekładni transformatora. Napięcie wtórne wyraża stosunek liczby zwojów i napięcia na uzwojeniu pierwotnym.
W idealnym przypadku, moc odbierana na uzwojeniu wtórnym jest równa mocy na uzwojeniu pierwotnym. Moc uzwojenia wtórnego wyraża się poprzez napięcie wtórne cewki, którą oblicza się w sekcji a) i oporność, do której cewka jest podłączona. Ponieważ napięcie w obu obwodach jest znane, wyrazimy natężenie prądu pierwotnego. Prąd na uzwojeniu wtórnym otrzymamy z prawa Ohma.
a) Rozwiązanie
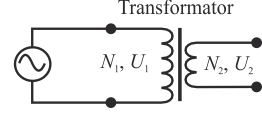
W rozwiązaniu zadania skorzystamy z tego, że stosunek napięcia wtórnego i pierwotnego jest stały i równy stosunkowi liczby zwojów w odpowiednich cewkach:
\[k=\frac{U_2}{U_1}=\frac{N_2}{N_1}\]Wyrazimy napięcie na uzwojeniu wtórnym:
\[U_2=\frac{N_2}{N_1}\,U_1\]
Po podstawieniu wartości liczbowych dostajemy:
\[U_2=\frac{10}{500}\cdot 120 \,\mathrm V=2{,}4 \,\mathrm V\]b) Rozwiązanie
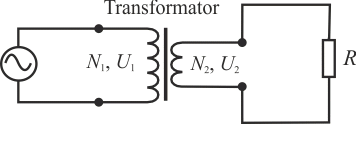
Natężenie prądu na uzwojeniu wtórnym uzyskamy z prawa Ohma. W obwodzie znajduje się opornik o znanym oporze, a napięcie wyznaczyliśmy w poprzednim podpunkcie:
\[I_2=\frac{U_2}{Z}\] \[I_2=\frac{U_2}{R}.\]Przy obliczeniu natężenia prądu w uzwojeniu pierwotnym zakładamy, że transformator jest idealny tzn. nie ma w nim żadnych strat. Dla obu cewek jest zatem prawdziwe:
\[P_1=P_2\]Dla mocy P1 mamy:
\[P_1=U_1\,I_1\]Moc P2 możemy wyrazić jako:
\[P_2=U_2 I_2=\frac{(U_2)^2}{R}\]Podstawiając do poprzedniego związku wyrażamy natężenie prądu na uzwojeniu pierwotnym:
\[U_1 I_1=\frac{(U_2)^2}{R}\] \[I_1=\frac{(U_2)^2}{U_1 R}.\]
Po podstawieniu wartości liczbowych otrzymamy:
Natężenie prądu pierwotnego:
\[I_1=\frac{(2{,}4)^2}{120 {\cdot} 15}\,\mathrm A=3{,}2 \,\mathrm mA\]Natężenie prądu wtórnego:
\[I_2=\frac{2{,}4}{15}\,\mathrm A=0{,}16\,\mathrm A\]Odpowiedź
W uzwojeniu wtórnym indukuje się prąd o napięciu 2,4 V.
Po podłączeniu do uzwojenia wtórnego opornika, natężenie prądu płynącego w uzwojeniu pierwotnym będzie wynosiło 3,2 mA, a we wtórnym 0,16 A.



