Obwody prądu zmiennego - długość rozładowania lampy jarzeniowej (neonowej)

Kod zadania: 1007

Do źródła zmiennego napięcia o efektywnej wartości 230 V i częstotliwości 50 Hz podłączono jarzeniówkę. Do obwodu z jarzeniówką podłączony jest opornik o oporze 150 kΩ. Napięcie zapłonu jarzeniówki z opornikiem ma wartość 116 V, napięcie gasnące (przy którym neonówka gaśnie) ma wartość 87 V. Określ czas, przez jaki jarzeniówka świeci w pierwszej połowie okresu.

Uwaga: lampa żarowa opisana w zadaniu jest prawdziwą jarzeniówką, którą można znaleźć np.: w przełącznikach (wyłącznikach) światła w korytarzach budynku.

Zapis danych

Z zadania znamy:

Napięcie źródła:	U = 230 V
Częstotliwość napięcia źródłowego:	f = 50 Hz
Opór rezystora:	R = 150 kΩ
Zapalne napięcie jarzeniówki z opornikiem:	U_Z = 116 V
Gasnące napięcie jarzeniówki z rezystorem:	U_ZH = 87 V

Chcemy znaleźć:

Czas, w którym jarzeniówka świeci:

Δt = ? (s)

Podpowiedź 1 - napięcie zapłonu
Jarzeniówka zacznie świecić, jeżeli napięcie osiągnie wartość zapłonu Uz = 116 V. Świeci w czasie, kiedy wartość napięcia jest wyższa niż Uz = 116 V. Gdy napięcie spadnie poniżej UzH = 87 V, lampa gaśnie.
Podpowiedź 2
Pomyśl, jaki prąd ma harmoniczne zmienne napięcie. Jak związane są napięcie skuteczne i maksymalna wartość napięcia?
Podpowiedź 3
Przebieg napięcia opisuje funkcja sinus:

\[u(t)=U_m \sin{(\omega t)}\]
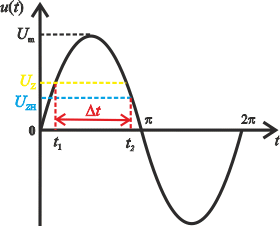
Analiza zadania
Jarzeniówka zaświeci, pod warunkiem, że napięcie osiągnie wartość napięcia zapłonu, a zgaśnie po osiągnięciu napięcia gaśnięcia. Naszym zadaniem jest znaleźć przedział czasowy, w którym napięcie osiągnie wartość napięcia zapalnego, a następnie napięcie gaśnięcia. W zadaniu wykorzystamy zależność napięcia od czasu (funkcja sinus).
Rozwiązanie

Czasowa zależność napięcia zmiennego jest opisana wzorem:

\[u(t)=U_m\, \sin{(\omega t)}.\]

Dla amplitudy napięcia U_m jest prawdziwe:

\[U_m=\sqrt{2}U,\] ,

gdzie U jest wartością napięcia efektywnego.

1) Napięcie zapłonu:

Szukamy czasu, dla którego napięcie chwilowe w obwodzie będzie równe napięciu zapłonu jarzeniówki, tj. rozwiązujemy równanie:
\[U_Z=U_m\, \sin{(\omega t_1)}.\] \[U_Z=\sqrt{2}U\sin{(\omega t_1)}.\]
Czas, w którym jarzeniówka się zapali:
\[\sin{(\omega t_1)}=\frac{U_Z}{\sqrt{2} U}\] \[\omega t_1=\mathrm{arcsin} (\frac{U_Z}{\sqrt{2} U})\] \[t_1=\frac{\mathrm{arcsin} (\frac{U_Z}{\sqrt{2} U})}{\omega}\]
Z wyrazu \(\mathrm{arcsin} (\frac{U_Z}{\sqrt{2} U})\) dostaniemy dwie wartości:

a) \(\mathrm{arcsin} (\frac{U_Z}{\sqrt{2} U})=\mathrm{arcsin} (\frac{116}{\sqrt{2}\cdot 230})=0{,}36\)

b) \(\mathrm{arcsin} (\frac{U_Z}{\sqrt{2} U})=\mathrm{arcsin} (\frac{116}{\sqrt{2}\cdot 230})=\pi - 0{,}36=2{,}78\)

Z tych dwóch wartości wybieramy tę mniejszą, w związku z tym a), ponieważ odpowiada ona wartości t₁ zaznaczonej na rysunku.

Podstawiamy wartości liczbowe do wyrażenia na czas, kiedy jarzeniówka się rozświetli:
\[t_{1}=\frac{\mathrm{arcsin} (\frac{U_Z}{\sqrt{2} U})}{\omega}=\frac{\mathrm{arcsin} (\frac{U_Z}{\sqrt{2} U})}{2 \pi f}=\frac{\mathrm{arcsin} (\frac{116}{\sqrt{2}\cdot 230})}{2\cdot \pi\cdot 50}\,\dot{=}\,1{,}16\,\mathrm ms\]

Uwaga: Jeśli nie otrzymałeś takiego samego wyniku, upewnij się czy kalkulator przełączony jest na radiany. Jeśli chcesz uzyskać wynik w stopniach trzeba podzielić przez 2π wynik wyrażony w radianach przemnożony przez 360°.

2) Napięcie gaśnięcia:

Szukamy czasu, w którym wartość chwilowego napięcia w obwodzie będzie równa napięciu gaśnięcia jarzeniówki, tj. rozwiązujemy równanie:
\[U_{ZH}= U_m \sin{(\omega t_2)}\] \[U_{ZH}=\sqrt{2} U \sin{( \omega t_2)}\]
Szukamy czasu, kiedy jarzeniówka zgaśnie:
\[\sin{(\omega t_2)}=\frac{U_{ZH}}{\sqrt{2} U}\] \[\omega t_2=\mathrm{arcsin} (\frac{U_{ZH}}{\sqrt{2} U})\] \[t_2=\frac{\mathrm{arcsin} (\frac{U_{ZH}}{\sqrt{2} U})}{\omega}\]
Z wyrazu \(\mathrm{arcsin} (\frac{U_{ZH}}{\sqrt{2} U})\) dostaniemy dwie wartości:

a) \(\mathrm{arcsin} (\frac{U_{ZH}}{\sqrt{2} U})=\mathrm{arcsin} (\frac{87}{\sqrt{2}\cdot 230})=0{,}27\)

b) \(\mathrm{arcsin} (\frac{U_{ZH}}{\sqrt{2} U})=\mathrm{arcsin} (\frac{87}{\sqrt{2}\cdot 230})=\pi - 0{,}27=2{,}87\)

Z tych wartości wybieramy tą większą, tu b), ponieważ odpowiada ona wartości t₂ zaznaczonej na rysunku.

Podstawiając do wyrażenia na czas wartości liczbowe, otrzymamy czas, kiedy jarzeniówka zgaśnie:
\[t_{2}=\frac{\mathrm{arcsin} (\frac{U_{ZH}}{\sqrt{2} U})}{\omega}=\frac{\mathrm{arcsin} (\frac{U_{ZH}}{\sqrt{2} U})}{2 \pi f}=\frac{\mathrm{arcsin} (\frac{87}{\sqrt{2}\cdot 230})}{2\cdot \pi\cdot 50}\,\dot{=}\,9{,}14\,\mathrm{ms}\]

Przedział czasowy, w którym jarzeniówka będzie świeciła, uzyskamy odejmując wartość czasu uzyskanego z wartości argumentu funkcji sinus dla chwilowego napięcia:
\[\Delta t=t_2 - t_1 = \left(9{,}14-1{,}16\right)\, \mathrm{ms} \,\dot{=}\,8\, \mathrm{ms}\]
Odpowiedź
Przedział, w którym jarzeniówka będzie świeciła w pierwszej połowie okresu napięcia zmiennego wynosi: \( \Delta t=8\,\mathrm{ms}. \)
Komentarz
Zadanie zostało rozwiązane tylko dla połowy okresu napięcia zmiennego. Podczas całego okresu jarzeniówka zabłyśnie dwa razy, dla prądu płynącego w obu kierunkach.