Przenoszenie przewodu w polu magnetycznym
Kod zadania: 1005
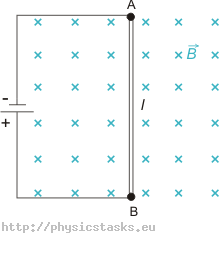
Przewód o długości 1m (odcinek AB na rysunku) i oporności 2 Ω umieszczono w polu magnetycznym o indukcji 0,1 T. Przewód podłączony jest do napięcia 1 V.
a) Określ natężenie prądu I płynącego przez przewód, jeśli:
- przewód jest w spoczynku,
- przewód porusza się z prędkością 4 m/s w prawą stronę,
- przewód porusza się z prędkością 4 m/s w lewo.
b) W którą stronę i jak szybko (z jaką prędkością) należy przenieść przewód aby nie popłynął przez niego żaden prąd? W jakim kierunku należy przesunąć przewód aby popłynął w nim taki prąd jak gdyby był w spoczynku?
Podpowiedź
Jaki warunek musi być spełniony, aby w obwodzie indukowała się siła elektromotoryczna (indukowało się napięcie)? Kiedy zostanie ona dodana do napięcia źródła, a kiedy odjęta?
Analiza a)
W pętli pokazanej na rysunku siła elektromotoryczna wywołana jest (indukuje się) zmianą strumienia magnetycznego przechodzącego przez powierzchnię pętli. Strumień magnetyczny jest tutaj rozumiany jako „liczba linii pola magnetycznego przechodząca przez obszar objęty przez przewód”. Istotna jest, nie liczba linii pola magnetycznego przechodzących przez obszar pętli, ale zmiana tej liczby. Natężenie i napięcie prądu indukowanego zależą od tempa zmian liczby linii pola magnetycznego. Dlatego w pierwszym przypadku (kiedy przewód jest w spoczynku) pole magnetyczne nie wpływa na przewód. Natężenie prądu obliczymy korzystając z prawa Ohma.
W drugim przypadku, przewód porusza się ze stałą prędkością, zwiększając tym samym zawartość (obszar) pętli, zwiększeniu ulega strumień magnetyczny. W obwodzie indukuje się prąd, który wytwarza wokół przewodu pole magnetyczne. Linie wtórnego pola magnetycznego mają taki kierunek, że przeciwdziałają zmianie strumienia magnetycznego (będą dążyć do zmniejszenia strumienia). Ich kierunek jest przeciwny do kierunku zewnętrznego pola magnetycznego, tak więc pole to skierowane jest „ do nas”. Przy wykorzystaniu zasady Ampere’a można określić kierunek prądu indukowanego. Kciuk wskazuje kierunek linii pola magnetycznego, a zakrzywione palce kierunek prądu w przewodniku (płynie w lewą stronę). Kierunek prądu indukowanego i prądu ze źródła napięcia jest taki sam, więc możemy je zsumować. Podobnie dla napięcia, gdzie napięcie jest sumą napięcia indukowanego (elektromotorycznej) i napięcia akumulatora.
W trzecim przypadku, przewód porusza się ze stałą prędkością w lewo, obszar pętli kurczy się, zmniejsza się liczba linii pola magnetycznego przechodzącego przez obszar pętli. W obwodzie indukuje się prąd. Wokół przewodnika pojawia się pole magnetyczne. Linie indukowanego pola magnetycznego będą miały taki kierunek, że przeciwdziałają zmianie strumienia magnetycznego (chcą go zwiększyć). Zgodnie z regułą Ampere’a prąd indukowany płynie tym razem w prawo. Kierunek prądu indukowanego i prądu z akumulatora są przeciwne, więc zostaną odjęte. Podobnie dla napięcia, gdzie napięcie wypadkowe jest różnicą napięcia pochodzącego od źródła napięcia i napięcia indukowanego.
Rozwiązanie a)
W pierwszym przypadku nie jest indukowana żadna siła elektromotoryczna (napięcie), natężenie prądu obliczymy wprost z prawa Ohma
\[U=R I \,\,\,\Rightarrow\,\,\,I_\mathrm{klid}=\frac{U}{R}\]W drugim przypadku natężenie prądu obliczymy także z prawa Ohma, gdzie U jest napięciem źródła, a Ui napięciem indukowanym.
\[I_\mathrm{vpravo}=\frac{U+U_i}{R}\]Wielkość indukowanej siły elektromotorycznej równa jest zmianie strumienia magnetycznego przecinającego pętlę z prądem
\[U_i=\frac{\Delta \Phi}{\Delta t}\]Dla strumienia magnetycznego mamy
\[\Phi =B S cos \alpha,\]gdzie α jest kątem między liniami pola magnetycznego a normalną (prostopadłą) do powierzchni pętli, w naszym przypadku α = 0° i cos α = 1. Obszar pętli S zastąpimy
\[S = l v t\]Dla napięcia indukowanego otrzymamy
\[U_i = \frac{\Delta (Blvt)}{\Delta t}\] \[U_i = \frac{Blv\Delta t}{\Delta t}=Blv\]Podstawiając do wzoru na natężenie prądu otrzymamy
\[I_\mathrm{vpravo}=\frac{U+Blv}{R}\]W trzecim przypadku natężenie prądu jest również obliczane z prawa Ohma, przy czym od napięcia źródła odejmujemy napięcie indukowane w przewodzie
\[I_\mathrm{vlevo}=\frac{U-U_i}{R}\]Wartość indukowanego napięcia zależy od szybkości zmian strumienia magnetycznego. Przewód w obu sytuacjach, przenoszony jest z tą samą prędkością, więc wartość napięcia indukowanego w obu przypadkach jest taka sama.
\[I_\mathrm{vlevo}=\frac{U-Blv}{R}\]Zapis i podstawienie danych liczbowych a)
\[l = 1\,\mathrm{m}\] \[R=2\,\mathrm{\Omega}\] \[B=0{,}1\,\mathrm{T}\] \[U=1\,\mathrm{V}\] \[I_{\mathrm{klid}}=\,? \] \[I_{\mathrm{vpravo}}=\,? \] \[I_{\mathrm{vlevo}}=\,? \]
\[I_{\mathrm{klid}}=\frac{U}{R}=\frac{1}{2}\,\mathrm{A}=0{,}5\,\mathrm{A}\] \[I_{\mathrm{vpravo}}=\frac{U+U_i}{R}=\frac{U+Blv}{R}=\frac{1+0{,}1\cdot{1}\cdot{4}}{2}\,\mathrm{A}=0{,}7\,\mathrm{A}\] \[I_{\mathrm{vlevo}}=\frac{U-U_i}{R}=\frac{U-Blv}{R}=\frac{1-0{,}1\cdot{1}\cdot{4}}{2}\,\mathrm{A}=0{,}3\,\mathrm{A}\]Odpowiedź a)
Jeśli przewód jest w spoczynku przepływa przez niego prąd o natężeniu 0,5 A. Jeśli przewód porusza się ze stała prędkością 4 m/s w prawą stronę, przez przewód płynie prąd o natężeniu 0,7 A, Jeśli przewód porusza się z prędkością j.w. tym razem w lewo, to popłynie przez niego prąd o natężeniu 0,3 A. .
Analiza b)
Aby przez przewód nie przepłynął żaden prąd, musi indukować się w nim napięcie równe co do wartości napięciu pochodzącemu ze źródła.
Aby przez przewód popłynął stały prąd, tak jakgdyby przewód był w spoczynku, nie należy zmienić strumienia pola magnetycznego, „liczby linii pola przechodzącego przez powierzchnię pętli utworzonej z przewodnika”. Przewód można poruszać tylko w kierunku linii indukcji.
Rozwiązanie b)
Z prawa Ohma obliczymy natężenie prądu.
\[I=\frac{U\pm U_i}{R}\]Aby przez przewód nie popłynął prąd, napięcie jakie indukuje się w obwodzie musi być równe napięciu źródła prądu
\[U=U_i\]Napięcie indukowane otrzymane w poprzedniej części zadania wynosiło
\[U=U_i=Bvl\]Wyznaczając nieznaną prędkość v dostajemy
\[v=\frac {U}{Bl}\]Kierunek ruchu pętli określa rozwiązanie a), gdzie przesunięcie przewodu w lewą stronę powodowało zmniejszenie się strumienia magnetycznego, dochodząc do zera. W naszym przypadku przewód zostanie przesunięty w lewo z prędkością v.
Jeśli prędkość z jaką porusza się przewód w lewą stronę byłaby większa, wówczas wartość indukowanego napięcia przewyższałaby napięcie otrzymywane ze źródła i prąd całkowity będzie ujemny (popłynie w przeciwnym kierunku).
Zapis i podstawienie danych liczbowych b)
\[l = 1\,\mathrm{m}\] \[R=2\,\mathrm{\Omega}\] \[B=0{,}1\,\mathrm{T}\] \[U=1\,\mathrm{V}\] \[I=0 \,\mathrm{A}\] \[v=\,? \]
\[v=\frac{U}{Bl}=\frac{1}{0{,}1\cdot {1}}\,\mathrm{m\,s}^{-1}=10\,\mathrm{m\,s}^{-1}\ \]Odpowiedź b)
Aby przez przewód nie przepłynął prąd powinien poruszać się on z prędkością 10 m/s w lewo.
Aby przez przewód popłynął prąd, jak w spoczynku, musi się poruszać w kierunku linii pola indukowanego.



