Elektrony przyspieszone w akceleratorze
Kod zadania: 1043
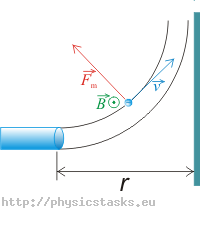
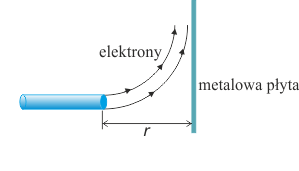
Elektrony o energii kinetycznej Ek opuszczają akcelerator. W odległości r od miejsca opuszczenia akceleratora znajduje się metalowa płyta ustawiona prostopadle do wiązki elektronów (patrz rysunek). Wykaż, że wiązka nie uderzy w metalową płytę, jeśli zostanie odchylona polem magnetycznym \(\vec{B}\) o indukcji
\[B=\sqrt{\frac{2mE_k}{e^{2}r^{2}}},\]gdzie m i e to odpowiednio masa i ładunek elektronu. Jaki musi być zwrot wektora indukcji pola magnetycznego?
Określ wartość indukcji, jeśli elektrony mają energię 5 keV, a odległość od wylotu akceleratora do płytki wynosi 5 mm.
Podpowiedź
Elektron w polu magnetycznym może odchylić siła Lorentza, działająca prostopadle do kierunku ruchu.
Analiza
Gdyby nie było pola magnetycznego, elektrony po opuszczeniu akceleratora poruszałyby się ruchem jednostajnym po linii prostej i uderzyły w płytkę. Jeśli chcemy im tego zabronić, musimy zmienić kierunek ich ruchu.
Tor elektronu zakrzywimy wprowadzając pole magnetyczne. Gdy naładowana cząstka (wiązka cząstek) porusza się w polu magnetycznym, działa na nią siła Lorentza. Jeśli zadziała jako siła dośrodkowa, zakrzywi tor cząstek. Cząstki poruszać się będą po torze, który jest fragmentem okręgu.
Wartość indukcji określimy z porównania siły Lorentza i siły dośrodkowej.
Przy określaniu kierunku wektora indukcji magnetycznej skorzystamy z faktu, że siła Lorentza jest maksymalna, gdy wektory prędkości i indukcji są do siebie prostopadłe. Siła Lorentza działa prostopadle do płaszczyzny obu wymienionych wektorów. W naszym przypadku wektor indukcji powinien więc być prostopadły do płaszczyzny rysunku. Trzeba jeszcze określić (przy pomocy reguły Fleminga lub śruby prawoskrętnej), czy zwrot będzie przed, czy za płaszczyznę rysunku.
Rozwiązanie
Zauważmy, że w polu magnetycznym o indukcji \(\vec{B}\) porusza się cząstka o ładunku e i szybkości v. Wygodnie będzie przyjąć, żeby wektor indukcji magnetycznej był prostopadły do wektora prędkości, gdyż wówczas na cząstkę działa siła maksymalna \(\vec{F}_m\), a jej wartość
\[F_m = evB.\]Siła Lorentza \(\vec{F}_m\) działa prostopadle do kierunku ruchu, jest więc siłą dośrodkową. Wiązka cząstek będzie się poruszać po okręgu. Na siłę dośrodkową podstawimy
\[F_d=m\frac{v^2}{r}.\]Oba wzory porównujemy
\[F_m=F_d,\] \[evB=\frac{mv^2}{r}\]i obliczamy wartość indukcji B
\[B=\frac{mv}{re}.\]Ponieważ nie znamy prędkości elektronu v, wyznaczymy ją na podstawie energii kinetycznej Ek
\[E_k=\frac{1}{2}mv^2\hspace{27px}\Rightarrow\hspace{27px}\ v=\sqrt{\frac{2E_k}{m}}.\]Podstawiamy do wzoru na wartość indukcji magnetycznej B
\[B=\frac{m}{re}\sqrt{\frac{2E_k}{m}}.\]Po uproszczeniu otrzymujemy wyrażenie zgodne z treścią zadania
\[B=\sqrt{\frac{2mE_k}{r^2e^2}}.\]Określenie zwrotu wektora indukcji magnetycznej B
Zwrot wektora indukcji magnetycznej możemy określić przy pomocy:
1) reguły Fleminga lewej dłoni
Przyłóżmy do przewodnika lewą dłoń tak, aby wyprostowane palce wskazywały kierunek prądu, a linie pola magnetycznego (a więc i wektor \(\vec{B}\)) wchodziły w dłoń; wówczas odchylony kciuk wskaże zwrot wektora siły\(\vec{F}_m\), działającej na przewodnik
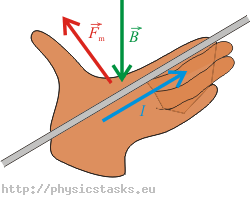
Kierunek prądu w przewodniku to kierunek ruchu naładowanych dodatnio cząstek. W naszym przypadku mamy wiązkę elektronów, a więc cząstek o ładunku ujemnym. Będziemy więc palce lewej dłoni kierować w stronę przeciwną do kierunku ruchu elektronów. Na rysunku elektrony odchylane są do góry, taki więc zwrot musi mieć i siła Lorentza. Wektor indukcji magnetycznej będzie więc mieć zwrot przed płaszczyznę rysunku (do nas).
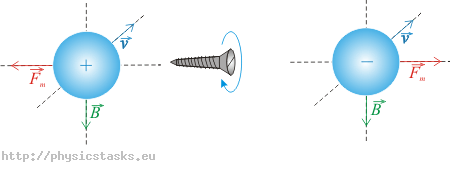
2) Reguła śruby prawoskrętnej
Obracamy śrubę prawoskrętną od kierunku wektora prędkości \(\vec{v}\) do kierunku wektora indukcji magnetycznej \(\vec{B}\) (obracamy zawsze o kąt mniejszy niż \(\pi\)); zwrot ruchu śruby jest zgodny ze zwrotem działającej siły \(\vec{F}_m\). Przy ładunku ujemnym, zwrot siły \(\vec{F}_m\) jest przeciwny.
Korzystając z tej reguły, otrzymujemy zwrot indukcji magnetycznej \(\vec{B}\) jak wyżej.
Zapis danych i obliczenia
\(E_k=5\,\mathrm{keV}\) - elektron przyspieszany napięciem 5000V
\[E_k=8\cdot {10^{-16}}\,\mathrm{J}\] \[r=5\,\mathrm{mm}=5 \cdot{ 10^{-3}}\,\mathrm{m}\]Do otrzymanego wyrażenia podstawiać będziemy energię w dżulach:
Z tablic:
\[m_e=9{,}1 \cdot {10^{-31}}\,\mathrm{kg}\] \[e=1{,}6\cdot {10^{-19}}\,\mathrm{C}\]
\[B=\sqrt{\frac{2mE_k}{e^{2}r^{2}}}=\sqrt{\frac{2\cdot {9{,}1}\cdot {10^{-31}}\cdot8\cdot{ 10^{-16}}}{\left(1{,}6\cdot {10^{-19}}\right)^{2}\left(5 \cdot {10^{-3}}\right)^{2}}}\,\,\,\mathrm{T}\,\dot{=}\,0{,}048\,\mathrm{T}\] \[B\,\dot{=}\,48\,\mathrm{mT}\]Odpowiedź
Pokazaliśmy, że możemy zabronić wiązce elektronów dotrzeć do płytki, jeżeli odchylimy go polem magnetycznym o wartości
\[B=\sqrt{\frac{2mE_k}{e^{2}r^{2}}}.\]Dla podanych wartości liczbowych indukcja pola wynosi
\[B\,\dot{=}\,48\,\mathrm{mT}.\]Zwrot wektora indukcji magnetycznej - przed płaszczyznę rysunku (do nas).
Komentarz
Oczywiście w celu odchylenia wiązki elektronów dopuszczalny jest dowolny zwrot wektora indukcji prostopadle do kierunku ruchu elektronów.
W zadaniu przyjęto zgodnie z rysunkiem odchylenie w górę i stąd zwrot przed płaszczyznę rysunku. W rzeczywistości również zwrot za płaszczyznę zapewnia oczywiście podobny efekt z odchyleniem elektronów w dół.