Young’s Experiment including Impact of Diffraction

Task number: 1698

Determine the behaviour of intensity of light on the screen during the Young's interference experiment. The distance between two slits is \(b\). The width of the slits is \(d\). The distance between the slits and the screen is \(l\)

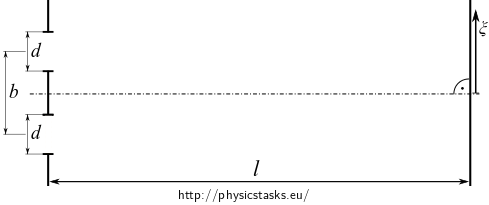
The width of the slits is negligible; therefore it is necessary to consider the bending phenomenon.
Assume that the time dependence of the electric field intensity at the plane of the slits is given described as \(\mathcal{E}_0 e^{i\omega t}.\)
Consider so called Fraunhofer diffraction, i.e. \(L \gg b\).

The electric field intensity at a given point can be determined by integration of contributions of the sources over the cross-section of the slits.

Links to related tasks
Before solving this task, we recommend to study the task Ohyb na štěrbině, which is a simpler variant of this task.

Young's interference experiment without diffraction can be found in the task Young’s Interference Experiment.

This task can also be solved without integrating a superposition of waves from two separate slits; see Ohyb na dvojité štěrbině alternativně. This approach, however, takes the results from the task Ohyb na štěrbině.
Theory
Both slots with non-negligible width can be modelled as continuous belts of line sources of cylindrical waves.

The belts of line sources are represented by line segments of yellow perpendicular projections.

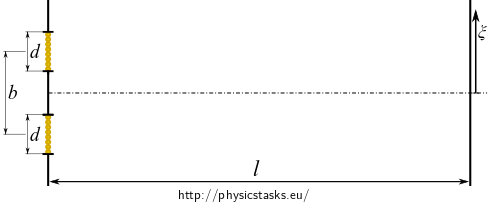
The electric field intensity of a cylindrical wave can be described by a function
\[ E(\rho) = \frac{\mathcal{E}_0}{\sqrt{\rho}}e^{i(\omega t - k\rho)}. \]
Different cylindrical waves with different coordinate \(\rho\) coming from different slits superpose at a certain point of the screen. The resulting electric field intensity can be found by the integration of line sources over the cross-section of the slits.

If the screen is sufficiently far from the slits, the cylindrical wave fronts can be considered nearly planar and we can use the relationship that applies for a plane wave
\[ I = \frac{1}{2z_0} EE^\star, \]
where \(z_0 = \sqrt{\frac{\mu_0}{\varepsilon_0}}\) is a constant and represents the characteristic impedance of vacuum.
Integral needed for calculation
To solve this task it is useful to know the integral of an exponential function with a multiplicative constant in the argument
\[ \int e^{\varphi x}\,\mathrm{d}x = \frac{e^{\varphi x}}{\varphi} + C. \]
Hint 1 – superposition of electric intensity
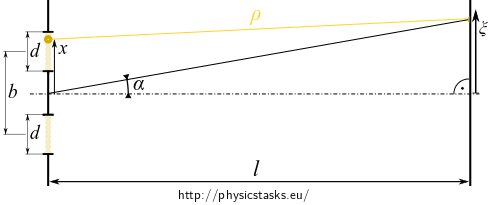
Write a mathematic representation of a cylindrical wave of a linear source with the coordinate \(x\).

Find the coordinate \(\rho\) using the distance \(l\), coordinate \(x\) of the imaginary line source and the coordinate \(\xi\) of a point on the screen. Adjust the relation considering that \(x \lt d\ll l\).

The resulting electric intensity is the sum of the partial contributions from all linear sources of the slit. The sources cover the slit continuously, assemble therefore the appropriate integral.
Solution of Hint 1 – superposition of electric intensity
The electric intensity at the point with the coordinate \(\xi\) of the screen corresponding to an elementary line source with coordinate \(x\) is
\[ \mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{\rho}} e^{i(\omega t - k\rho)} \mathrm{d}x, \tag{1}\]
where \(\rho\) is the distance between the stripe on the screen and the linear source and can be expressed by \(l,\xi, x\) as
\[ \rho = \sqrt{l^2 + (\xi-x)^2}. \tag{2}\]
Now we need two approximations:
1. We neglect the change of the loss of amplitude within the screen.
  
  In the relationship (1) the amplitude of electric intensity decreases as \(\sqrt\rho\). If the screen is sufficiently far, the differences in \(\rho\) and therefore the differences in global amplitude are therefore negligible the and variable expression \(\frac{1}{\sqrt\rho}\) can be approximated by a constant \(\frac{1}{\sqrt{l}}\). This leads to a more simple integral.
2. We adjust the relation for \(\rho\) taking into account that \(|x| \lt d \ll l\).
  
  We adjust the equation for \(\rho\)
  \[ \rho = \sqrt{l^2 + (\xi-x)^2} = \sqrt{l^2 + \xi^2 - 2\xi x + x^2} = \] \[ = \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{grey}{\frac{x^2}{l^2 + \xi^2}}}= \]
  The grey component can be left out: for large l it is negligible. Instead we add a negligibly small component (blue) to complete a square.
  \[ = \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{blue}{\frac{\xi^2 x^2}{\left(l^2 + \xi^2\right)^2}}}= \] \[ = \sqrt{l^2 + \xi^2}\bigg(1-\frac{\xi x}{l^2 + \xi^2} \bigg)= \] \[ = \sqrt{l^2 + \xi^2}-x\overbrace{\frac{\xi}{\sqrt{l^2 + \xi^2}}}^{\sin \alpha} =\sqrt{l^2 + \xi^2} - x\sin \alpha. \]
Previous approximations give us the following form of electric field intensity
\[ \mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{l}} e^{i(\omega t - k\rho)}\mathrm{d}x, \qquad \mathrm{where\,} \rho = \sqrt{l^2 + \xi^2} - x\sin \alpha. \]
The overall electric intensity at the point with coordinate \(\xi\) of the screen is the sum of the contributions of all line sources. Therefore
\[ E(\xi) = \int\limits_{\mathrm{1.\,štěr.}}\! \mathrm{d}E_x(\xi) + \int\limits_{\mathrm{2.\,štěr.}}\! \mathrm{d}E_x(\xi)= \] \[ =\int\limits_{\frac{b}{2}-\frac{d}{2}}^{\frac{b}{2}+\frac{d}{2}} \!\frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x + \int\limits_{-\frac{b}{2}-\frac{d}{2}}^{-\frac{b}{2}+\frac{d}{2}} \!\frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x. \]
Hint 2 – calculation of the integral
Determine both integrals that describe the behaviour of \(E(\xi)\)
\[ \underbrace{ \int\limits_{\frac{b}{2}-\frac{d}{2}}^{\frac{b}{2}+\frac{d}{2}} \!\frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x }_{\mathrm{denote\,}\iota_1} + \underbrace{ \int\limits_{-\frac{b}{2}-\frac{d}{2}}^{-\frac{b}{2}+\frac{d}{2}} \!\frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x. }_{\mathrm{denote\,}\iota_2} \]
Both integrals have the same integrand, differing only in the sign of the limits of the integral. Calculate the integrals \(\iota_1,\iota_2\) and then add up the results.

The exponential function can be written as a product of exponential functions; factor out the components that do not depend on the integration variable \(x\). The integral then can be easily integrated, i.e. \(\int e^{\varphi x}\,\mathrm{d}x = \frac{e^{\varphi x}}{\varphi}+C\). Substitute the limits and adjust the result.

Find the complex conjugate \(E^\star(\xi)\) of the resulting function \(E(\xi)\).
Solution of Hint 2 – calculation of the integral
We calculate both integrals \(\iota_1, \iota_2\) simultaneously
\[ \iota_{1{,}2} = \int\limits_{\pm\frac{b}{2}-\frac{d}{2}}^{\pm\frac{b}{2}+\frac{d}{2}} \! \frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x = \] \[ = \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \int\limits_{\pm\frac{b}{2}-\frac{d}{2}}^{\pm\frac{b}{2}+\frac{d}{2}} \! e^{ikx\sin \alpha}\,\mathrm{d}x = \]
We factor the constant out of the integral. Now we find the primitive function.
\[ = \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left[ \frac{e^{ikx\sin \alpha}}{ik\sin\alpha} \right]_{\pm\frac{b}{2}-\frac{d}{2}}^{\pm\frac{b}{2}+\frac{d}{2}} = \] \[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{\pm ik\frac{b}{2}\sin \alpha}e^{ik\frac{d}{2}\sin \alpha} - e^{\pm ik\frac{b}{2}\sin \alpha}e^{-ik\frac{d}{2}\sin \alpha} \right)= \]
In the previous step we substituted the limits. Now we factor the common exponential function out.
\[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{ik\frac{d}{2}\sin \alpha} - e^{-ik\frac{d}{2}\sin \alpha} \right) e^{\pm ik\frac{b}{2}\sin \alpha} = \] \[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{i\psi} - e^{-i\psi} \right) e^{\pm i\phi}, \]
where we denoted \(\psi = k\frac{d}{2}\sin \alpha\) and \(\phi=k\frac{b}{2}\sin \alpha\).

The behaviour of electric intensity is the sum of integrals \( \iota_1, \iota_2\), tj.
\[ E(\xi) = \iota_1 + \iota_2 = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{i\psi} - e^{-i\psi} \right) \left(e^{i\phi} + e^{-i\phi}\right). \]

Independently we adjust both parentheses with complex exponential functions. We represent them with sine and cosine functions (\(e^{i\varphi} = \cos \varphi + i \sin \varphi\)).
\[ \small e^{i\psi} - e^{-i\psi} = \cos \psi + i\sin \psi - \cos( -\psi) - i\sin (-\psi) = 2i\sin\psi, \] \[ \small e^{i\phi} + e^{-i\phi} = \cos \phi + i\sin \phi + \cos( -\phi) + i\sin (-\phi) = 2\cos\phi. \]

So we have
\[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} 2i\sin\psi \, 2\cos\phi = \] \[ = \frac{2 E_0 d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin \psi}{\psi} \cos \phi. \]
where we substituted for \(\sin\alpha\) from the relation \(\psi = k\frac{d}{2}\sin \alpha\)

We write a complex conjugate of the determined electric intensity
\[ E(\xi) = \frac{2 E_0 d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin \psi}{\psi} \cos \phi, \tag{3}\] \[ E^\star(\xi)= \frac{2 E_0 d}{\sqrt{l}} e^{-i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin \psi}{\psi} \cos \phi. \tag{4}\]
Hint 3 – behaviour of light intensity on the screen
At large distances from the slits, the parts of the cylindrical waves can be considered planar and thus the intensity of light can be calculated using the relationship
\[ I = \frac{1}{2z_0} EE^\star. \]
• Solutions of Hint 3 – behaviour of light intensity on the screen
We obtain the behaviour of light intensity by substituting (3) and (4) in the relation for intensity
\[ I = \frac{1}{2z_0} EE^\star= \overbrace{\frac{2E_0^2 d^2}{z_0l}}^{\mathrm{denoted\,}I_0} \underbrace{e^{i(\cdots)}e^{-i(\cdots)}}_{1} \frac{\sin^2 \psi}{\psi^2}\cos^2 \phi. \]
The intensity is thus described as follows:
\[ \begin{array}{cl} I = I_0 \color{green}{\frac{\sin^2 \psi}{\psi^2}}\color{blue}{\cos^2 \phi}, \qquad \mathrm{where}\quad & \psi = k\frac{d}{2}\sin \alpha, \\ & \phi = k\frac{b}{2}\sin \alpha. \end{array} \]
We can see that the behaviour is the product of diffraction functions:
- \(\color{green}{\frac{\sin^2 \psi}{\psi^2}}\), which we have calculated in the task Diffraction on One Slit,
- \(\color{blue}{\cos^2 \phi}\), which we have calculated in the task Double-Slit Interference Experiment.
In the following picture there is the behaviour of light intensity given by the product of the two diffraction functions.
OVERALL SOLUTION
The electric intensity at the point with the coordinate \(\xi\) of the screen corresponding to an elementary line source with coordinate \(x\) is
\[ \mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{\rho}} e^{i(\omega t - k\rho)} \mathrm{d}x, \]
where \(\rho\) is the distance between the stripe on the screen and the linear source and can be expressed by \(l,\xi, x\) as
\[ \rho = \sqrt{l^2 + (\xi-x)^2}. \]
Now we need two approximations:
1. We neglect the change in the loss of amplitude within the screen.
  
  In the relationship (1) the amplitude of electric intensity decreases as \(\sqrt\rho\). If the screen is sufficiently far, the differences in \(\rho\) and therefore the differences in global amplitude are therefore negligible the and variable expression \(\frac{1}{\sqrt\rho}\) can be approximated by a constant \(\frac{1}{\sqrt{l}}\). This leads to a more simple integral.
2. We adjust the equation for \(\rho\) taking into account that \(|x| \lt d \ll l\).
  
  We adjust the equation for \(\rho\)
  \[ \rho = \sqrt{l^2 + (\xi-x)^2} = \sqrt{l^2 + \xi^2 - 2\xi x + x^2} = \] \[ = \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{grey}{\frac{x^2}{l^2 + \xi^2}}}= \]
  The grey component can be left out: for large l it is negligible. Instead we add a negligibly small component (blue) to complete a square.
  \[ = \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{blue}{\frac{\xi^2 x^2}{\left(l^2 + \xi^2\right)^2}}}= \] \[ = \sqrt{l^2 + \xi^2}\bigg(1-\frac{\xi x}{l^2 + \xi^2} \bigg)= \] \[ = \sqrt{l^2 + \xi^2}-x\overbrace{\frac{\xi}{\sqrt{l^2 + \xi^2}}}^{\sin \alpha} =\sqrt{l^2 + \xi^2} - x\sin \alpha. \]
The previous approximations give us the following form of electric field intensity
\[ \mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{l}} e^{i(\omega t - k\rho)}\mathrm{d}x, \qquad \mathrm{kde\,} \rho = \sqrt{l^2 + \xi^2} - x\sin \alpha. \]
The overall electric intensity at the coordinate \(\xi\) on the screen is the sum of the contributions of all line sources. Therefore
\[ E(\xi) = \int\limits_{\mathrm{1.\,štěr.}}\! \mathrm{d}E_x(\xi) + \int\limits_{\mathrm{2.\,štěr.}}\! \mathrm{d}E_x(\xi)= \] \[ \underbrace{ \int\limits_{\frac{b}{2}-\frac{d}{2}}^{\frac{b}{2}+\frac{d}{2}} \!\frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x }_{\mathrm{denoted\,}\iota_1} + \underbrace{ \int\limits_{-\frac{b}{2}-\frac{d}{2}}^{-\frac{b}{2}+\frac{d}{2}} \!\frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x }_{\mathrm{denoted\,}\iota_2}. \]
We calculate both integrals \(\iota_1, \iota_2\) simultaneously
\[ \iota_{1{,}2} = \int\limits_{\pm\frac{b}{2}-\frac{d}{2}}^{\pm\frac{b}{2}+\frac{d}{2}} \! \frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x = \] \[ = \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \int\limits_{\pm\frac{b}{2}-\frac{d}{2}}^{\pm\frac{b}{2}+\frac{d}{2}} \! e^{ikx\sin \alpha}\,\mathrm{d}x = \]
We factor the constant out of the integral. Now we find the primitive function.
\[ = \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left[ \frac{e^{ikx\sin \alpha}}{ik\sin\alpha} \right]_{\pm\frac{b}{2}-\frac{d}{2}}^{\pm\frac{b}{2}+\frac{d}{2}} = \] \[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{\pm ik\frac{b}{2}\sin \alpha}e^{ik\frac{d}{2}\sin \alpha} - e^{\pm ik\frac{b}{2}\sin \alpha}e^{-ik\frac{d}{2}\sin \alpha} \right)= \]
In the previous step we substituted limits. Now we factor the common exponential function out.
\[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{ik\frac{d}{2}\sin \alpha} - e^{-ik\frac{d}{2}\sin \alpha} \right) e^{\pm ik\frac{b}{2}\sin \alpha} = \] \[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{i\psi} - e^{-i\psi} \right) e^{\pm i\phi}, \]
where we denoted \(\psi = k\frac{d}{2}\sin \alpha\) and \(\phi=k\frac{b}{2}\sin \alpha\).

The behaviour of electric intensity is the sum of integrals \( \iota_1, \iota_2\), i.e.
\[ E(\xi) = \iota_1 + \iota_2 = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{i\psi} - e^{-i\psi} \right) \left(e^{i\phi} + e^{-i\phi}\right). \]

Independently we adjust both parentheses with complex exponential functions. We represent them with sine and cosine functions (\(e^{i\varphi} = \cos \varphi + i \sin \varphi\)).
\[ \small e^{i\psi} - e^{-i\psi} = \cos \psi + i\sin \psi - \cos( -\psi) - i\sin (-\psi) = 2i\sin\psi, \] \[ \small e^{i\phi} + e^{-i\phi} = \cos \phi + i\sin \phi + \cos( -\phi) + i\sin (-\phi) = 2\cos\phi. \]

So we have
\[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} 2i\sin\psi \, 2\cos\phi = \] \[ = \frac{2 E_0 d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin \psi}{\psi} \cos \phi, \]
where we substituted from the relation \(\psi = k\frac{d}{2}\sin \alpha\) for \(\sin\alpha\)

We write a complex conjugate of the determined electric intensity
\[ E(\xi) = \frac{2 E_0 d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin \psi}{\psi} \cos \phi, \] \[ E^\star(\xi)= \frac{2 E_0 d}{\sqrt{l}} e^{-i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin \psi}{\psi} \cos \phi. \]
We obtain the behaviour of light intensity by substituting(3) and (4) in the relation for intensity
\[ I = \frac{1}{2z_0} EE^\star= \overbrace{\frac{2E_0^2 d^2}{z_0l}}^{\mathrm{ozn.\,}I_0} \underbrace{e^{i(\cdots)}e^{-i(\cdots)}}_{1} \frac{\sin^2 \psi}{\psi^2}\cos^2 \phi. \]
The intensity is thus described as follows
\[ \begin{array}{cl} I = I_0 \color{green}{\frac{\sin^2 \psi}{\psi^2}}\color{blue}{\cos^2 \phi}, \qquad \mathrm{kde}\quad & \psi = k\frac{d}{2}\sin \alpha, \\ & \phi = k\frac{b}{2}\sin \alpha. \end{array} \]
We can see that the behaviour is the product of diffraction functions:
- \(\color{green}{\frac{\sin^2 \psi}{\psi^2}}\), 2 which we have calculated in the task Diffraction on One Slit ,
- \(\color{blue}{\cos^2 \phi}\), which we have calculated in the task Double-Slit Interference Experiment.
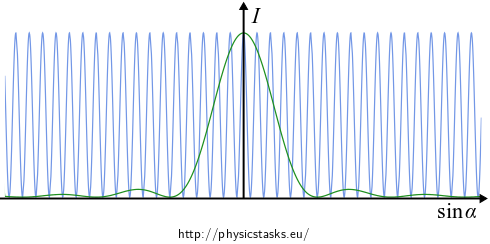
In the following picture there is the behaviour of light intensity given by the product of the two diffraction functions.
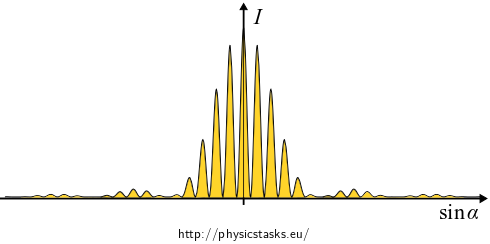
Answer
The behaviour of light intensity on the screen is described by the following function:
\[ \begin{array}{cl} I = I_0 \frac{\sin^2 \psi}{\psi^2}\cos^2 \phi, \qquad \mathrm{where}\quad & \psi = k\frac{d}{2}\sin \alpha, \\ & \phi = k\frac{b}{2}\sin \alpha, \\ & I_0 = \frac{2E_0^2 d^2}{z_0l}. \end{array} \]
Link to experiment
If you would like to know how the interference pattern looks like in a real experiment, look at the Double-Slit Experiment.