A Penguin Watching a Fish Swim under the Ice
Task number: 2328
A penguin is watching a small fish which swims in the depth of \(2 \mathrm{m}\) under the surface. How deep does the fish seem to be when observed by the penguin? Water is frozen to the depth of \(40 \mathrm{cm}\)?
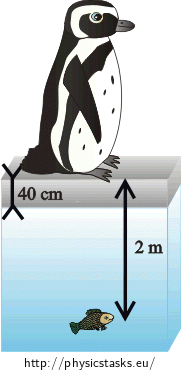
Note: we will assume that the penguin looks at the fish directly from above.
Notation
\(d=2 \mathrm{m}\) depth in which the fish swims \(t=40 \mathrm{cm}=0{,}4 \mathrm{m}\) thickness of the frozen surface \(x= ?\) depth in which the penguin sees the fish Hint 1
Draw a picture showing how the light ray goes from the fish into the eye of the penguin. In the picture we draw a penguin watching the fish not directly from above to see the refraction of the light ray on the water-ice and water-air boundaries. Mark in the picture where the penguin will see the fish (its virtual image).
Formulate Snell’s law for the two boundaries.
Hint 2
The apparent depth where the fish is can be determined when we draw right-angled triangles in the image. At first, express \(\mathrm{tg}\,{α}\), \(\mathrm{tg}\,{β}\) a \(\mathrm{tg}\,{γ}\) from the image. Write the relation for \(\mathrm{tg}\,{α}\) in two possible ways.
Hint 3
We apply the paraxial approximation.
Hint 4
We have derived all the necessary relations. Determine the depth \(x\) in which the penguin sees the fish from them.
Complete solution
Law of refraction
We draw an image showing how the light ray goes from the fish into the eye of the penguin. In the picture we draw a penguin watching the fish not directly from above to see the refraction of the light ray on the water-ice and water-air boundaries. Mark in the picture where the penguin will see the fish (its virtual image).
The light ray goes from the fish and it is incident on the ice layer at the angle \(γ\) where it is refracted and it is incident on the ice surface where it is again refracted and it continues into the penguin’s eye at the angle of incidence \(α\). This ray obeys the law of refraction. We can draw a virtual image of the fish in the depth \(x\) by elongating the ray incident on the penguin’s eye.
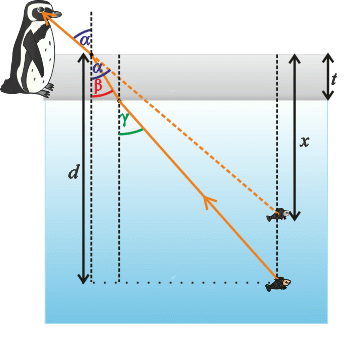
We write Snell’s law for the air-ice boundary: \[n_{1}\sin α=n_{2}\sin β,\tag{1}\] where \( n_{1}\) is the index of refraction of air and \(n_{2}\) is the index of refraction of ice.
Similarly, for the ice-water boundary it holds: \[n_{2}\sin β=n_{3}\sin γ,\tag{2}\] Where \(n_{3}\) is the index of refraction of water.
Comparing two previous relations we get: \[n_{1}\sin α=n_{3}\sin γ.\tag{3}\]
Using the paraxial approximation (see Hint 3), we can express the Snell’s law with the tangent function. It is important for us because we can express the tangents of angles \(α\), \(β\), \(γ\) from the image.
We rewrite the relations (1) a (3) using paraxial approximation: \[n_{1}\mathrm{tg}\, α=n_{2}\mathrm{tg}\, β,\tag{11}\] \[n_{1}\mathrm{tg}\, α=n_{3}\mathrm{tg}\, γ.\tag{12}\] (We did not rewrite the relation (2) because we will not use it in the following calculation.)
Expressing \(\mathrm{tg}\,{α}\), \(\mathrm{tg}\,{β}\) a \(\mathrm{tg}\,{γ}\)
We draw right-angled triangles in the image„Watching the fish“.
Let us denote:
\(p\) the distance between the normal for the air-ice boundary and the normal for the ice-water boundary.
\(q\) the distance between the ice-water boundary and the orthogonal projection of the fish on the water surface.
\(z\) is the distance between the water surface and intersection of the normal for ice-water boundary and the virtual light ray going to the virtual image of the fish.
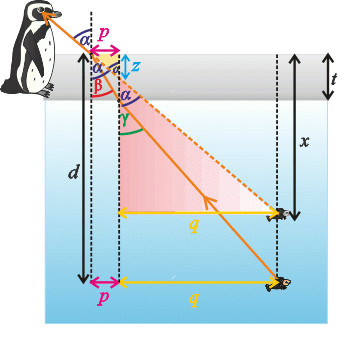
We can see from the yellow triangle that: \[\mathrm{tg}\, {α}=\frac{p}{z}. \tag{4}\] and from the red triangle we can derive: \[\mathrm{tg}\, {α}=\frac{q}{x−z}. \tag{5}\] 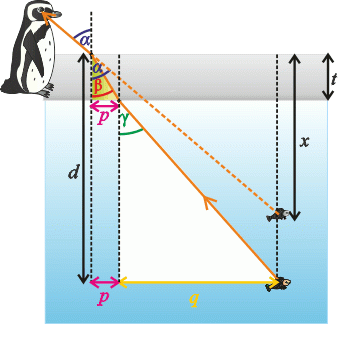
We can see from the green triangle that it holds: \[\mathrm{tg}\, {β}=\frac{p}{d}. \tag{6}\] and according to the white triangle we can write: \[\mathrm{tg}\, {γ}=\frac{q}{h−d}. \tag{7}\] Expressing the unknown depth \(x\)
We firstly use the relation (11). Looking at the relations above, we see that after substituting relations (4) and (6) into relation (11) and simplifying, the relation does not depend on \(p\) and we can express \(z\): \[n_{1}\mathrm{tg}\, α=n_{2}\mathrm{tg}\, β,\] \[n_{1}\frac{p}{z}=n_{2}\frac{p}{t}.\] We divide both sides of the equation by \(p\): \[n_{1}\frac{1}{z}=n_{2}\frac{1}{t}.\] We multiply both sides of the equation by \(\frac{z}{n_{2}}t\): \[\frac{n_{1}}{n_{2}}t=z.\] \[z=t\frac{n_{1}}{n_{2}}.\tag{13}\]
It is now convenient to use the relation (12) and substitute (5) and (7) into it: \[n_{1}\mathrm{tg}\, α=n_{3}\mathrm{tg}\, γ,\] \[n_{1}\frac{q}{x−z}=n_{3}\frac{q}{d−t}.\] Dividing by \(q\) we get an equation with only two unknowns (\(x\) and \(z\) which we want to determine). \[n_{1}\frac{1}{x−z}=n_{3}\frac{1}{d−t}.\] We now want to express the depth \(x\). Multiplying both sides of the equation by \(\left(x−z\right)\left(d−t\right)\) we get: \[n_{1}\left(d−t\right)=n_{3}\left(x−z\right).\] Expanding the bracket on the right side of the equation we get: \[n_{1}\left(d−t\right)=n_{3}x−n_{3}z.\] We add \(n_{3}z\) to both sides of the equation: \[n_{1}\left(d−t\right)+n_{3}z=n_{3}x.\] We divide the equation by \(n_{3}\): \[\frac{n_{1}}{n_{3}}\left(d−t\right)+z=x.\] We substitute for \(z\) from (13): \[x=\frac{n_{1}}{n_{3}}\left(d−t\right)+\frac{n_{1}}{n_{2}}d.\]
Numerical solution
We know from the task assignment:
\(d=2 \mathrm{m}\)
\(t=0{,}4 \mathrm{m}\)
We find the value of the index of refraction of air \(n_{1}\), ice \(n_{2}\) and water \(n_{3}\) :
\(n_{1}\) \(=\) \(1{,}00\)
\(n_{2}\) \(=\) \(1{,}31\)
\(n_{3}\) \(=\) \(1{,}33\)
Substituting we get:
\(x=\frac{n_{1}}{n_{3}}\left(d−t\right)+\frac{n_{1}}{n_{2}}t=\frac{1{,}00}{1{,}33}\left(2−0{,}4\right)+\frac{1{,}00}{1{,}31}\cdot 0{,}4 \mathrm{m} \dot= 1{,}51 \mathrm{m}.\)
Answer
The penguin sees the fish in the depth of \(1{,}51 \mathrm{m}\).






