Diffraction at a Grating
Task number: 1969
A grating with a groove period \(b\) having \(n\) slits in total is illuminated with light of wavelength \(\lambda\). A screen is positioned parallel with the grating at a discance \(L\).
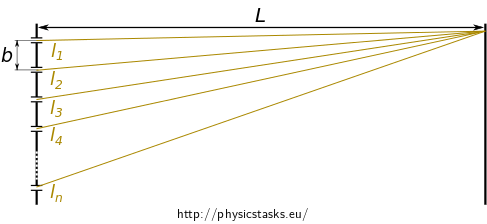
Assess the distribution of the light intensity on the screen, presuming that the slits are coherent sources of light with their width being much lower than their spacing. Assess the spacing of the maxima of the diffraction pattern.
- The slits are illuminated with a harmonic plane wave that is polarized along the direction of the slits and falls perpendicular onto the grating.
- Consider very narrow slits — so that the first minimim of diffraction of light at a single slit is far off the screen. In other words, presume that the illumination of the screen through one slit with the given screen distance and slit width would be uniform .
- Solve the task within the Fraunhofer approximation of diffraction, \(L\gg nb\).
This task is an extension of the task Young’s Interference Experiment, where just two slist are used. The result of the present task should condense to the same equations for \(n=2\).
Theory
- We use the complex representation of the electromagnetic wave in this task, which is introduced in detail in a related task. It is used also in the task Complex Representation and the Harmonic Plane Wave.
- We are supposed to solve the task within the approximation of Fraunhofer diffraction, i.e. at a very distant screen. This condition allows us to make several helpful simplifications during the calculation.
- There occurs no change of the polarization (direction of the electric field vector) of the incident light for its polarization being directed along the slits. It is thus enough to solve the equations for the magnitude of the electric field.
- The slits are very narrow, we presume that the illumination of the screen from a single slit would be uniform. We thus consider the slits to be linear sources of cylindrical waves. The electric field of one cylindrical wave at distance \(r\) from its source slit is \[E_\mathrm{cyl}(t,r) = \frac{\mathcal{E}_0}{\sqrt{r}} e^{i(\omega t - kr )},\] where \(\mathcal{E}_0\) is a quantity related to the intensity of light falling at the slit and to the width of the slit.
- At a large distance, the cylindrical waves can be locally assumed to be planar and the intensity of light of the resulting electric field can be calculated using the simple formula for plane waves: \[I = \frac{1}{2z_0} EE^*, \] where asterisk means the complex conjugate and \(z_0 = \sqrt{\frac{\mu_0}{\varepsilon_0}}\) is the impedance of vacuum.
- One can approximate, for small angles \(\delta \ll 1\), that \[\sin\delta \,\approx\, \tan \delta .\]
Hint 1 — Superposition of electric field
Draw a picture of the situation near to the grating and indicate the path differencesfor waves falling onto the screen from individual slits. Calculate the electric field generated by the sum of the waves with paths \(l_1,l_2\) to \(l_n\).
Afterwards, write down the complex conjugate of the resulting electric field \(E^\star\).
Hint 2 — Light intensity on the screen
Calculate the dependence of the intensity of light on the angle \(\alpha\) from the following formula
\[I = \frac{1}{2z_0} EE^\star,\]by using the calculated electric field and its complex conjugate.
Hint 3 — Separation of major maxima
Assess the distance between the major interference maxima on the screen for small angles \(\alpha\).
Determine the dependence of the spacing of the maxima on \(L, \, \lambda\) and \(b\).
Solution
As the screen is far away enough from the grating, we approximate all the factors \(\sqrt{l_i}\) of the decrease of the magnitude with a constant value \(\sqrt{L}\).
The electric field of the wave coming from the 1st, 2nd, to nth slit at a given point at the screen that is at a distance \(l_1,l_2\) to \(l_n\), respectively, from these slits, is:
\[ \begin{eqnarray} E_1 &=& \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)},\\ E_2 &=& \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_2)},\\ &\vdots& \\ E_n &=& \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_n)}. \end{eqnarray} \]The resulting field at a given point at the screen is directly the sum of these fields, because they are all in the same polarization state:
\[E = E_1 + E_2 + \ldots + E_n = \frac{\mathcal{E}_0}{\sqrt{L}} \left( e^{i(\omega t - kl_1)} + e^{i(\omega t - kl_2)} + \ldots + e^{i(\omega t - kl_n)} \right).\]We factor out the exponents (phases) of time and of the distance to the first slit:
\[=\frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \big(e^{-ik(\overbrace{l_1-l_1}^{\mathrm{def.\,}\Delta l_1})} + e^{-ik(\overbrace{l_2-l_1}^{\mathrm{def.\,}\Delta l_2})} + \ldots + e^{-ik(\overbrace{l_n-l_1}^{\mathrm{def.\,}\Delta l_n})} \big)\] and we symbolically sum the path differences: \[= \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \big(e^{-ik \Delta l_1} + e^{-ik \Delta l_2} + \ldots + e^{-ik \Delta l_n} \big)=\] \[= \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \sum_{j=1}^{n} e^{-ik \Delta l_j}. \tag{4}\]Let us now focus on the result of the summation. We express the path difference of the \(j\)th wave with respect to the first slit using a multiple of the groove period \(b\) an angle \(\alpha\).
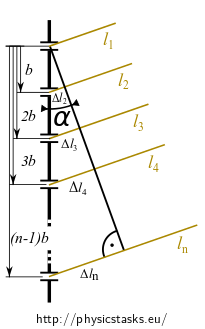
We draw perpendiculars from the first slit to the wave paths. For a far-enough screen, we can consider the paths from different slits to be parallel and all the angles \(\alpha\) to be the same.
It then holds that
\[\sin \alpha = \frac{\Delta l_j}{(j-1) \cdot b}\]and the path difference for the \(j\)th slit is:
\[\Delta l_j = (j-1) \, b \, \sin\alpha.\]Upon substituting into Equation (4), we get
\[E = \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \sum_{j=1}^{n} e^{-ik (j-1)b\sin\alpha}.\]We can see, that we are summing the \(n\) first terms of a geometric series with the first term \(1\) and the common ratio \(e^{-ikb\sin\alpha}\). We perform the summation:
\[E = \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \sum_{j=1}^{n} \big(\underbrace{e^{-ik b\sin\alpha}}_{\mathrm{kvocient}}\big)^{j-1} = \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \frac{\left(e^{-ikb\sin\alpha}\right)^n - 1 }{e^{-ikb\sin\alpha} - 1}.\]And we get the resulting electric field after a simple arrangement:
\[E = \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \frac{e^{-inkb\sin\alpha} - 1 }{e^{-ikb\sin\alpha} - 1}.\]The complex conjugate of the resulting electric field is then:
\[E^\star = \frac{\mathcal{E}_0}{\sqrt{L}} e^{-i(\omega t - kl_1)} \frac{e^{inkb\sin\alpha} - 1 }{e^{ikb\sin\alpha} - 1}.\]We use the calculated electric field and the formula for the intensity of light:
\[ I = \frac{1}{2z_0}EE^\star = \frac{\mathcal{E}_0^2}{2z_0 L} \underbrace{e^{i(\omega t - kl_1)}e^{-i(\omega t - kl_1)}}_{1} \frac{\big(e^{-inkb\sin\alpha} - 1\big)\big(e^{inkb\sin\alpha} - 1\big)} {\big(e^{-ikb\sin\alpha} - 1\big)\big(e^{ikb\sin\alpha} - 1\big)}. \]There are have similar expressions in the numerator and in the denominator in the fraction above. Let us process an equivalent expression with a general imaginar exponent \(\xi\) separately:
\[ \color{MidnightBlue}{ (e^{-i\xi} - 1)(e^{i\xi} - 1) = \underbrace{e^{-i\xi}e^{i\xi}}_{1} - e^{-i\xi} - e^{i\xi} + 1 = 2 - (e^{-i\xi} + e^{i\xi})= \\ = 2 - (\cos \xi - i \sin \xi + \cos \xi + i \sin \xi) = 4\frac{1-\cos \xi}{2} = 4 \sin^2 \frac{\xi}{2}. } \]With the particular exponents in the numerator and in the denominator of the fraction in function \(I\), we obtain:
\[ I = \frac{\mathcal{E}_0^2}{2z_0 L} \frac {\big(e^{-inkb\sin\alpha} - 1\big)\big(e^{inkb\sin\alpha} - 1\big)} {\big(e^{-ikb\sin\alpha} - 1\big)\big(e^{ikb\sin\alpha} - 1\big)} = \frac{\mathcal{E}_0^2}{2z_0 L} \frac {\sin^2 \frac{nkb\sin\alpha}{2}} {\sin^2 \frac{kb\sin\alpha}{2}}. \]We plot the dependence \(I=I(\sin\alpha)\)
\[ I = \frac{\mathcal{E}_0^2}{2z_0 L} \frac{\sin^2 \frac{nkb\sin\alpha}{2}}{\sin^2 \frac{kb\sin\alpha}{2}}. \tag{5}\]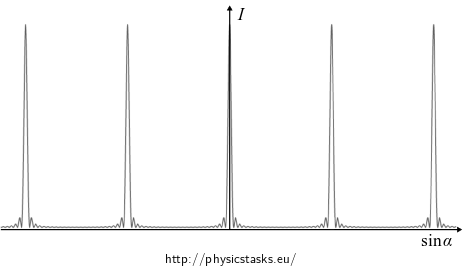
We observe a series of sharp maxima on the screen.
For small values of the angle, \(\alpha \ll 1\), one can approximate:
\[\sin\alpha \,\approx\,\tan \alpha = \frac{x}{L},\]where \(\alpha\) is the inclination of the rays from the normal to the screen.
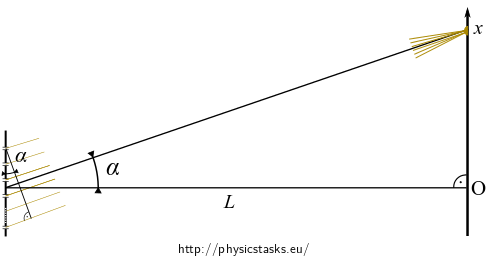
Equation (5) yields after subtituting \(\sin \alpha\) with \(\frac{x}{L}\) :
\[I = \frac{\mathcal{E}_0^2}{2z_0 L} \frac{\sin^2 \frac{nkbx}{2L}}{\sin^2 \frac{kbx}{2L}}.\tag{6}\]Let us assess the separation of the major maxima of the interference pattern. The periodic function in the denominator of the interference formula (6) is modulated with the “fast” function in the numerator that produces a large number (proportional to \(n\)) of minor interference maxima.
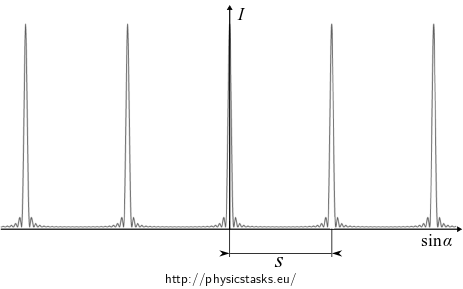
The maxima of the intensity of light occur when the denominator function tends to zero, which is when its argument is an integer multiple of \(\pi\). The separation \(s\) of the major maxima along the \(x\) axis is thus:
\[\frac{kbs}{2L} = \pi \qquad \Rightarrow \qquad s=\frac{2L\pi}{kb}=\frac{\lambda L}{ b},\]where \(k=\frac{2\pi}{\lambda}\).
The separation of the major maxima is:
\[s=\frac{\lambda L}{b}.\]The interference pattern widens with increasing distance \(L\) of the screen from the grating and with increasing wavelength \(\lambda\) of the interfering light and it narrows with increasing grating parameter \(b\).
Answer
The layout of the light intensity in the approximation of a very distant screen is:
\[I = \frac{\mathcal{E}_0^2}{2z_0 L} \frac{\sin^2 \frac{nkb\sin\alpha}{2}}{\sin^2 \frac{kb\sin\alpha}{2}},\]where \(\alpha\) is the angle formed between the path of the interfering waves from the grating to the given point at the screen and the normal to the screen.
The function \(I=I(\sin\alpha)\) can be plotted as follows:

The above plotted layout of the intensity of light describes well the central part of the screen. A decrease of the intensity of the maxima with increasing distance from the middle of the screen would occur with slits of finite width due to diffraction of light at individual slits.
The relation between the separation of the major maxima and the other parameters of the experiment is:
\[s \,\approx\, \frac{\lambda L}{b}.\]The interference pattern widens with increasing distance \(L\) of the screen from the grating and with increasing wavelength \(\lambda\) of the interfering light and it narrows with increasing grating parameter \(b\).
Comment — Finite intensity at the maxima
It may seem strange that the intensity pattern given by the function
\[I = \frac{\mathcal{E}_0^2}{2z_0 L} \frac{\sin^2 \frac{nkb\sin\alpha}{2}}{\sin^2 \frac{kb\sin\alpha}{2}}.\]yields finite values everywhere.

Why does not the intensity rise to infinity for \(\sin\alpha \to 0\) which renders a zero in the denominator?
In fact, it is not possible to inspect the behavior of the denominator of a fraction without looking at the numerator. The numerator also tends to zero for the same values of \(\alpha\) and one has to inspect the limit behavior of the fraction as a whole. In mathematical language:
\[\small \lim_{\xi \to 0} {\frac{\sin^2{n\xi}}{\sin^2 \xi}} = \lim_{\xi \to 0} \left({\frac{\sin {n\xi}}{n\xi}} \frac{n\xi}{\sin \xi}\right)^2 = n^2 \left( \underbrace{\lim_{\xi \to 0}\frac{\sin {n\xi}}{n\xi}}_{1} \cdot \underbrace{\lim_{\xi \to 0}\frac{\xi}{\sin {\xi}}}_{1} \right)^2 = n^2. \]And in our particular case:
\[ I_0 = \lim_{\sin\alpha\to 0} I = \frac{\mathcal{E}_0^2}{2z_0 L} \lim_{\sin\alpha\to 0} \frac{\sin^2 \frac{nkb\sin\alpha}{2}}{\sin^2 \frac{kb\sin\alpha}{2}} = \frac{\mathcal{E}_0^2}{2z_0 L}n^2 \]The intensity at the major maxima is indeed finite. It grows with the amplitude of the incident wave and with the number of illuminated slits and decreases with the distance to the screen.


