Collection of Solved Problems in Physics

Positive Meniscus Lens

Task number: 2216

A positive meniscus lens made from glass of refraction index \(1{,}5\) is in the air and its focal length is \(12 \mathrm{cm}\).

What are the radii of curvature of the two optical surfaces of the lens if the radius of curvature of the concave surface is two time greater than the radius of curvature of the convex surface?

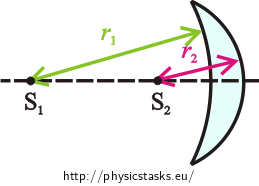
• Notation

  \(n_{g}=1{,}5\)	refraction index of glass
  \(f=12 \mathrm{cm}=0{,}12 \mathrm{m}\)	focal length
  \(r_{1}= ?\)	curvature radius of the concave surface
  \(r_{2}= ?\)	curvature radius of the convex surface

• Hint 1

  We read in the task assignment that the radius of the convex surface is two times greater than the radius of the concave surface. Write it down. Use the sign convention mentioned in Imaging a Bat by a Spherical Mirror and a Converging Lens, Radius of curvature and focal length and decide if the radii of curvature are positive or negative.

• Hint 1 solution

  We know from the sign convention that if the centre of curvature of the first surface is in front of the lens, its radius of curvature is negative. If the centre of curvature of the first surface is behind the lens, its radius of curvature is positive. Conversely for the second surface. Thus for the lens from the assignment it holds that the concave surface (first) has negative radius of curvature \(r_{1}\lt 0\) and convex surface (second) has positive radius of curvature \(r_{2}\gt 0\). As mentioned above, radius of concave surface is two times greater than radius of convex surface. We thus can write:

  \[r_{1}=−2r_{2}.\tag{1}\]

• Hint 2

  Radii of curvature of the optical surfaces of the lens determine the properties of the lens. They also change the focal length of the lens.

  Do you know any equation which describes the relation between a focal length of a lens and the radii of curvature of its surfaces?

  We will assume to have a thin lens.

• Hint 2 solution

  The relation between a focal length of a lens \(f\) and the radii of curvature of its surfaces \(r_{1}\) a \(r_{2}\) is described by Lensmaker’s equation. Let us write it for our thin lens: \[\frac{1}{f}=\left(\frac{n_{g}}{n_{a}}−1\right)\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}\right),\tag{2}\] where \(n_{g}\) is the refraction index of glass and \(n_{a}\) is the refraction index of air.

• Hint 3

  We can now use the relations which we found and determine the unknown radii of curvature.

• Hint 3 solution

  Let us revise the relations: \[r_{1}=−2r_{2},\tag{1}\] \[\frac{1}{f}=\left(\frac{n_{g}}{n_{a}}−1\right)\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}\right).\tag{2}\]

  We substitute relation (1) into equation (2): \[\frac{1}{f}=\left(\frac{n_{g}}{n_{a}}−1\right)\left(\frac{1}{\left(−2r_{2}\right)}+\frac{1}{r_{2}}\right).\]

  We will simplify the equation to express the radius of curvature \(r_{2}\).

  Firstly, let us simplify the fractions in brackets: \[\frac{1}{f}=\left(\frac{n_{g}−n_{a}}{n_{a}}\right)\left(\frac{−1}{2r_{2}}+\frac{2}{2r_{2}}\right),\] \[\frac{1}{f}=\left(\frac{n_{g}−n_{a}}{n_{a}}\right)\left(\frac{1}{2r_{2}}\right).\]

  We multiply both sides of the equation by \(\frac{n_{a}}{n_{g}−n_{a}}\): \[\frac{1}{f}\frac{n_{a}}{n_{g}−n_{a}}=\frac{1}{2r_{2}}.\] We multiply both sides of the equation by two: \[\frac{2}{f}\frac{n_{a}}{n_{g}−n_{a}}=\frac{1}{r_{2}},\] \[\frac{2n_{a}}{f\left(n_{g}−n_{a}\right)}=\frac{1}{r_{2}}.\]

  We express \(r_{2}\): \[r_{2}=\frac{f\left(n_{g}−n_{a}\right)}{2n_{a}}.\]

  We expressed the radius of curvature of the convex surface. We will calculate the radius of curvature of the second surface using (1): \[r_{1}=−2r_{2},\] \[r_{1}=−2\cdot \frac{f\left(n_{g}−n_{a}\right)}{2n_{a}}.\]

  Thus : \[r_{1}= \frac{f\left(n_{a}−n_{g}\right)}{n_{a}}.\]

  Numerical solution

  We know from the task assignment that:

  \(n_{g}=1{,}5\) (refraction index of glass)

  \(f=12 \mathrm{cm}=0{,}12 \mathrm{m}\) (focal length of the lens)

  We find the refraction index of air in tables:

  \(n_{a}=1{,}0\)

  Substituting into the relation for the radius of curvature of the concave surface we get:

  \(r_{1}= \frac{f\left(n_{a}−n_{g}\right)}{n_{a}}=\frac{0{,}12\cdot \left(1−1{,}5\right)}{1} \mathrm{m}=−0{,}06 \mathrm{m}=−6 \mathrm{cm}\).

  Substituting into the relation for the radius of curvature of the convex surface gives us:

  \(r_{2}=\frac{f\left(n_{g}−n_{a}\right)}{2n_{a}}=\frac{0{,}12\cdot \left(1{,}5−1\right)}{2{\cdot} 1 }=0{,}03 \mathrm{m}=3 \mathrm{cm}\).

  We calculated the radius of curvature of the concave surface to be negative and the radius of curvature of the convex surface to be positive as we expected from the sign convention.

• Complete solution

  Sign convention

  We know from the sign convention mentioned in Imaging a Bat by a Spherical Mirror and a Converging Lens, Radius of curvature and focal length that if the centre of curvature of the first surface is in front of the lens, its radius of curvature is negative. If the centre of curvature of the first surface is behind the lens, its radius of curvature is positive. Conversely for the second surface. Thus for the lens from the assignment it holds that the concave surface (first) has negative radius of curvature \(r_{1}\lt 0\) and convex surface (second) has positive radius of curvature \(r_{2}\gt 0\). As mentioned above, radius of concave surface is two times greater than radius of convex surface. We thus can write: \[r_{1}=−2r_{2}.\tag{1}\]

  Lensmaker’s equation

  Radii of curvature of the optical surfaces of the lens determine the properties of the lens. They also change the focal length of the lens.

  The relation between a focal length of a lens \(f\) and the radii of curvature of its surfaces \(r_{1}\) a \(r_{2}\) is described by Lensmaker’s equation. Let us write it for our thin lens: \[\frac{1}{f}=\left(\frac{n_{g}}{n_{a}}−1\right)\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}\right),\tag{2}\] where \(n_{g}\) is the refraction index of glass and \(n_{a}\) is the refraction index of air.

   

  Curvature radii

  We can now use the relations which we found and determine the unknown radii of curvature.

  We substitute relation (1) into equation (2) \[\frac{1}{f}=\left(\frac{n_{g}}{n_{a}}−1\right)\left(\frac{1}{\left(−2r_{2}\right)}+\frac{1}{r_{2}}\right).\]

  We will simplify the equation to express the radius of curvature \(r_{2}\).

  Firstly, let us simplify the fractions in brackets: \[\frac{1}{f}=\left(\frac{n_{g}−n_{a}}{n_{a}}\right)\left(\frac{−1}{2r_{2}}+\frac{2}{2r_{2}}\right),\] \[\frac{1}{f}=\left(\frac{n_{g}−n_{a}}{n_{a}}\right)\left(\frac{1}{2r_{2}}\right).\]

  We multiply both sides of the equation by \(\frac{n_{a}}{n_{g}−n_{a}}\): \[\frac{1}{f}\frac{n_{a}}{n_{g}−n_{a}}=\frac{1}{2r_{2}}.\] We multiply both sides of the equation by two: \[\frac{2}{f}\frac{n_{a}}{n_{g}−n_{a}}=\frac{1}{r_{2}},\] \[\frac{2n_{a}}{f\left(n_{g}−n_{a}\right)}=\frac{1}{r_{2}}.\] We express \(r_{2}\): \[r_{2}=\frac{f\left(n_{g}−n_{a}\right)}{2n_{a}}.\]

  We expressed the radius of curvature of the convex surface. We will calculate the radius of curvature of the second surface using (1): \[r_{1}=−2r_{2},\] \[r_{1}=−2\cdot \frac{f\left(n_{g}−n_{a}\right)}{2n_{a}}.\] Thus : \[r_{1}= \frac{f\left(n_{a}−n_{g}\right)}{n_{a}}.\]

  Numerical solution

  We know from the task assignment that:

  \(n_{g}=1{,}5\) (refraction index of glass)

  \(f=12 \mathrm{cm}=0{,}12 \mathrm{m}\) (focal length of the lens)

  We find the refraction index of air in tables:

  \(n_{a}=1{,}0\)

  Substituting into the relation for the radius of curvature of the concave surface we get:

  \(r_{1}= \frac{f\left(n_{a}−n_{g}\right)}{n_{a}}=\frac{0{,}12\cdot \left(1−1{,}5\right)}{1} \mathrm{m}=−0{,}6 \mathrm{m}=−6 \mathrm{cm}\).

  Substituting into the relation for the radius of curvature of the convex surface gives us:

  \(r_{2}=\frac{f\left(n_{g}−n_{a}\right)}{2n_{a}}=\frac{0{,}12\cdot \left(1{,}5−1\right)}{2{\cdot} 1 }=0{,}3 \mathrm{m}=3 \mathrm{cm}\).

  We calculated the radius of curvature of the concave surface to be negative and the radius of curvature of the convex surface to be positive as we expected from the sign convention.

• Answer

  The radius of curvature of the concave surface of the lens is \(r_{1}=6 \mathrm{cm}\) and the radius of curvature of the convex surface is \(r_{2}=3 \mathrm{cm}\).

• Thick lens

  We can write the Lensmaker’s equation for thick lens of the thickness \(d\) as follows: \[\frac{1}{f}=\left(\frac{n_{g}}{n_{a}}−1\right)\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}\right)−\frac{\left(\frac{n_{g}}{n_{a}}−1\right)^2 d}{\frac{n_{g}}{n_{a}}r_{1}r_{2}}.\]

  If the thickness of a lens is very small compared to the radii of curvature of the lens surfaces, we can neglect it, assume that \(d=0\). In this case Lensmaker’s equation for thick lens becomes Lensmaker’s equation for thin lens which we mentioned in hint 2: \[\frac{1}{f}=\left(\frac{n_{g}}{n_{a}}−1\right)\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}\right).\] Thin lens is a frequently used approximation of a thick lens.

   

  We can also determine how the properties of the lens would change if we did not neglect its thickness.

  We know that our lens has radii of curvature  \(r_{1}=−6 \mathrm{cm}\) and \(r_{2}=3 \mathrm{cm}\).

  We can calculate the focal length f from the Lensmaker’s equation for thin lens:

  \(\frac{1}{f}=\left(\frac{n_{g}}{n_{a}}−1\right)\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}\right)=\left(\frac{1{,}5}{1}−1\right)\left(\frac{1}{−6}+\frac{1}{3}\right) \mathrm{\frac{1}{cm}}=\left(0{,}5\right)\left(\frac{−1}{6}+\frac{2}{6}\right) \mathrm{\frac{1}{cm}}=\frac{1}{12} \mathrm{\frac{1}{cm}},\)

  \(f=12 \mathrm{cm}\).

  We will now calculate the focal length f from the equation for thick lens. We will assume the thickness to be for example \(d=1 \mathrm{cm}\):

  \(\frac{1}{f}=\left(\frac{n_{g}}{n_{a}}−1\right)\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}\right)−\frac{\left(\frac{n_{g}}{n_{a}}−1\right)^2 d}{\frac{n_{g}}{n_{a}}r_{1}r_{2}}=\left(\frac{1}{12}−\frac{\left(\frac{1{,}5}{1}−1\right)^2 {\cdot}1}{\frac{1{,}5}{1}\left(−6\right)\cdot 3}\right) \mathrm{\frac{1}{cm}}= \left(\frac{1}{12}+\frac{\left(0{,}5\right)^2}{1{,}5{\cdot} 18}\right) \mathrm{\frac{1}{cm}} = \left(\frac{1}{12}+\frac{1}{12{\cdot} 9} \mathrm{\frac{1}{cm}} =\frac{5}{54}\right) \mathrm{\frac{1}{cm}},\)

  \(f=\frac{54}{5} \mathrm{cm}=10{,}8 \mathrm{cm}\).

  We see that the focal lengths of thin and thick lens are different. Thus, it is necessary to consider in every case if we can neglect the thickness or not.