Delayed Sunset
Task number: 1968
An observer watches the sunset from the surface of the Earth. Due to refraction of light on the interface of vacuum (the free space) and atmosphere, the observer sees the Sun set later than it would be without the atmosphere.
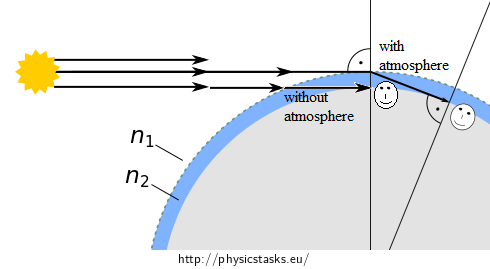
The real interface of vacuum and atmosphere is not sharp. Use a simplifying model according to the figure above. Consider a single spherical interface of two isotropic media: vacuum (\(n_1=1\)) and idealised atmosphere (\(n_2=1.0003\)), with such a thickness that the Sun rays fall at right angle at the interface.
Hint 1 – Sketch the situation
Draw a picture showing the moment of the sunset as observed from the surface of the Earth. Assess the angles of incidence and refraction of the Sun rays at the interface of vacuum and atmosphere.
Keep in mind that the thickness of the atmosphere is just a small fraction of the Earth radius.
Hint 2 — Refraction angle
What is the relation between the angles of incidence and refraction? Remind Snell’s law.
Hint 3 — Time delay
- From what point would the observer see the sunset if there was no atmosphere (no interface)?
- What angle does the Earth need to rotate to take the observer from the hypothetical point of observation of sunset without atmosphere to the actual point of observation?
- What time does it take the Earth to rotate by this angle?
Solution
We draw the described situation. The observer at point A sees that the Sun is just setting behind the observer’s horizon. The Sun rays refract at the interface of atmosphere and vacuum at point P.
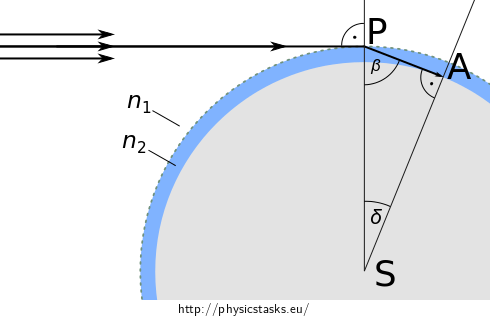
The angle of incidence in the latest moment when the Sun rays refract towards the observer is \(\frac{\pi}{2}\) at point P, the angle of refraction is denoted \(\beta\).
Snell’s law for the vacuum–air interface is:
\[n_1 \sin\frac{\pi}{2} = n_2 \sin \beta.\]We express the angle of refraction:
\[\beta = \arcsin \frac{n_1}{n_2} .\tag{2}\]If there was no atmosphere, the observer would see the Sun setting behind the horizon at the moment when the observer was at point P. The Earth rotated by the angle \(\delta\) from that moment to the moment when the observer is at the point of the actual observation of the sunset (point A).
\[\delta = \frac{\pi}{2} - \beta.\]We express the angular velocity \(\omega\) of Earth rotation as the ratio of the full angle \(2\pi\) and the period of Earth rotation \(T\). The time of rotation by angle \(\delta\) is:
\[t = \frac{\delta}{\omega} = \frac{\frac{\pi}{2} - \beta}{\frac{2\pi}{T}}.\]We get the final formula upon substituting of the angle \(\beta\) from Equation (2) and arranging of the formula:
\[t = \frac{1}{2\pi} \left[\frac{\pi}{2} - \arcsin \left(\frac{n_1}{n_2} \right)\right]T.\]With given numerical values, we get:
\[ t = \frac{1}{2\pi} \left[\frac{\pi}{2} - \arcsin \left(\frac{1}{1.0003} \right)\right]24{\cdot} 60~\mathrm{min} \doteq 5.6~\mathrm{min}. \]Comment
The assignment supposes a right angle at point P which makes the task easy to calculate. However, this is an oversimplificaiton - the thickness of the atmosphere under these conditions would be less than \(2\,\mathrm{km}\). Nevertheless, the task gives a good estimate of the delay.
In reality, the Sun rays do not undergo only a single refraction. The index of refraction of the atmosphere changes smoothly from 1 (vacuum) to 1.0003 (at the sea level) and the Sun rays are refracted bit by bit accordingly, resultin in a smooth “bend”. The actual delay of the sunset is about 2 minutes, the sunrise is some 2 minutes advanced symmetrically and the light-day at the Earth is about 4 minutes longer than it would be without the atmosphere.
The trajectory of the gradually bending ray can be calculated numerically without complicated mathematics e.g. in a spreadsheet (Excel, Calc,...).
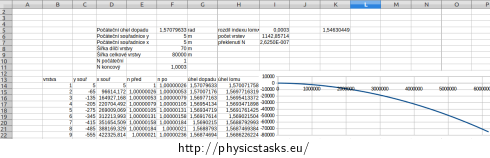
One can enter the initial and the final index of refraction, the initial coordinates, the angle of incidence, the width and number of model isotropic layers of the atmosphere as parameters and examine how does the trajectory of the rays depend on them.
Answer
Our simple model yields a delay of the sunset of about \(5.6\,\mathrm{min}\).


