Collection of Solved Problems in Physics

DVD as an Optical Grating

Task number: 1700

Edward, Eugene and Eve attended a laboratory lesson at school. They placed a DVD on a flat surface and pointed a laser with a wavelength of 650 nm to the DVD so that the ray was perpendicular to the DVD. First-order maxima appeared on a wall at a distance of 130 cm from the DVD and at a height of 70 cm. The figure below shows the arrangement of this experiment.

a) What is the distance between two adjacent recording tracks on the DVD?

b) How many tracks are there on 1 mm of length?

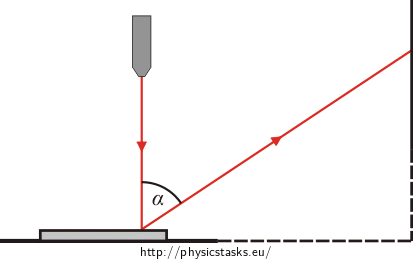
• Hint 1

  A DVD behaves like an optical grating. Do you know the relationship which applies for the path difference of rays?

• Solution of Hint 1

  In this task, the DVD acts as an optical grating which reflects light. This optical grating behaves almost the same as a grating through which the light passes. The only difference is that the diffraction phenomena occur on the same side of the grating where the light source is.

  For a path difference Δl of two adjacent rays the following applies

  \[\mathrm{Δ}l = \,b\sin\,α,\]

  where Δl is the path difference of the rays, b is a distance between two tracks on the DVD α is the deflection angle. We substitute a condition for a maximum Δl = kλ for Δl, where k is equal to 1 (from the assignment)

  We evaluate b and for angle α we substitute the relation from Hint 2.

  For detailed derivation see the task Deflection of the First Diffraction Maximum at a Grating.

• Hint 2

  Determine the deflection angle α of the first maximum using given distances.

• Solution of Hint 2

  

  From the picture we can see that

  \[\mathrm{tg}\,\,α=\,\frac{d}{x},\]

  where d is the distance between the DVD and the wall and x is the height of the first-order maximum on the wall.

• Given values

  d = 130 cm = 1.3 m	Distance between the DVD and the wall
  k = 1	Order of maximum
  λ = 650 nm = 6.5·10−7 m	Wavelength of light
  x = 70 cm = 0.7 m	Height of first-order maximum
  b = ? (nm)	Distance between two tracks on a DVD
  N = ?	Number of tracks per 1 mm of length

• Solution

  In this task, the DVD acts as an optical grating which reflects light. This grating behaves almost like a grating through which the light passes. The only difference is that the diffraction phenomena occur on the same side of the grating where the light source is.

  In this task we want to determine the distance of two tracks and how many tracks is there per 1 mm of length. For this calculation we need to know the relation for the deflection angle αand the relationship for the path difference Δl of the rays.

  

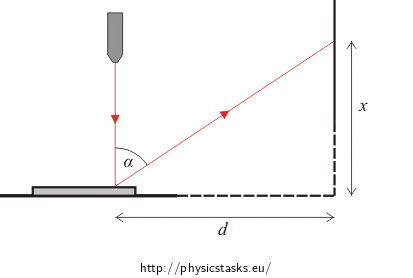
  From the picture we obtain a relationship:

  \[\mathrm{tg}\,\,α=\,\frac{d}{x},\]

  where d is the distance between the DVD and the wall and x is the height at which the first-order maxima appear.

  For the path difference Δl the following applies:

  \[\mathrm{Δ}l = \,b\sin\,α,\]

  where Δl is the path difference of the rays, b is the distance between two tracks on the DVD and α is the deflection angle.

  For Δl we substitute a condition for a maximum Δl = kλ, where k = 1.

  We evaluate the distance b:

  \[b=\,\frac{\mathrm{Δ}l}{\sin\,α}=\,\frac{λ}{\sin\,α}.\]

   

  Numerical substitution

  First, we calculate the angle using the equation:

  \[\mathrm{tg}\,\,α=\,\frac{d}{x}=\,\frac{1.3}{0.7}\,\dot=\,1.86 \quad\Rightarrow\quad α\,\dot=\,61.74°\]

  and then we calculate the distance b between two tracks

  \[b=\,\frac{6.5{\cdot}10^{−7}}{\sin\,61.74}\,\mathrm{m}\,\dot=\,7.40{\cdot}10^{−7}\,\mathrm{m}\,\dot=\,740\,\mathrm{nm}.\]

  Number of tracks N per 1 mm can be obtained as follows:

  \[N=\,\frac{10^{−3}\,\mathrm{m}}{b}=\,\frac{10^{−3}\,\mathrm{m}}{7.38{\cdot}10^{−7}}\,\dot=\,1400.\]

• Answer

  The distance between two tracks on a DVD is 740 nm and per 1 mm of length there are 1,400 tracks.

• Link to experiment

  In the experiment Diffraction on a CD you can find a detailed description of how to perform the experiment.