Optical Prism and a Mirror
Task number: 2215
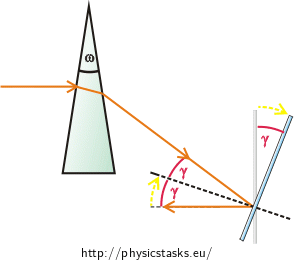
A horizontal light ray is incident on a prism. The index of refraction of the prism is 1,5 and its apex angle is 4°. After the light ray passes through the prism it is incident on a vertical mirror and is reflected there (see picture).
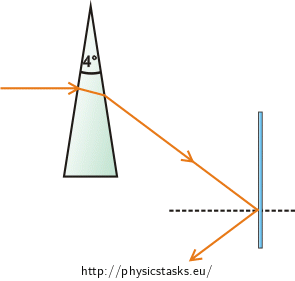
How much do we need to rotate the mirror when we want the light ray to move horizontally again after reflection?
Notation
\(ω=4\mathrm{°}\) apex angle \(n=1{,}5\) index of refraction of the prism \(γ= ?\) angle of rotation of the mirror Hint 1
Draw the picture from the task assignment again. Draw the ray which is reflected from the mirror horizontally. Consider how we need to rotate the mirror so that it reflects the ray in this way. Mark the angle of rotation of the mirror \(γ\) in the picture.
Hint 2
What does the term „angle of deviation“ mean in optics? What is the relation between the angle of deviation \(δ\) and the angle of rotation of the mirror \(γ\)?
Hint 3
We need to determine the angle of deviation \(\delta\). How is the angle of deviation \(\delta\) related to the apex angle ω?
Hint 4
Write the law of refraction for both boundaries (air-prism and prism-air).
Hint 5
We can simplify the law of refraction for both boundaries using the fact that the apex angle \(ω\) is very small.
Hint 6
Use relations (1), (5), (6), (9) and (10) to determine by what angle we must rotate the mirror.
Complete solution
Relation between the angle of rotation \(γ\) and the angle of deviation \(δ\)
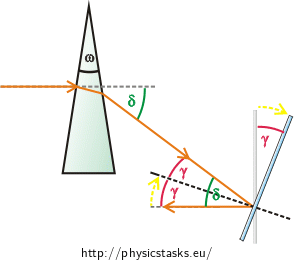
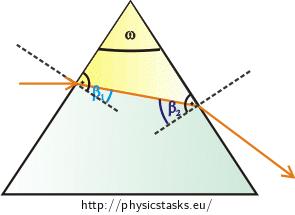
We draw the picture from the task assignment again. We draw the ray which is reflected from the mirror horizontally. We must rotate the mirror bearing in mind that the angle of incidence equals the angle of reflection (from the law of reflection). The mirror will be rotated around the point of incidence of the ray. We will mark in the picture how the normal (which passes through this point) and the mirror change their location when being rotated. The normal is always perpendicular to the mirror. Thus, if we rotate the mirror by an angle \(γ\), the normal is also rotated by the angle \(γ\).
Then we mark the so called „deviation angle“ \(δ\) in the picture (the angle which the light ray emerging from the prism forms with the incident ray). Relation between the angle of deviation \(δ\) and the angle of rotation of the mirror \(γ\) results from geometry (angles \(δ\) marked in the picture are alternate angles): \[δ=2γ.\tag{1}\]
Relation between the deviation angle and the apex angle \(ω\)
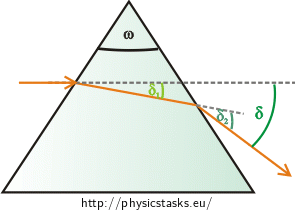
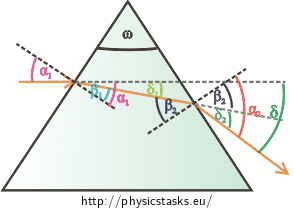
We will determine the relation between the angle of deviation \(δ\) and the apex angle \(ω\) step by step. It holds for the deviation angle that: \[δ=δ_{1}+δ_{2},\tag{2}\] where \(δ_{1}\) is the angle by which the ray is deviated when it enters the prism and \(δ_{2}\) is the angle by which the ray is deviated from its direction in the prism when the it emerges from the prism.
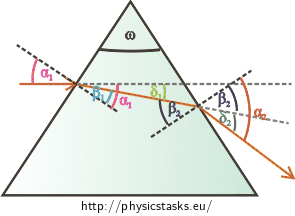
It holds for \(δ_{1}\) that: \[δ_{1}=α_{1}−β_{1},\tag{3}\] where \(α_{1}\) is the angle of incidence on the air-prism boundary and \(β_{1}\) is the angle of refraction on this boundary. Similarly, it holds for \(δ_{2}\) that: \[δ_{2}=α_{2}−β_{2},\tag{4}\] where \(β_{2}\) is the angle of incidence on the prism-air boundary and \(α_{2}\) is the angle of reflection on this boundary.
As the sum of the internal angles of triangle is \(180\mathrm{°}\) it holds that: \[ω+\left(90\mathrm{°}−β_{1}\right)+\left(90\mathrm{°}−β_{2}\right)= 180\mathrm{°}\] Simplifying the equation, we get: \[ω=β_{1}+β_{2}.\tag{5}\] We substitute relations (3) and (4) into relation (2): \[δ=δ_{1}+δ_{2},\] \[δ=α_{1}−β_{1}+α_{2}−β_{2}.\] We rewrite it: \[δ=α_{1}+α_{2}−\left(β_{1}+β_{2}\right).\] And substituting from (5) we gain the relation between \(δ\) and \(ω\): \[δ=α_{1}+α_{2}−ω.\tag{6}\]
Law of refraction and its simplification
Law of refraction for the air-prism boundary: \[n_{a}\sin{α_{1}}=n\sin{β_{1}},\tag{7}\] where \(n\) is the index of refraction of the prism and \(n_{a}\) is the index of refraction of air.
Law of refraction for the prism-air boundary: \[n_{a}\sin{α_{2}}=n\sin{β_{2}}.\tag{8}\]
We realise that when the apex angle \(ω\) is small, the angles \(α_{1}\), \(α_{2}\), \(β_{1}\) and \(β_{2}\) are also small. If we measure angles in radians, the value of sine of a small angle is approximately equal to size of this angle. Thus, we can rewrite the expressions (7) and (8) as follows: \[n_{a}α_{1}=nβ_{1},\tag{9}\] \[n_{a}α_{2}=nβ_{2}.\tag{10}\]
Angle of rotation of the mirror \(γ\)
Only the value of the apex angle \(ω\) and the index of refraction of the prism \(n\) are known from the task assignment. We can find the index of refraction of air \(n_{a}\) in tables. We want the angle \(γ\) to be dependent only on known physical quantities. We express the angles \(α_{1}\), \(α_{2}\) from (9) and (10): \[α_{1}=\frac{n}{n_{a}}β_{1},\tag{11}\] \[α_{2}=\frac{n}{n_{a}}β_{2}.\tag{12}\]
Let us first write the equation for the angle of deviation \(δ\).
We substitute the relations (11) and (12) in the relation (6): \[δ=\frac{n}{n_{a}}β_{1}+\frac{n}{n_{a}}β_{2}−ω.\] We factor out the fraction \(\frac{n}{n_{a}}\): \[δ=\frac{n}{n_{a}}\left(β_{1}+β_{2}\right)−ω.\] We substitute from (5) for the expression \(β_{1}+β_{2}\): \[δ=\frac{n}{n_{a}}ω−ω.\] We factor out \(ω\): \[δ=ω\left(\frac{n}{n_{a}}−1\right).\] We substitute from (1) into the equation: \[2γ=ω\left(\frac{n}{n_{a}}−1\right).\] Dividing both sides of equation by \(2\) we get: \[γ=\frac{ω}{2}\left(\frac{n}{n_{a}}−1\right).\]
Numerical solution
We know from the task assignment that:
\(ω= 4\mathrm{°}\)
\(n= 1{,}5\)
We know from the tables that:
\(n_{a}= 1\)
Thus:
\(γ=\frac{ω}{2}\left(\frac{n}{n_{a}}−1\right)=\frac{4\mathrm{°}}{2}\left(\frac{1{,}5}{1}−1\right)= 1\mathrm{°}.\)
Answer
We must rotate the mirror by \(1 \mathrm{°}\) clockwise.
Additional task
How would the situation change if we submerged the prism in water?
Link to an experiment
You can find an experiment in task Refraction of Monochromatic Light With a Prism which shows when the angle of deviation is minimal.