Diffraction at a Slit

Task number: 1970

A plane harmonic wave falls onto an infinitely long slit with width $d$. Presume a zero angle of incidence of the wave onto the slit and assess the intensity of light on a screen that is parallel to the aperture and lies at a distance $l$ from it. Plot the function of intensity on the screen and calculate the width of the maxima of the interference pattern.

Consider Fraunhofer approximation of diffraction, i.e. on a very distant screen.

Analysis
The infinitely long slit of given width can be modeled as a stripe of inifinitely long linear sources positioned continuously across the width of the slit.

The yellow line segment on the figure below presents the set of point intersections of the linear sources with the picture plane.

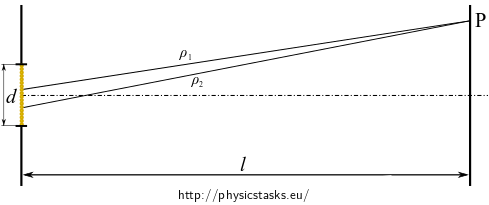
The electric field of a cylindrical wave can be described as:
\[E_\mathrm{cyl}(\rho) = \frac{\mathcal{E}_0}{\sqrt{\rho}}e^{i(\omega t - k\rho)},\]
where $\mathcal{E}_0$ is a magnitude constant related to the electric field of the incoming wave, $\rho$ is the radius of the wave in the cylidrical coordinates that have their origin at the given line source and $k=\frac{2\pi}{\lambda}$ is the wave number of the wave.

Cylindrical waves from different parts of the slit fall at a selected point P on the screen after passing along paths of different lengths $\rho$ and they interfere with each other. We find the resulting electric field as a superposition of the contributions from the linear sources over the whole width of the slit.

The wavefronts of the cylindrical waves can be considered approximately planar at the screen that is far enough. Then we can calculate the intensity of the resulting wave using the formula for a plane wave:
\[I = \frac{1}{2z_0} EE^\star,\]
where $E$ is the electric field of the resulting wave and $z_0 = \sqrt{\frac{\mu_0}{\varepsilon_0}}$ is the impedance of free space.

It follows from the nature of cylindrical waves that the intensity on the screen will show translational symmetry along the slit. We thus solve the task in the plane perpendicular to the slit axis.
Integral needed for the calculation
One needs to know how to integrate an exponential function with a multiplicative constant in the exponent:
\[\int e^{\varphi x}\,\mathrm{d}x = \frac{e^{\varphi x}}{\varphi} + C.\]
Hint 1 — Electric field
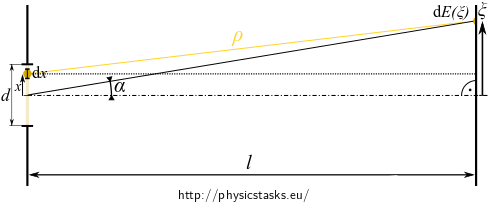
Write down the contribution to the electric field on the screen from an elementary linear source of infinitesimal width $\mathrm{d}x$ located at distance $x$ from the center of the slit (see the figure below).

Express the cylindrical radius $\rho$ (the ray path from the given linear source to the given point at the screen) using the screen distance $l$, the coordinate $x$ of the elementary source within the slit and the coordinate $\xi$ of the observation point on the screen. Arrange the expression taking into account that $x \lt d\ll l$.

The resulting electric field is given by the sum of the contributions from all elementary sources across the slit that we consider to be a narrow stripe of sources of cylindrical waves. These stripes cover continuously the width of the slit — write down the corresponding integral.
Hint 1 solution — Electric field
The contribution to the electric field on the screen at a point with coordinate $\xi$ from the elementary source of width $\mathrm d x$ located at the distance $x$ from the center of the slit is:
\[\mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{\rho}} e^{i(\omega t - k\rho)} \mathrm{d}x,\tag{1}\]
where $E_0$ is a constant ($[E_0]=\mathrm{V}\cdot\mathrm{m^{-\frac{3}{2}}}$) and $\rho$ is the ray path from the linear elementary source to the point at the screen that can be expressed using $l, \, \xi, \, x$ as follows:
\[\rho = \sqrt{l^2 + (\xi-x)^2}.\]
We implement two approximations:
1. Neglecting the decrease of amplitude across the screen:
  
  The amplitude of the electric field in (1) decreases with $\sqrt\rho$. For a screen far enough, the change of $\rho$ at various points along the $\xi$ coordinate is negligible and we approximate the variable expression $\frac{1}{\sqrt\rho}$ with the constant value $\frac{1}{\sqrt{l}}$, corresponding to the point at the optical axis. This simplifies the future integration.
2. We rearrange the expression for $\rho$ taking into account that $|x| \lt d \ll l$:
  \[\rho = \sqrt{l^2 + (\xi-x)^2} = \sqrt{l^2 + \xi^2 - 2\xi x + x^2} = \\ = \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{grey}{\frac{x^2}{l^2 + \xi^2}}}= \]
  We drop the grey fraction above as it is negligible for large $l$ with respect to the first fraction. Instead, we insert a negligibly small addition (in blue below) to complete the square of the expression inside the square root:
  \[ \begin{align} &= \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{blue}{\frac{\xi^2 x^2}{\left(l^2 + \xi^2\right)^2}}}= \\ &= \sqrt{l^2 + \xi^2}\bigg(1-\frac{\xi x}{l^2 + \xi^2} \bigg)= \\ &= \sqrt{l^2 + \xi^2}-x\overbrace{\frac{\xi}{\sqrt{l^2 + \xi^2}}}^{\sin \alpha} \\ &= \sqrt{l^2 + \xi^2} - x\sin \alpha. \end{align} \]
The approximations above give us the electric field contribution in the following shape:
\[ \mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{l}} e^{i(\omega t - k\rho)}\mathrm{d}x, \qquad \mathrm{with} \, \rho = \sqrt{l^2 + \xi^2} - x\sin \alpha. \]
The resulting electric field at the coordinate $\xi$ at the screen is given by the sum of the electric field contributions from all elementary sources over the slit width from $x=-\frac{d}{2}$ to $\frac{d}{2}$:
\[ E(\xi) = \int_\mathrm{slit}\mathrm{d}E_x(\xi) = \int_{-\frac{d}{2}}^{\frac{d}{2}} \frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x. \]
Hint 2 — Integrating the electric field
Solve the integral found in the previous Hint solution:
\[E(\xi) = \int_{-\frac{d}{2}}^{\frac{d}{2}} \frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x. \]
By this integration, we “sum up” the contributions of the electric field from the elementary sources in the slit at point $\xi$ on the screen

Itemize the exponential into a product of elementary exponential functions, factor out the terms independent of the integration variable $x$ in front of the integral. There remains a simple integral of the form:
\[A \int e^{\varphi x}\,\mathrm{d}x = A \frac{e^{\varphi x}}{\varphi} + C .\]
Assess the complex conjugate $E^\star(\xi)$ of the obtained function $E(\xi)$.
Hint 2 solution — Integrating the electric field
We factor out the terms independent of $x$ in front of the integral:
\[ \begin{align} E(\xi) &= \int_{-\frac{d}{2}}^{\frac{d}{2}} \frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x = \\ &= \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \int_{-\frac{d}{2}}^{\frac{d}{2}} e^{ikx\sin \alpha}\,\mathrm{d}x = \\ &= \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left[ \frac{e^{ikx\sin \alpha}}{ik\sin\alpha} \right]_{-\frac{d}{2}}^{\,\,\frac{d}{2}} = \\ &= \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left(e^{ik\frac{d}{2}\sin \alpha} - e^{-ik\frac{d}{2}\sin \alpha} \right). \end{align} \]
Let us abbreviate $\psi = k\frac{d}{2}\sin \alpha$. We separately treat the complex exponentials in the parentheses. We transform them to the trigonometric shape $(e^{i\varphi} = \cos \varphi + i \sin \varphi)$.
\[e^{i\psi} - e^{-i\psi} = \cos \psi + i\sin \psi - \cos( -\psi) - i\sin (-\psi) = 2i\sin\psi.\]
And we have:
\[E(\xi) = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} 2i\sin\psi.\]
We substitute $\sin\alpha$ with $\frac{2\psi}{kd}$ (according to the substitution $\psi = k\frac{d}{2}\sin \alpha$) and we obtain the electric field on the screen:
\[ E(\xi) = \frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}. \tag{2}\]
Its complex conjugate is:
\[ E^\star(\xi)= \frac{E_0d}{\sqrt{l}} e^{-i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}. \tag{3}\]
Hint 3 — Light intensity on the screen
The wavefronts of the cylindrical waves can be considered planar at the far-away screen and we can calculate the intensity of the light at the screen using the formula
\[I = \frac{1}{2z_0} EE^\star.\]
Hint 3 solution — Light intensity on the screen
We substitute equations (2) and (3) into the formula for the intensity of light:
\[ I = \frac{1}{2z_0} EE^\star = \overbrace{\frac{E_0^2 d^2}{2z_0l}}^{\mathrm{def.\,}I_0} \underbrace{e^{i(\cdots)}e^{-i(\cdots)}}_{1} \frac{\sin^2 \psi}{\psi^2} = I_0 \frac{\sin^2 \psi}{\psi^2}, \]
where $\psi = k\frac{d}{2}\sin \alpha.$

$Diffraction pattern$

A very intense major maximum is located in the middle of the screen and the intensities of parallel minor maxima decrease with distance from the middle of the screen.
Hint 4 — Analysis of the diffraction pattern
Assess the width of the primary and of the minor maxima of the diffraction pattern.
Hint 4 solution — Analysis of the diffraction pattern
Let us analyze the function of the diffracted intensity:
\[I = I_0 \frac{\sin^2 \psi}{\psi^2}, \qquad \mathrm{where} \qquad I_0 = \frac{E_0^2 d^2}{2z_0l} \quad \mathrm{and}\quad \psi = k\frac{d}{2}\sin \alpha. \]
$Single-slit diffraction pattern$

The diffraction function attains its maximal value $I_0$ for $\psi = 0$ because:
\[I_0 \frac{\sin^2\psi}{\psi^2} \le I_0\frac{1}{\psi^2} \qquad \mathrm{and}\qquad \lim_{\psi \to 0} I_0 \frac{\sin^2\psi}{\psi^2} = I_0.\]
For a small value of the angle $\alpha$, there is
\[\sin \alpha \,\approx\, \tan \alpha = \frac{x}{l}.\]
The minima of the intensity of light occur for
\[ \begin{eqnarray} \psi &=& m\pi, \quad m\in \mathbb{Z}\setminus\lbrace 0 \rbrace \\ k\frac{d}{2}\sin \alpha_m &=& m\pi \\ k\frac{d}{2} \frac{x_m}{l} &=& m\pi \quad \Rightarrow \quad x_m = m\frac{2\pi l}{kd} = m\frac{\lambda l }{d}, \end{eqnarray} \]
where we have used the definition of the wave number $k=\frac{2\pi}{\lambda}$.

The width of the central stripe is
\[s = x_1 - x_{-1} = \frac{\lambda l}{d} - \left( - \frac{\lambda l}{d} \right) = \frac{2\lambda l}{d}.\]
The width of the other stripes is half since
\[s^\prime = \underbrace{x_j - x_{j-1}}_{ j \in \mathbb{Z} \setminus \lbrace 0{,}1 \rbrace } = j \frac{\lambda l}{d} - (j-1) \frac{\lambda l}{d} = \frac{\lambda l}{d}.\]
The proportions of the diffraction pattern in Fraunhofer diffraction are proportional to $\lambda l/d$.

The diffraction pattern widens with increasing distance $l$ of the screen from the slit and with increasing wavelength $\lambda$ of the diffracting light and it gets narrower/denser with increasing the width $d$ of the slit.
Solution
The contribution to the electric field on the screen at a point with coordinate $\xi$ from the elementary source of width $\mathrm d x$ located at the distance $x$ from the center of the slit is:
\[\mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{\rho}} e^{i(\omega t - k\rho)} \mathrm{d}x,\tag{4}\]
where $E_0$ is a constant ($[E_0]=\mathrm{V}\cdot\mathrm{m^{-\frac{3}{2}}}$) and $\rho$ is the ray path from the linear elementary source to the point at the screen that can be expressed using $l, \, \xi, \, x$ as follows:
\[\rho = \sqrt{l^2 + (\xi-x)^2}.\]
We implement two approximations:
1. Neglecting the decrease of amplitude across the screen:
  
  The amplitude of the electric field in (4) decreases with $\sqrt\rho$. For a screen far enough, the change of $\rho$ at various points along the $\xi$ coordinate is negligible and we approximate the variable expression $\frac{1}{\sqrt\rho}$ with the constant value $\frac{1}{\sqrt{l}}$, corresponding to the point at the optical axis. This simplifies the future integration.
2. We rearrange the expression for $\rho$ taking into account that $|x| \lt d \ll l$:
  \[\rho = \sqrt{l^2 + (\xi-x)^2} = \sqrt{l^2 + \xi^2 - 2\xi x + x^2} = \\ = \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{grey}{\frac{x^2}{l^2 + \xi^2}}}= \]
  We drop the grey fraction above as it is negligible for large $l$ with respect to the first fraction. Instead, we insert a negligibly small addition (in blue below) to complete the square of the expression inside the square root:
  \[ \begin{align} &= \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{blue}{\frac{\xi^2 x^2}{\left(l^2 + \xi^2\right)^2}}}= \\ &= \sqrt{l^2 + \xi^2}\bigg(1-\frac{\xi x}{l^2 + \xi^2} \bigg)= \\ &= \sqrt{l^2 + \xi^2}-x\overbrace{\frac{\xi}{\sqrt{l^2 + \xi^2}}}^{\sin \alpha} \\ &= \sqrt{l^2 + \xi^2} - x\sin \alpha. \end{align} \]
The approximations above give us the electric field contribution in the following shape:
\[ \mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{l}} e^{i(\omega t - k\rho)}\mathrm{d}x, \qquad \mathrm{with} \, \rho = \sqrt{l^2 + \xi^2} - x\sin \alpha. \]
The resulting electric field at the coordinate $\xi$ at the screen is given by the sum of the electric field contributions from all elementary sources over the slit width from $x=-\frac{d}{2}$ to $\frac{d}{2}$:
\[ E(\xi) = \int_\mathrm{slit}\mathrm{d}E_x(\xi) = \int_{-\frac{d}{2}}^{\frac{d}{2}} \frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x. \]
We solve this integral
\[ E(\xi) = \int_{-\frac{d}{2}}^{\frac{d}{2}} \frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x.\]
We factor out the terms independent of $x$ in front of the integral:
\[ \begin{align} E(\xi) &= \int_{-\frac{d}{2}}^{\frac{d}{2}} \frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x = \\ &= \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \int_{-\frac{d}{2}}^{\frac{d}{2}} e^{ikx\sin \alpha}\,\mathrm{d}x = \\ &= \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left[ \frac{e^{ikx\sin \alpha}}{ik\sin\alpha} \right]_{-\frac{d}{2}}^{\,\,\frac{d}{2}} = \\ &= \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left(e^{ik\frac{d}{2}\sin \alpha} - e^{-ik\frac{d}{2}\sin \alpha} \right). \end{align} \]
Let us abbreviate $\psi = k\frac{d}{2}\sin \alpha$. We separately treat the complex exponentials in the parentheses. We transform them to the trigonometric shape $(e^{i\varphi} = \cos \varphi + i \sin \varphi)$.
\[e^{i\psi} - e^{-i\psi} = \cos \psi + i\sin \psi - \cos( -\psi) - i\sin (-\psi) = 2i\sin\psi.\]
And we have:
\[E(\xi) = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} 2i\sin\psi.\]
We substitute $\sin\alpha$ with $\frac{2\psi}{kd}$ (according to the substitution $\psi = k\frac{d}{2}\sin \alpha$) and we obtain the electric field on the screen:
\[ E(\xi) = \frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}. \tag{5}\]
Its complex conjugate is:
\[ E^\star(\xi)= \frac{E_0d}{\sqrt{l}} e^{-i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}. \tag{6}\]
We substitute equations (5) and (6) into the formula for the intensity of light:
\[ I = \frac{1}{2z_0} EE^\star = \overbrace{\frac{E_0^2 d^2}{2z_0l}}^{\mathrm{def.\,}I_0} \underbrace{e^{i(\cdots)}e^{-i(\cdots)}}_{1} \frac{\sin^2 \psi}{\psi^2} = I_0 \frac{\sin^2 \psi}{\psi^2}, \]
where $\psi = k\frac{d}{2}\sin \alpha.$

$Diffraction pattern$

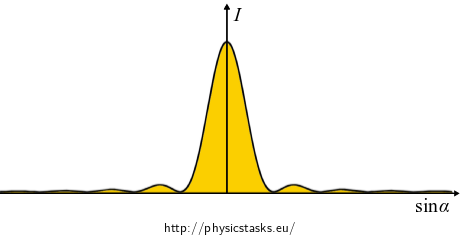
A very intense major maximum is located in the middle of the screen and the intensities of parallel minor maxima decrease with distance from the middle of the screen.

Let us analyze the function of the diffracted intensity:
\[I = I_0 \frac{\sin^2 \psi}{\psi^2}, \qquad \mathrm{where} \qquad I_0 = \frac{E_0^2 d^2}{2z_0l} \quad \mathrm{and}\quad \psi = k\frac{d}{2}\sin \alpha. \]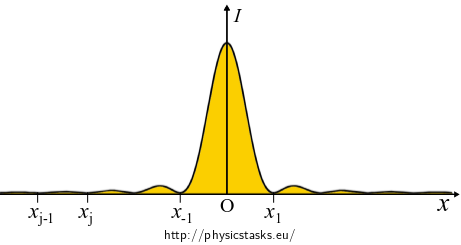
$Single-slit diffraction pattern$

The diffraction function attains its maximal value $I_0$ for $\psi = 0$ because:
\[I_0 \frac{\sin^2\psi}{\psi^2} \le I_0\frac{1}{\psi^2} \qquad \mathrm{and}\qquad \lim_{\psi \to 0} I_0 \frac{\sin^2\psi}{\psi^2} = I_0.\]
For a small value of the angle $\alpha$, there is
\[\sin \alpha \,\approx\, \tan \alpha = \frac{x}{l}.\]
The minima of the intensity of light occur for
\[ \begin{eqnarray} \psi &=& m\pi, \quad m\in \mathbb{Z}\setminus\lbrace 0 \rbrace \\ k\frac{d}{2}\sin \alpha_m &=& m\pi \\ k\frac{d}{2} \frac{x_m}{l} &=& m\pi \quad \Rightarrow \quad x_m = m\frac{2\pi l}{kd} = m\frac{\lambda l }{d}, \end{eqnarray} \]
where we have used the definition of the wave number $k=\frac{2\pi}{\lambda}$.

The width of the central stripe is
\[s = x_1 - x_{-1} = \frac{\lambda l}{d} - \left( - \frac{\lambda l}{d} \right) = \frac{2\lambda l}{d}.\]
The width of the other stripes is half since
\[s^\prime = \underbrace{x_j - x_{j-1}}_{ j \in \mathbb{Z} \setminus \lbrace 0{,}1 \rbrace } = j \frac{\lambda l}{d} - (j-1) \frac{\lambda l}{d} = \frac{\lambda l}{d}.\]
The proportions of the diffraction pattern in Fraunhofer diffraction are proportional to $\lambda l/d$.

The diffraction pattern widens with increasing distance $l$ of the screen from the slit and with increasing wavelength $\lambda$ of the diffracting light and it gets narrower/denser with increasing the width $d$ of the slit.
Answer
The intensity of light diffracted on the slit on the distant screen is described with the function
\[ I = I_0 \frac{\sin^2 \psi}{\psi^2}, \\ \mathrm{where}\qquad I_0 = \frac{E_0^2 d^2}{2z_0l}\quad \mathrm{and}\quad \psi = k\frac{d}{2}\sin \alpha. \]

The width of the central stripe is $\frac{2\lambda l}{d}$, the width of the other stripes is half.

The diffraction pattern widens with increasing distance $l$ of the screen from the slit and with increasing wavelength $\lambda$ of the diffracting light and it gets narrower/denser with increasing the width $d$ of the slit.

The figure shows a home made diffraction pattern. A laser pointer is shining on a distant wall through a vertical narrow slit between the slightly opened cutting edges of wire cutters.