What Is the Area of the Sky Seen by a Fish?
Task number: 1961
Fish is in the depth of \(3\) \(\mathrm{m}\) looking towards the surface. What is the area of the placid water surface in which the fish sees the sky?

Notation
\(h=3\) \(\mathrm{m}\) distance between the eye of the fish and the surface \(S=\) \(?\) area in which the fish sees the sky Hint 1
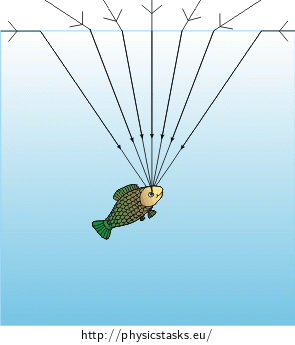
Draw the light beam travelling from the air to the surface and then to the fish’s eye.
Hint 2
What is the shape of the area in which the fish sees the sky?
Hint 3
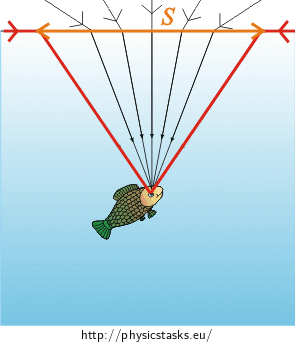
In the „Travelling beams“ picture, contained it the section „Solution of Hint \(1\)“, keep only those rays which are refracted to the eye.
Mark the rays in the picture between which the angle is the largest. These rays circumscribe the desired area \(S\). Provide reasoning why.
Hint 4
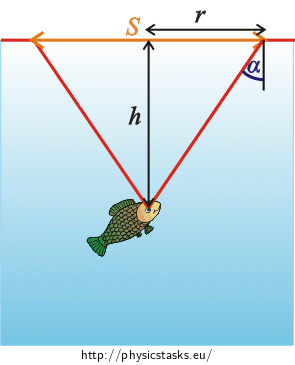
Now we focus only on the beams that are refracted at the angle \(\mathrm{α}\), see „Picture to Hint 4“.
We mark the radius of the desired areay \(r\) and the distance from the fish’s eye to the surface \(h\).
1) Write the relation for the angle \(\mathrm{α}\) in accordance with the law of refraction.2) Deduce the relation between \(\mathrm{α}\), \(r\) and \(h\) from the picture.Hint 5
Express the radius \(r\) from relation (3) and adjust the obtained equation using the relation acquired from the law of refraction (2), so that \(r\) depends only on \(h\), \(n_{1}\) and \(n_{2}\).
Then substitute \(r\) in the relation for calculating area of the circle (1) and compute the value of the desired area numerically.
Overall Solution
Trajectory of the light beams and the shape of the area in which the fish sees the sky
We assume the fish’s eye as the point in which the rays converge.
The area will be circular with the radius \(r\): \[S=\pi · r^2.\tag{1}\]
The beams which are incident on the surface at the angle of \(\mathrm{90°}\)
Now we focus only on the beams that are refracted at the angle \(\mathrm{α}\) (see „Picture of the beams“).
We derive the relation for the angle of refraction \(\mathrm{α}\) from Snell’s law: \[\frac{\sin {90°}}{\sin \mathrm{α}}=\frac{n_{2}}{n_{1}},\] where \(n_{1}\) is the refractive index of air and \(n_{2}\) is the refractive index of water.
Since \(\sin {90°}=1\), we can write:
\[\frac{1}{\sin \mathrm{α}}=\frac{n_{2}}{n_{1}},\]Therefrom we express \(\sin \mathrm{α}\):
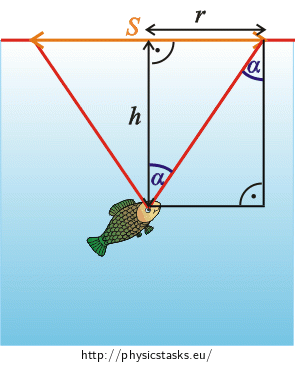
\[\sin \mathrm{α}=\frac{n_{1}}{n_{2}},\tag{2}\]Due to the similarity of triangles we can adjust the picture as follows:
We can see from the picture that \[\sin \mathrm{α}=\frac{r}{\sqrt{r^2+h^2}},\tag{3}\] where \(\sqrt{r^2+h^2}\) is a hypotenuse of the triangle and we have determined its length from the Pythagorean theorem.
Size of the desired area
(1): \(S=\pi · r^2,\)
(2): \(\sin \mathrm{α}=\frac{n_{1}}{n_{2}},\)
(3): \(\sin \mathrm{α}=\frac{r}{\sqrt{r^2+h^2}}.\)
If we multiply both sides of the equation (3) by \(\sqrt{r^2+h^2}\), we will obtain: \[r=\sqrt{r^2+h^2}·\sin \mathrm{α}.\]
According to (2)) we substitute \(\sin \mathrm{α}\): \[r= \sqrt{r^2+h^2} · \frac{n_{1}}{n_{2}}.\]
We raise both sides of the equation to the power of two and multiply the brackets:
\[r^2= \left(r^2+h^2 \right)· \left(\frac{n_{1}}{n_{2}}\right)^2=r^2\left(\frac{n_{1}}{n_{2}}\right)^2+h^2\left(\frac{n_{1}}{n_{2}}\right)^2 .\]
Then we subtract \(r^2\left (\frac{n_{1}}{n_{2}}\right )^2\) from both sides of the equation and factor out \(r^2\): \[r^2\left [1 − \left(\frac{n_{1}}{n_{2}}\right)^2\right]= h^2\left (\frac{n_{1}}{n_{2}}\right)^2 .\]
We divide both sides of the equation by \(\left[1 − (\frac{n_{1}}{n_{2}})^2\right]\) and extract the root: \[r= \frac {h\left(\frac{n_{1}}{n_{2}}\right)} {\sqrt{1 − \left(\frac{n_{1}}{n_{2}}\right)^2}}= \frac {h · n_{1}} {n_{2} \sqrt{1 − \left(\frac{n_{1}}{n_{2}}\right)^2}} .\]
We convert the expression inside the square root to the common denominator and adjust the fraction: \[r= \frac {h · n_{1}} {n_{2} \sqrt{\frac{n_{2}^2−n_{1}^2}{n_{2}^2}}} =\frac {h · n_{1}} { \sqrt{n_{2}^2−n_{1}^2}}.\]
We substitute \(r\) in relation (1) and raise the whole equation to the power of two: \[S=\pi r^2=\pi · \left( \frac {h · n_{1}} {\sqrt{n_{2}^2−n_{1}^2}}\right)^2= \pi · \frac {h^2 · n_{1}^2} {n_{2}^2−n_{1}^2} .\]
Numerical solution:
We know from the task assignment:
\(h=3\) \(\mathrm{m}\).
We look up the values of \(\pi\), \(n_{2}\) a \(n_{1}\) in the Tables:
Ludolph’s number \(\pi\) \(\dot=\) \(3{.}14\) Refractive index of air \(n_{1}\) \(\dot=\) \(1{.}00\) Refractive index of water \(n_{2}\) \(\dot=\) \(1{.}33\) We substitute for the values and obtain the size of the desired area:
\(S\) \(\dot=\) \(\frac{3{.}14 · 3^2 ·{1{.}00}^2}{{1{.}33}^2 − {1{.}00}^2}\) \(\mathrm{m^2}=\frac{3{.}14 · 9 ·1}{{1{.}33}^2 − {1}}\) \(\mathrm{m^2}\) \(\dot=\) \(36{.}8\) \(\mathrm{m^2}\)and its radius:
\(r\) \(\dot=\) \( \frac {3 · 1{.}00} {\sqrt{1{.}33^2 −1{.}00^2}}\) \(\mathrm{m}\) \(=\) \( \frac {3} {\sqrt{1{.}33^2 − 1}}\) \(\mathrm{m}\) \(\dot=\) \(3{.}42\) \(\mathrm{m}\).Answer
The fish sees the sky in the circular area of \(36{.}8\) \(\mathrm{m^2}\) with the radius of \(3{.}42\) \(\mathrm{m}\).