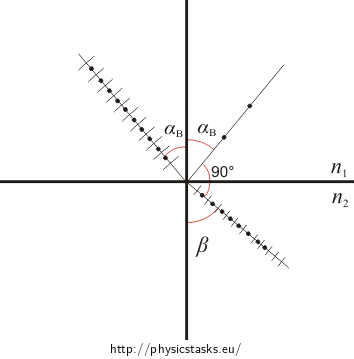Collection of Solved Problems in Physics

Polarization by Total Internal Reflection

Task number: 2329

• Hint 1

  How does the polarization by reflection work and which relation holds for Brewster’s angle of incidence?

• Hint 1 solution

  If the unpolarized light is incident on a boundary of two media, it is partially reflected and partially refracted. When the reflected and refracted rays form an angle of 90°, the reflected angle is completely polarized. The angle of incidence is then called Brewster’s angle α_B and it is dependent on the index of refraction of the medium.

  Note: the reflected ray is polarised perpendicular to the plane of incidence.

  

  The direction of oscillation in the plane perpendicular to the plane of incidence is marked by dots and the direction of oscillation in the plane of incidence by small line segments.

  If the reflected and refracted rays form an angle of 90° we can see from the image that:

  \[\alpha_\mathrm{B}+ 90° + \beta = 180°.\]

  Simplifying we get:

  \[\beta = 90° − \alpha_\mathrm{B}. \]

  Modifying the Snell’s law, we get:

  \[\frac{\sin\, \alpha_\mathrm{B}}{\sin\, \beta}=\frac{n_\mathrm{2}}{n_\mathrm{1}}.\]

  We substitute for β:

  \[\frac{\sin\, \alpha_\mathrm{B}}{\sin\,(90° - \alpha_\mathrm{B})}=\frac{n_\mathrm{2}}{n_\mathrm{1}}.\]

  Using the equality sin(90° − α) = cos α we rewrite the expression:

  \[\frac{\sin\, \alpha_\mathrm{B}}{\cos\,\alpha_\mathrm{B}}=\mathrm{tg}\,\, \alpha_\mathrm{B}=\frac{n_\mathrm{2}}{n_\mathrm{1}}\]

  and get the relation for dependence of the Brewster’s angle α_B on the indices of refraction of the two media.

• Solution

  The light must come under a particular angle of incidence, so called Brewster’s angle α_B, to be reflected with complete polarization. At this angle reflected and refracted rays form an angle of 90°. We can get the following relation:

  \[\alpha_\mathrm{B}+ 90° + \beta = 180°.\]

  For detailed derivation see the Hint 1 solution.

  Simplifying we get:

  \[\beta = 90° − \alpha_\mathrm{B}. \]

  Modifying the Snell’s law, we get:

  \[\frac{\sin\, \alpha_\mathrm{B}}{\sin\, \beta}=\frac{\sin\, \alpha_\mathrm{B}}{\sin\,(90° − \alpha_\mathrm{B})}=\frac{\sin\, \alpha_\mathrm{B}}{\cos\,\alpha_\mathrm{B}}=\mathrm{tg}\,\, \alpha_\mathrm{B}= \frac{n_\mathrm{2}}{n_\mathrm{1}}.\]

  As the task assignment did not mention differently, we assume that the problem is happening in vacuum or in air, so we can substitute for n₁ = 1.

  \[\mathrm{tg}\,\, \alpha_\mathrm{B}= \frac{n_\mathrm{2}}{1},\]

  Thus:

  \[\mathrm{tg}\,\, \alpha_\mathrm{B}= n_\mathrm{2}.\]

  We can substitute for the Brewster’s angle α_B = 58° from the assignment and calculate the index of refraction of enamel:

  \[n_\mathrm{2}=\mathrm{tg}\,\,58°\dot=\,1{,}6.\]

  We can also calculate Brewster’s angle for diamond with the index of refraction n₂ = 2,42:

  \[\mathrm{tg}\,\, \alpha_\mathrm{B}= n_\mathrm{2} = 2{,}42,\] \[\alpha_\mathrm{B} \dot=\,68°.\]

• Answer

  The index of refraction of enamel is n = 1,6 and the polarization angle of diamond is α_B = 68°.