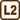Position of First–Order Maxima When Two Coherent Rays Interfere
Task number: 1699
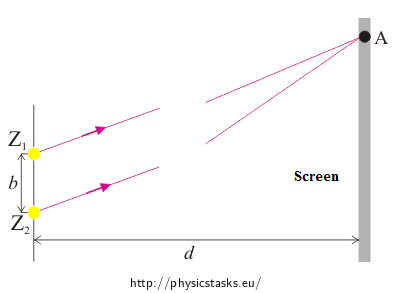
The distance between two coherent light sources is 0.45 mm. Determine the distance between the zero-order maximum and the first red stripe of a wavelength 700 nm, provided that the screen is at a distance 0.5 m from the sources.
Hint 1
What is the path difference of two rays which are emitted from two sources and incident on the same point of the screen?
Hint 2
What is the path difference of two rays in order to create an interference maximum?
Hint 3
What is the relationship between the distance of the first red maximum Δx,which occurs on the screen, and the angle of deflection α?
Given values
b = 0.45 mm = 4.5·10−4 m Distance between two light sources λ = 700 nm = 7.0·10−7 m Wavelength of light k = 1 Order of maximum d = 0.5 m Distance between the sources and the screen Δx = ? (mm) Distance between the first-order red maximum and the zero-order maximum Solution
The light propagates from its source in all directions. The light from both sources is incident on the screen, and an interference pattern is created. On the screen the interference maxima and minima are formed; their position depends on the path difference of the two rays emitted from the sources.
Suppose that the screen is far from the sources, so that the rays coming to a point A of the screen are approximately parallel.
From the triangle in the picture we obtain a relationship for the path difference Δl of two adjacent rays::
\[\mathrm{\Delta}l = \,b\sin\,\alpha,\]where b is the distance between the sources and α is the angle between the rays and the central axis.
In the point A the rays interfere and create a stripe, a maximum. Thus the path difference Δl must satisfy the condition:
\[\mathrm{\Delta}l = k \lambda,\]where k = 1. From these two equations we evaluate sin α:
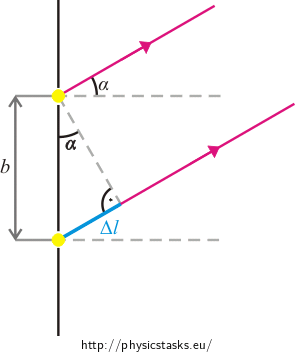
\[\sin\,\alpha=\,\frac{\lambda}{b}.\]We draw a picture where we denote d as the distance between the sources and the screen, α as deviation angle, Δx as the distance between the first-order red maximum and the zero-order maximum.
We obtain:
\[\mathrm{tg}\,\,\alpha=\, \frac{\mathrm{\Delta}x}{d} \quad\Rightarrow\quad \mathrm{\Delta}x=\,d\,\mathrm{tg}\,\,\alpha,\]where α is calculated from the relation:
\[\sin\,\alpha=\,\frac{\lambda}{b}=\,\frac{7.0{\cdot}10^{−7}}{4.5{\cdot}10^{−4}}\,\dot=\,0.00156 \quad\Rightarrow\quad \alpha\,\dot=\,0.00156,\]and we substitute the values given in the assignment.
\[\mathrm{\Delta}x=\,d\,\mathrm{tg}\,\,\alpha=\,0.5\,\cdot(\mathrm{tg}\,\,0.00156)\,\mathrm{m}\,\dot=\, 8.0{\cdot}10^{−4}\,\mathrm{m}\,\dot= \,0.80\,\mathrm{mm}. \]Note to the solution:
To simplify the calculation we can take into account that we deal with very small angles, therefore
\[\sin\,\alpha\ \dot{=}\ \, \alpha\ \dot{=}\ \mathrm{tg}\,\,\alpha,\]where the middle equality is valid if the angle α is in radians.
Now we solve this task using this finding.
We substitute the relation:
\[\sin\,\alpha=\,\frac{\lambda}{b},\]into the equation for Δx:
\[\mathrm{\Delta}x=\,d\,\mathrm{tg}\,\,\alpha=\,d\,\frac{\lambda}{b}.\]We substitute given values.
\[\mathrm{\Delta}x=\,d\,\frac{\lambda}{b}=\,0.5\cdot\,\frac{7.0{\cdot}10^{−7}}{4.5{\cdot}10^{−4}}\,\mathrm{m}\,\dot=\,7.8{\cdot}10^{−4}\,\mathrm{m}\,\dot=\,0.78\,\mathrm{mm}.\]Thus we can see that the task can be solved with this neglect. This result is not very different from the first result.
Answer
The first red stripe appears approximately 0.8 mm from the zero-order maximum.
Link to experiment
If you would like to see the interference pattern created on the screen, look at the Double-Slit Experiment.